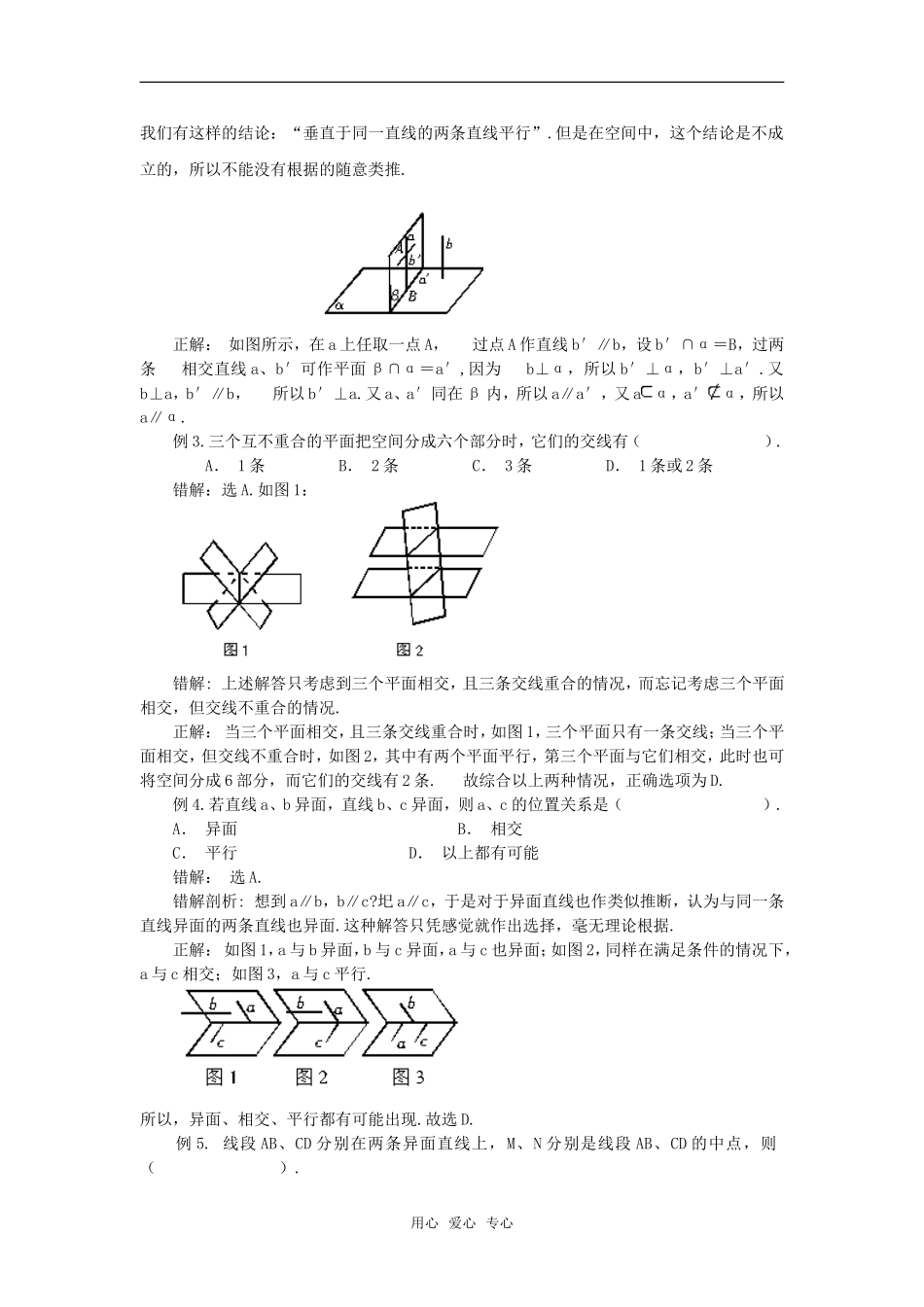
空间位置关系错中“悟”我们这里所说的空间中位置关系主要包括线线、线面及面面关系,它们是学习立体几何的基础,由于该部分内容比较多,初学者的空间观念还没有建立起来,所以经常出现解题失误.特举例如下:例1.求证:四个角都是直角的四边形是矩形.错解:∵四边形的四个角都是直角,∴其内角和为360°.∴此四边形为平面四边形,从而得到该四边形为矩形.错解剖析:在上述的证明过程中,我们看到由“内角和为360°”就直接推出“四边形为平面四边形”进而推出最终结论,这样的理由是不充分的,所以亮起了红灯.正解:我们看到题目给出的条件很简单,只有一个“四个角都是直角的四边形”,那么我们要想,这个四边形是平面的还是空间的?如果是平面四边形,很容易得到它是矩形,但如果是空间四边形,是否结论还成立呢?下面我们通过反证法来证明.(反证法)假设四边形ABCD是空间四边形,且四个内角都是直角,如图,过D作DE∥AB,则AD⊥DE,AD⊥DC,BC⊥DC,BC⊥DE.设两条相交直线DE、DC确定的平面为α,则AD⊥α,BC⊥α.∴根据“如果两条直线同垂直于一个平面,那么这两条直线平行.”有AD∥BC,∴AD、BC共面,这与假设ABCD是空间四边形相矛盾.∴四边形ABCD是平面四边形.从而得到该四边形为矩形.例2.已知aα,a⊥b,b⊥α,求证:a∥α.错解:因为b⊥α,a⊥b,所以aα或a∥α.又aα,所以a∥α.错解剖析:上面解题过程被亮起红灯的原因是对位置关系的判定理解不正确.在平面里,用心爱心专心我们有这样的结论:“垂直于同一直线的两条直线平行”.但是在空间中,这个结论是不成立的,所以不能没有根据的随意类推.正解:如图所示,在a上任取一点A,过点A作直线b′∥b,设b′∩α=B,过两条相交直线a、b′可作平面β∩α=a′,因为b⊥α,所以b′⊥α,b′⊥a′.又b⊥a,b′∥b,所以b′⊥a.又a、a′同在β内,所以a∥a′,又aα,a′α,所以a∥α.例3.三个互不重合的平面把空间分成六个部分时,它们的交线有().A.1条B.2条C.3条D.1条或2条错解:选A.如图1:错解:上述解答只考虑到三个平面相交,且三条交线重合的情况,而忘记考虑三个平面相交,但交线不重合的情况.正解:当三个平面相交,且三条交线重合时,如图1,三个平面只有一条交线;当三个平面相交,但交线不重合时,如图2,其中有两个平面平行,第三个平面与它们相交,此时也可将空间分成6部分,而它们的交线有2条.故综合以上两种情况,正确选项为D.例4.若直线a、b异面,直线b、c异面,则a、c的位置关系是().A.异面B.相交C.平行D.以上都有可能错解:选A.错解剖析:想到a∥b,b∥c?圯a∥c,于是对于异面直线也作类似推断,认为与同一条直线异面的两条直线也异面.这种解答只凭感觉就作出选择,毫无理论根据.正解:如图1,a与b异面,b与c异面,a与c也异面;如图2,同样在满足条件的情况下,a与c相交;如图3,a与c平行.所以,异面、相交、平行都有可能出现.故选D.例5.线段AB、CD分别在两条异面直线上,M、N分别是线段AB、CD的中点,则().用心爱心专心错解:想到梯形的中位线定理,故选C.错解剖析:由于四边形ABDC是空间四边形,不满足梯形的中位线定理,从而出错.正解:如下图所示,四边形ABDC是空间四边形,而不是平面四边形,要想求MN与AB、CD的关系,必须将它们转化到平面来考虑.我们可以连结AD,取AD的中点为G,再连结MG、NG,如图:在△ABD中,M、G分别是线段AB、AD的中点,则MG∥BD,且,同理,在△ADC中,NG∥AC,且,又根据三角形的三边关系知,MN