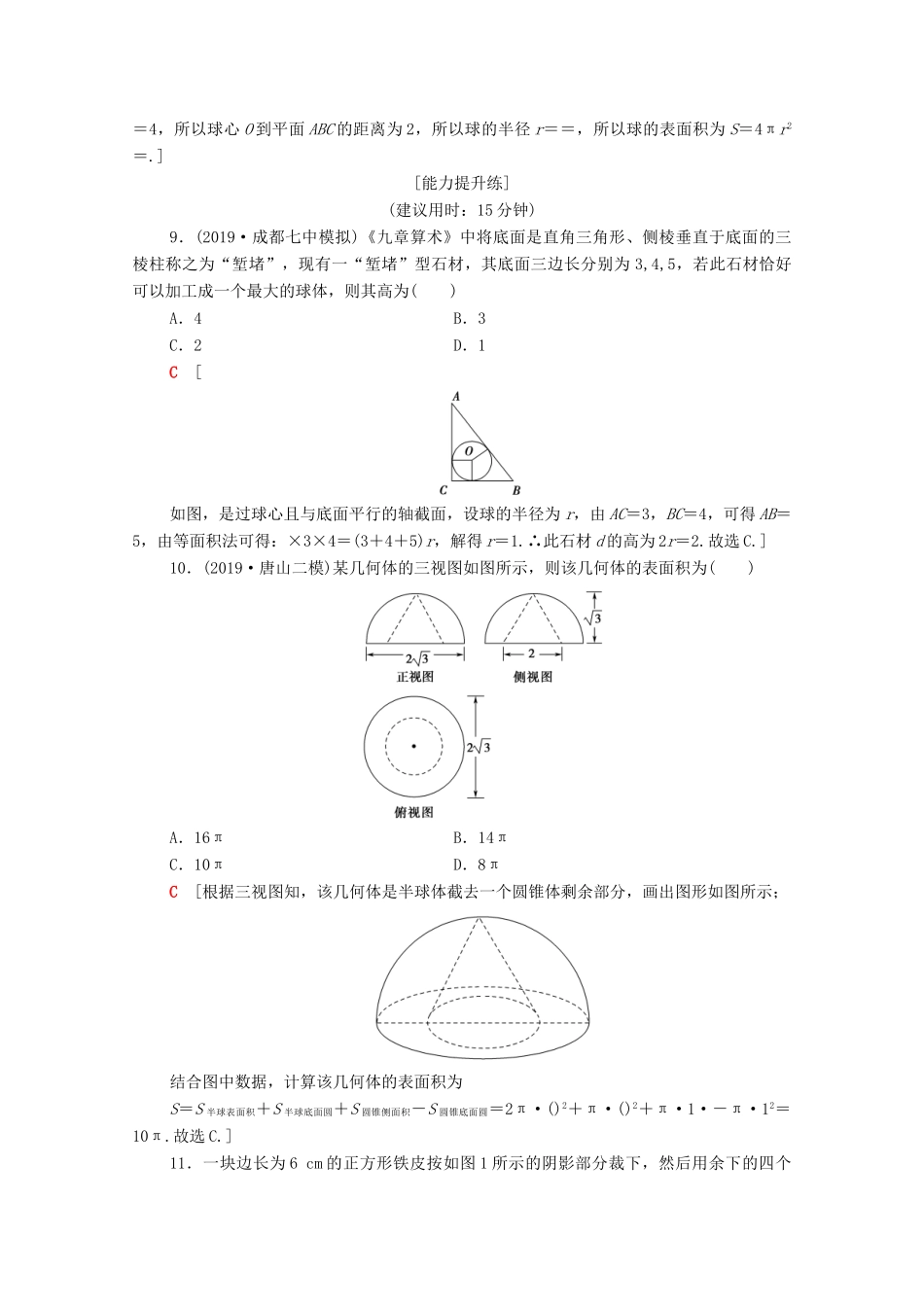
专题限时集训(七)空间几何体的表面积、体积及有关量的计算[专题通关练](建议用时:30分钟)1.在一个密闭透明的圆柱筒内装一定体积的水,将该圆柱筒分别竖直、水平、倾斜放置时,指出圆柱桶内的水平面可以呈现出的几何形状不可能是()A.圆面B.矩形面C.梯形面D.椭圆面或部分椭圆面C[将圆柱桶竖放,水面为圆面;将圆柱桶斜放,水面为椭圆面或部分椭圆面;将圆柱桶水平放置,水面为矩形面,所以圆柱桶内的水平面可以呈现出的几何形状不可能是梯形面,故选C.]2.[易错题]一个正方体的内切球O1、外接球O2、与各棱都相切的球O3的半径之比为()A.1∶3∶2B.1∶1∶1C.1∶∶D.1∶2∶3C[设正方体的棱长为1,则其内切球O1的半径为,外接球O2的半径为(正方体体对角线的一半),与各棱都相切的球O3的半径为(正方体面对角线的一半),所以它们的半径之比是1∶∶,故选C.]3.已知三棱锥PABC中,PB⊥平面ABC,∠ABC=90°,PA=,AB=BC=1,则三棱锥P-ABC的外接球的表面积为()A.12πB.6πC.24πD.B[如图, PB⊥平面ABC,∴PB⊥AB, AB=1,PA=,∴PB=2,又AB⊥BC,把三棱锥PABC补形为长方体,则长方体对角线长为=,则三棱锥PABC外接球的半径为,∴三棱锥PABC的外接球的表面积为4π×=6π.故选B.]4.[重视题]两个相同的正四棱锥底面重合组成一个八面体,可放于棱长为1的正方体中,重合的底面与正方体的某一个面平行,各顶点均在正方体的表面上(如图),该八面体的体积可能值有()A.1个B.2个C.3个D.无数个D[设ABCD与正方体的截面四边形为A′B′C′D′,设AA′=x(0≤x≤1),则AB′=1-x,|AD|2=x2+(1-x)2=2+,故S四边形ABCD=|AD|2∈,V=S四边形ABCD·h·2=S四边形ABCD∈.∴该八面体的体积可能值有无数个,故选D.]5.已知正三棱柱ABCA1B1C1的底面边长为2,侧棱长为,D为BC的中点,则三棱锥A-B1DC1的体积为()A.3B.C.1D.C[ D是等边三角形ABC的边BC的中点,∴AD⊥BC.又ABCA1B1C1为正三棱柱,∴AD⊥平面BB1C1C. 四边形B为矩形,∴S=S=×2×=.又AD=2×=,∴V=S·AD=××=1.故选C.]6.如图所示,图中阴影部分绕AB旋转一周所形成的几何体的体积为________.[由题知,旋转一周后形成的几何体是一圆台去掉一个半球,其中圆台的体积为V=×(π×22++π×52)×4=52π,半球的体积V=××π×23=,则所求体积为52π-=.]7.鲁班锁是中国传统的智力玩具,起源与古代汉族建筑中首创的榫卯结构,这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合,十分巧妙,外观看是严丝合缝的十字立方体,其上下、左右、前后完全对称.从外表上看,六根等长的正四棱柱体分成三组,经90°榫卯起来,如图,若正四棱柱体的高为6,底面正方形的边长为1,现将该鲁班锁放进一个球形容器内,则该球形容器的表面积的最小值为________.(容器壁的厚度忽略不计)41π[由题意,该球形容器的半径的最小值为:=,∴该球形容器的表面积的最小值为4π·=41π.]8.三棱锥PABC的四个顶点均在同一个球面上,其中PA⊥平面ABC,△ABC是正三角形,PA=2BC=4,则该球的表面积为________.[球心应位于过正三角形ABC的中心且垂直于平面ABC的直线上,又PA⊥平面ABC,PA=4,所以球心O到平面ABC的距离为2,所以球的半径r==,所以球的表面积为S=4πr2=.][能力提升练](建议用时:15分钟)9.(2019·成都七中模拟)《九章算术》中将底面是直角三角形、侧棱垂直于底面的三棱柱称之为“堑堵”,现有一“堑堵”型石材,其底面三边长分别为3,4,5,若此石材恰好可以加工成一个最大的球体,则其高为()A.4B.3C.2D.1C[如图,是过球心且与底面平行的轴截面,设球的半径为r,由AC=3,BC=4,可得AB=5,由等面积法可得:×3×4=(3+4+5)r,解得r=1.∴此石材d的高为2r=2.故选C.]10.(2019·唐山二模)某几何体的三视图如图所示,则该几何体的表面积为()A.16πB.14πC.10πD.8πC[根据三视图知,该几何体是半球体截去一个圆锥体剩余部分,画出图形如图所示;结合图中数据,计算该几何体的表面积为S=S半球表面积+S半球底面圆+S圆锥侧面积-S圆锥底面圆=2π·()2+π·()2+π·1·-π·12=10π.故选C.]11.一块...