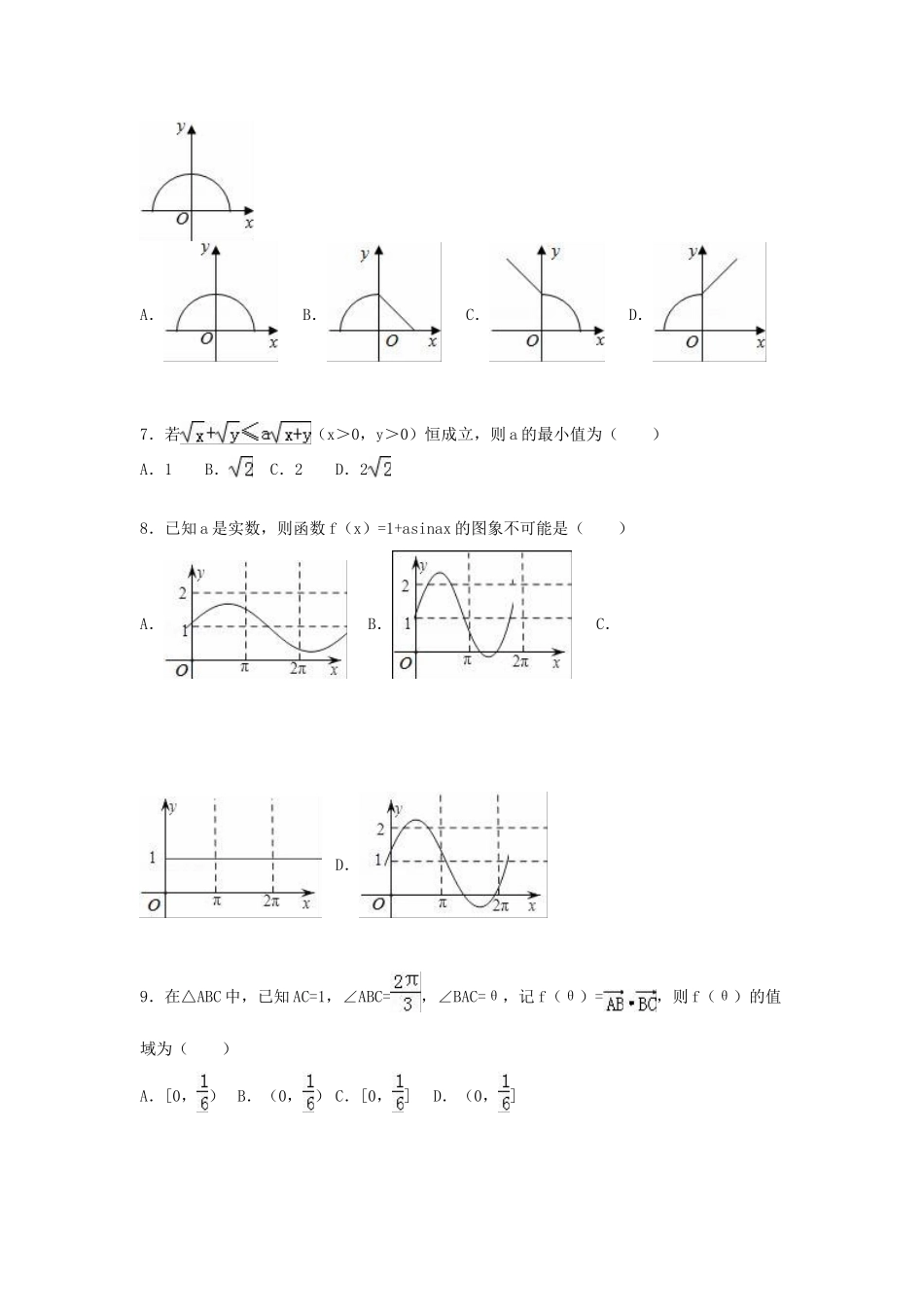
2015-2016学年河南省南阳市高三(上)期中数学试卷(理科)一、选择魔:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个是符合题目要求的.1.若集合A={x|x=in,n∈N+}(i是虚数单位),B={1,﹣1},则A∩B等于()A.{﹣1}B.{1}C.∅D.{1,﹣1}2.设复数z=(x﹣1)+yi(x∈R,y≥0),若|z|≤1,则y≥x的概率为()A.B.C.D.3.下列命题中正确的结论个数是()①“p且q为真”是“p或q为真”的必要不充分条件②命题“若ab=0,则a=0或b=0”的否命题是“若ab≠0,则a≠0且b≠0”③∃x0∈R,使.A.0B.1C.2D.34.设函数f(x)=ln(1+|x|)﹣,则使得f(x)>f(2x﹣1)成立的x的取值范围是()A.(,1)B.∪(1,+∞)C.()D.(﹣∞,,+∞)5.已知等比数列{an}满足an>0,n=1,2,…,且a5•a2n﹣5=22n(n≥3),则当n≥1时,log2a1+log2a3+…+log2a2n﹣1=()A.n(2n﹣1)B.(n+1)2C.n2D.(n﹣1)26.已知函数y=f(﹣|x|)的图象如图所示,则函数y=f(x)的图象不可能是()A.B.C.D.7.若(x>0,y>0)恒成立,则a的最小值为()A.1B.C.2D.28.已知a是实数,则函数f(x)=1+asinax的图象不可能是()A.B.C.D.9.在△ABC中,已知AC=1,∠ABC=,∠BAC=θ,记f(θ)=,则f(θ)的值域为()A.[0,)B.(0,)C.[0,]D.(0,]10.函数f(x)=,若函y=f(x)十f(2﹣x)﹣b,b∈R恰4个零,则b的取值范围是()A.(,+∞)B.(一∞,)C.(0,)D.(,2)11.已知⊥,||=,||=t,t∈[,4];若P是△ABC所在平面内一点,且=+,则的取值范围是()A.[13,17]B.[12,13]C.[,12]D.[,13]12.已知函数f(x)对任意的x∈R都满足f(x)+f(﹣x)=0,当x≥0时,f(x)=,(a>0),若对∀x∈R,都有f(x﹣2)≤f(x),则实数a的取值范围为()A.(0,)B.[,]C.(0,]D.(0,)二、填空题:本大题共4小题,每小题5分,共20分.13.若锐角△ABC的面积为,且AB=5,AC=8,则BC等于.14.已知f(x)在R上可导,且满足(x﹣2)f′(x)≥0,则f(﹣2015)+f(填两个数值的大小关系:>、=、<、≥、≤).15.设实数x,y满足约束条件,若目标函数z=+(a>0,b>0)的最大值为9,则d=的最小值为.16.设函数f(x)=若f(x)恰有2个零点,则实数a的取值范围.三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.17.在锐角△ABC中,a、b、c分别为角A、B、C所对的边,且=2csinA(1)确定角C的大小;(2)若c=,且△ABC的面积为,求a+b的值.18.Sn为数列{an}的前n项和,已知Sn=.(1)求数列{an}的通项公式;(2)若数列{bn}满足anbn=log3an,求数列{bn}的前n项和Tn.19.设f(x)是一个二次项系数为正的二次函数,f(x+3)=f(﹣1﹣x)对任意x∈R都成立,若向量=(,2sinx),=(2,sinx),=(2,1),=(1,cos2x),求f(•)﹣f(•)>0的解集.20.数列{an}的首项al=1,且对任意n∈N*,an与an+1恰为方程x2﹣bnx+2n=0的两个根.(1)求数列(an}和数列{bn}的通项公式;(2)求数列{bn}的前n项和Sn.21.已知函数f(x)=x3﹣3x.(1)求函数f(x)的极值;(2)过点P(1,n)(n≠﹣2)作曲线y=f(x)的切线,问:实数n满足什么样的取值范围,过点P可以作出三条切线?22.已知函数g(x)=x2﹣2x1nx.(1)讨论g(x)的单调性;(2)证明:存在a∈(0,1),使得g(x)≥2a(lnx+x+a﹣)(a>0)在区间(1,+∞)内恒成立,且g(x)=2a(lnx+x+a﹣)(a>0)在(1,+∞)内有唯一解.2015-2016学年河南省南阳市高三(上)期中数学试卷(理科)参考答案与试题解析一、选择魔:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个是符合题目要求的.1.若集合A={x|x=in,n∈N+}(i是虚数单位),B={1,﹣1},则A∩B等于()A.{﹣1}B.{1}C.∅D.{1,﹣1}【考点】虚数单位i及其性质.【专题】计算题;方程思想;综合法;集合;数系的扩充和复数.【分析】求出集合A,然后求解交集即可.【解答】解:集合A={x|x=in,n∈N+}(i是虚数单位),可得A={i,﹣1,﹣i,1}.B={1,...