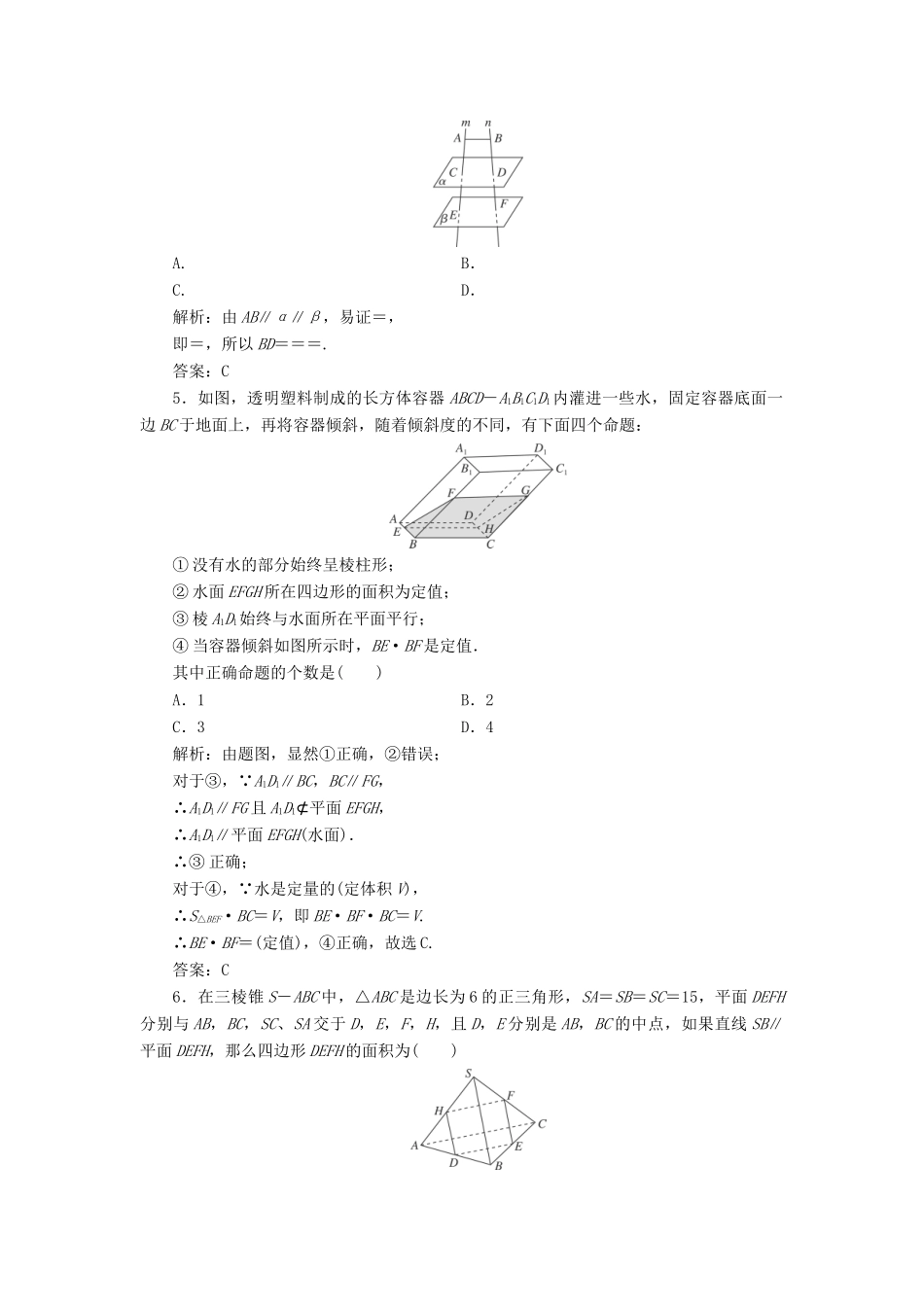
7.4直线、平面平行的判定及其性质[课时跟踪检测][基础达标]1.在空间内,下列命题正确的是()A.平行直线的平行投影重合B.平行于同一直线的两个平面平行C.垂直于同一平面的两个平面平行D.垂直于同一平面的两条直线平行解析:对于A,平行直线的平行投影也可能互相平行,或为两个点,错误;对于B,平行于同一直线的两个平面也可能相交,错误;对于C,垂直于同一平面的两个平面也可能相交,错误;而D为直线和平面垂直的性质定理,正确.答案:D2.如图所示,在空间四边形ABCD中,E,F分别为边AB,AD上的点,且AE∶EB=AF∶FD=1∶4,又H,G分别为BC,CD的中点,则()A.BD∥平面EFGH,且四边形EFGH是矩形B.EF∥平面BCD,且四边形EFGH是梯形C.HG∥平面ABD,且四边形EFGH是菱形D.EH∥平面ADC,且四边形EFGH是平行四边形解析:由AE∶EB=AF∶FD=1∶4知EF綊BD,所以EF∥平面BCD.又H,G分别为BC,CD的中点,所以HG綊BD,所以EF∥HG且EF≠HG.所以四边形EFGH是梯形.答案:B3.(2017届江西赣中南五校模拟)已知m,n是两条不同的直线,α,β,γ是三个不同的平面,则下列命题中正确的是()A.若α⊥γ,α⊥β,则γ∥βB.若m∥n,m⊂α,n⊂β,则α∥βC.若m∥n,m⊥α,n⊥β,则α∥βD.若m∥n,m∥α,则n∥α解析:对于A,若α⊥γ,α⊥β,则γ与β平行或相交;对于B,若m∥n,m⊂α,n⊂β,则α与β平行或相交;对于D,若m∥n,m∥α,则n∥α或n在平面α内.答案:C4.如图,AB∥平面α∥平面β,过A,B的直线m,n分别交α,β于C,E和D,F,若AC=2,CE=3,BF=4,则BD的长为()A.B.C.D.解析:由AB∥α∥β,易证=,即=,所以BD===.答案:C5.如图,透明塑料制成的长方体容器ABCD-A1B1C1D1内灌进一些水,固定容器底面一边BC于地面上,再将容器倾斜,随着倾斜度的不同,有下面四个命题:①没有水的部分始终呈棱柱形;②水面EFGH所在四边形的面积为定值;③棱A1D1始终与水面所在平面平行;④当容器倾斜如图所示时,BE·BF是定值.其中正确命题的个数是()A.1B.2C.3D.4解析:由题图,显然①正确,②错误;对于③, A1D1∥BC,BC∥FG,∴A1D1∥FG且A1D1⊄平面EFGH,∴A1D1∥平面EFGH(水面).∴③正确;对于④, 水是定量的(定体积V),∴S△BEF·BC=V,即BE·BF·BC=V.∴BE·BF=(定值),④正确,故选C.答案:C6.在三棱锥S-ABC中,△ABC是边长为6的正三角形,SA=SB=SC=15,平面DEFH分别与AB,BC,SC、SA交于D,E,F,H,且D,E分别是AB,BC的中点,如果直线SB∥平面DEFH,那么四边形DEFH的面积为()A.B.C.45D.45解析:取AC的中点G,连接SG,BG.易知SG⊥AC,BG⊥AC,且SG∩BG=G,故AC⊥平面SGB,所以AC⊥SB.因为SB∥平面DEFH,SB⊂平面SAB,平面SAB∩平面DEFH=HD,则SB∥HD.同理SB∥FE.又D,E分别为AB,BC的中点,则H,F也为AS,SC的中点,从而得HF綊AC綊DE,所以四边形DEFH为平行四边形.又AC⊥SB,SB∥HD,DE∥AC,所以DE⊥HD,所以四边形DEFH为矩形,其面积S=HF·HD=AC·SB=.答案:A7.如图,正方体ABCD-A1B1C1D1中,AB=2,点E为AD的中点,点F在CD上.若EF∥平面AB1C,则线段EF的长度等于________.解析:因为EF∥平面AB1C,EF⊂平面ABCD,平面ABCD∩平面AB1C=AC,所以EF∥AC,所以F为DC中点.故EF=AC=.答案:8.如图,在空间四边形ABCD中,M∈AB,N∈AD,若=,则直线MN与平面BDC的位置关系是________.解析:在平面ABD中,=,所以MN∥BD.又MN⊄平面BCD,BD⊂平面BCD,所以MN∥平面BCD.答案:平行9.在棱长为2的正方体ABCD-A1B1C1D1中,P是A1B1的中点,过点A1作与截面PBC1平行的截面,所得截面的面积是________.解析:如图,取AB,C1D1的中点E,F,连接A1E,A1F,EF,则平面A1EF∥平面BPC1.在△A1EF中,A1F=A1E=,EF=2,S△A1EF=×2×=.从而所得截面面积为2S△A1EF=2.答案:210.设α,β,γ是三个不同的平面,a,b是两条不同的直线,有下列三个条件:①a∥γ,b⊂β;②a∥γ,b∥β;③b∥β,a⊂γ.如果命题“α∩β=a,b⊂γ,且________”,则“a∥b”为真命题,则可以在横线处填入的条件是________(把所有正确条件的序号都...