高考数学复习点拨 集合对简易逻辑注释VIP免费

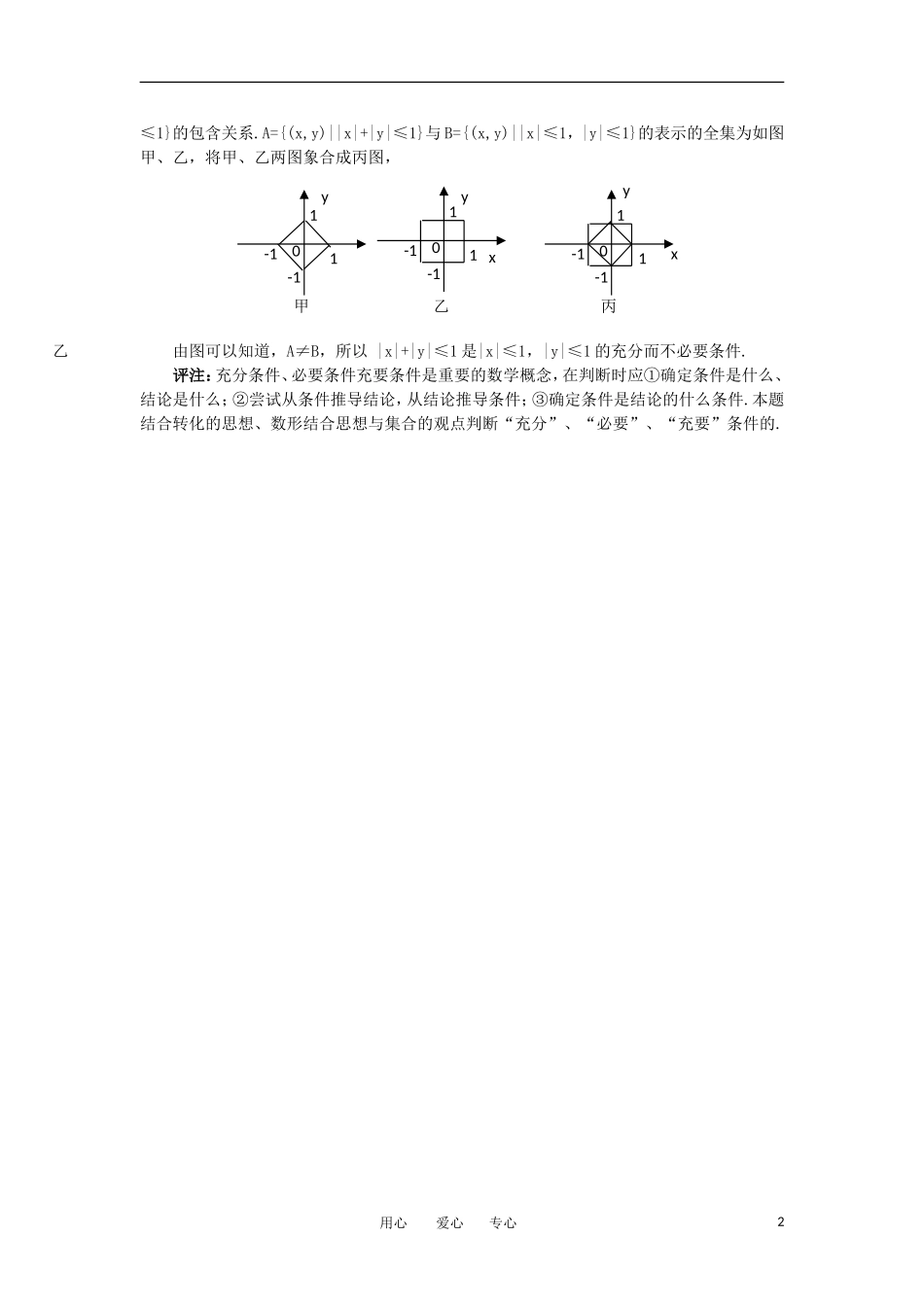
集合对简易逻辑注释数学是逻辑性很强的学科，基本逻辑知识是认识问题和研究问题不可缺少的工具，是我们进行学习、掌握和使用语言的基础，因此，学好逻辑的基础知识是非常必要的，而此内容对高中学生的难度是比较大的，为了帮助大家对此部分知识有深刻的理解和认识，下面用集合的观点来对某些逻辑知识进行解释.一、集合理论中的“交”、“并”、“补”运算渗透逻辑联结词“或”、“且”、“非”1、对“或”的理解可联想到集合中“并集”的概念，A∪B＝｛x|x∈A或x∈B｝中的元素“或”，它是指“x∈A”或“x∈B”中至少有一个是成立，即它所包含的三个方面：x∈A且x∈B；x∈A且x∈B；x∈A且x∈B中至少有一个是成立.2、对“且”的理解，可联想到集合中“交集”的概念，A∩B＝｛x|x∈A且x∈B｝中的“且”是指“x∈A”与“x∈B”这两个条件都要同时满足.3、对“非”的理解，可联想到集合中的“补集”概念，若命题中对应于集合P，则命题非P就应对应着集合P在全集U中的补集∁uP.例1写出若ab＜0则a＜0且b＞0的否命题分析：“若p则q”的否命题“若p则q”，它涉及了逻辑联结词的否定，对此我们从集合角度来看，a＜0且b＞0可表示为一个点集A，用图形表示(如图)，不满足“a＜0且b＞0”的点（a,b），在阴影的另一部分，即∁uA.它可以看作是Ｘ轴及以下部分(b≤0)和Ｙ轴及右侧部分（a≥0）部分合起来构成，即两块处域的并集，a、b满足“a≥0或b≤0”.因而，否命题为若a、b≥0则a≥0或b≤0.评注：“p且q”的否定为“非p或非q”，用集合的观点来解释，并结合图形，同学更容易接受并理解.例2把不等式＜0写成用“且”、“或”联结的整式的形式.分析：本题可结合不等式的解集进行解答：由于＜0，所以x﹣1与x﹣2异号，故不等式＜0的解集可以看成两个不等式x﹣1＞0与x﹣2＜0的解集的交集再与另两个不等式x﹣1＜0与x﹣2＞0交集的并集，即用“且”、“或”联结的整式的形式为：x﹣1＞0且x﹣2＜0或x﹣1＜0且x﹣2＞0.二、用集合理论中的“子集”来理解“充分条件”、“必要条件”、“充要条件”因为若pq，则p是q的充分条件；若pq，则p是q的必要条件.设P所对应的集合为A={x|p}，q所对应的集合为B={x|q}，则①若A(B，就是x∈A则x∈B，则A是B的充分条件，B是A的必要条件.②若A≠B，就是x∈A则x∈B，且A中至少有一个元素不在B中，则A是B的充分非必要条件，B是A的必要非充分条件.③若A=B，就是A(B且A(B，则A是B的充分条件，同时A是B的必要条件，即A是B的充要条件.④若AB，A/B，则A是B的既不充分也不必要条件.例3已知p是r的充分不必要条件，s是r的必要条件，q是s的必要条件．那么p是q成立的（）（A）充分不必要条件（B）必要不充分条件（C）充要条件（D）既不充分也不必要条件分析：设条件p、q、r、s相对应的集合为A、B、C、D，则根据题设条件知：A≠C，CD，DB，又由子集的传递性知A≠B，所以p是q成立充分不必要条件，故选A.例4对实数x、y、“|x|+|y|≤1”是“|x|≤1，|y|≤1”的什么条件?分析：从集合的角度判断，考虑集合A={(x,y)||x|+|y|≤1}与B={(x,y)||x|≤1，|y|用心爱心专心1ABＡyx０≤1}的包含关系.A={(x,y)||x|+|y|≤1}与B={(x,y)||x|≤1，|y|≤1}的表示的全集为如图甲、乙，将甲、乙两图象合成丙图，由图可以知道，A≠B，所以|x|+|y|≤1是|x|≤1，|y|≤1的充分而不必要条件.评注：充分条件、必要条件充要条件是重要的数学概念，在判断时应①确定条件是什么、结论是什么；②尝试从条件推导结论，从结论推导条件；③确定条件是结论的什么条件.本题结合转化的思想、数形结合思想与集合的观点判断“充分”、“必要”、“充要”条件的.用心爱心专心2-11-110y甲乙-11-110xy丙-11-110xy乙