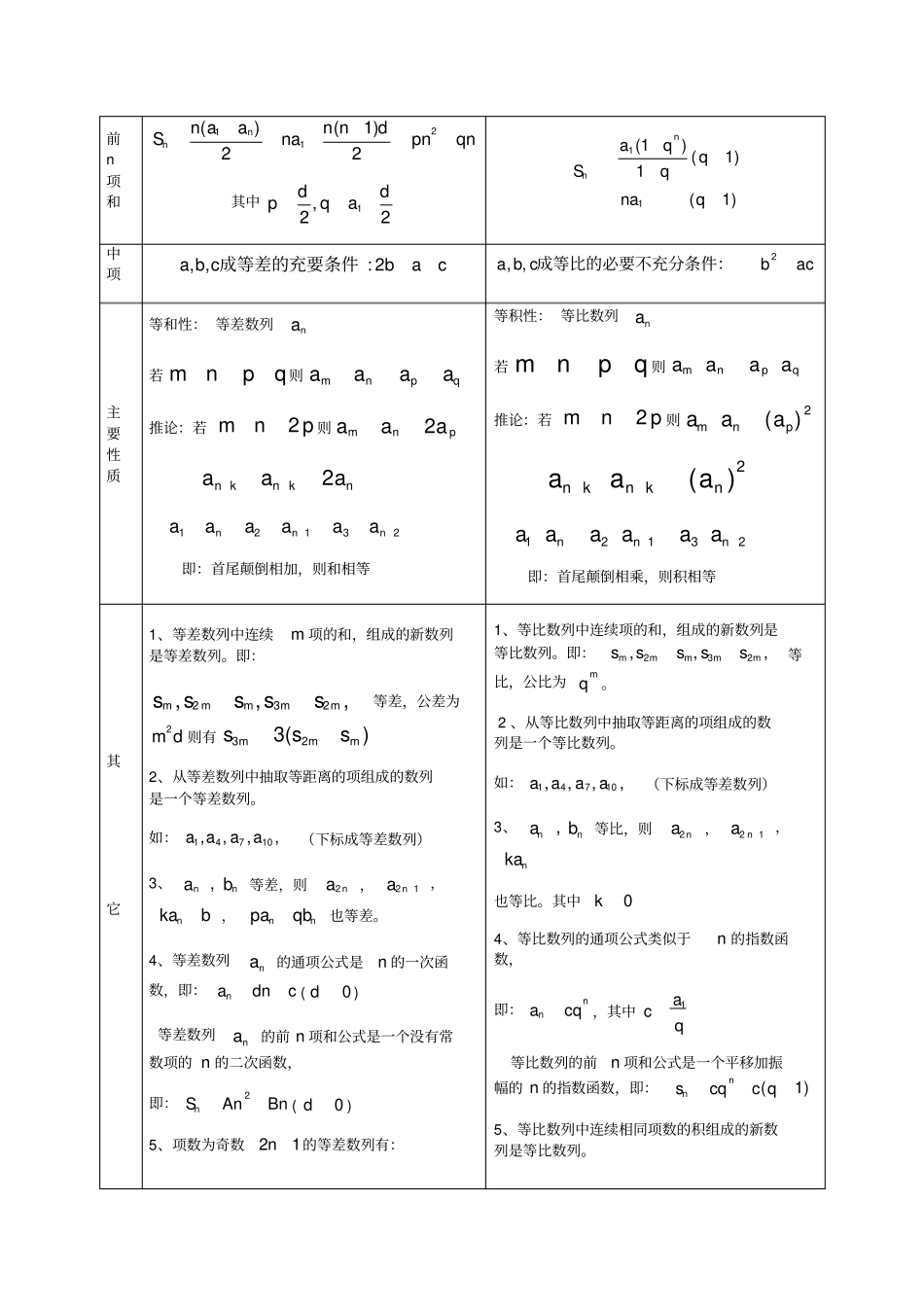
数列解题方法一、基础知识:数列:1.数列、项的概念:按一定次序排列的一列数,叫做数列,其中的每一个数叫做数列的项.2.数列的项的性质:①有序性;②确定性;③可重复性.3.数列的表示:通常用字母加右下角标表示数列的项,其中右下角标表示项的位置序号,因此数列的一般形式可以写成a1,a2,a3,⋯,an,(⋯),简记作{an}.其中an是该数列的第n项,列表法、图象法、符号法、列举法、解析法、公式法(通项公式、递推公式、求和公式)都是表示数列的方法.4.数列的一般性质:①单调性;②周期性.5.数列的分类:①按项的数量分:有穷数列、无穷数列;②按相邻项的大小关系分:递增数列、递减数列、常数列、摆动数列、其他;③按项的变化规律分:等差数列、等比数列、其他;④按项的变化围分:有界数列、无界数列.6.数列的通项公式:如果数列{an}的第n项an与它的序号n之间的函数关系可以用一个公式an=f(n)(n∈N+或其有限子集{1,2,3,⋯,n})来表示,那么这个公式叫做这个数列的通项公式.数列的项是指数列中一个确定的数,是函数值,而序号是指数列中项的位置,是自变量的值.由通项公式可知数列的图象是散点图,点的横坐标是项的序号值,纵坐标是各项的值.不是所有的数列都有通项公式,数列的通项公式在形式上未必唯一.7.数列的递推公式:如果已知数列{an}的第一项(或前几项),且任一项an与它的前一项an-1(或前几项an-1,an-2,⋯)间关系可以用一个公式an=f(a1n)(n=2,3,⋯)(或an=f(a1n,a2n)(n=3,4,5,⋯),⋯)来表示,那么这个公式叫做这个数列的递推公式.8.数列的求和公式:设Sn表示数列{an}和前n项和,即Sn=1niia=a1+a2+⋯+an,如果Sn与项数n之间的函数关系可以用一个公式Sn=f(n)(n=1,2,3,⋯)来表示,那么这个公式叫做这个数列的求和公式.9.通项公式与求和公式的关系:通项公式an与求和公式Sn的关系可表示为:11(1)(n2)nnnSnaSS等差数列与等比数列:等差数列等比数列文字定义一般地,如果一个数列从第二项起,每一项与它的前一项的差是同一个常数,那么这个数列就叫等差数列,这个常数叫等差数列的公差。一般地,如果一个数列从第二项起,每一项与它的前一项的比是同一个常数,那么这个数列就叫等比数列,这个常数叫等比数列的公比。符号定义1nnaad1(0)nnaqqa分类递增数列:0d递减数列:0d常数数列:0d递增数列:1101001aqaq,或,递减数列:1101001aqaq,或,摆动数列:0q常数数列:1q通项1(1)()nmaandpnqanmd其中1,pdqad11nnmnmaaqaq(0q)前n项和211()(1)22nnnaanndSnapnqn其中1,22ddpqa11(1)(1)1(1)nnaqqSqnaq中项,,2abcbac成等差的充要条件:2,,abcbac成等比的必要不充分条件:主要性质等和性:等差数列na若mnpq则mnpqaaaa推论:若2mnp则2mnpaaa2nknknaaa12132nnnaaaaaa即:首尾颠倒相加,则和相等等积性:等比数列na若mnpq则mnpqaaaa推论:若2mnp则2()mnpaaa2()nknknaaa12132nnnaaaaaa即:首尾颠倒相乘,则积相等其它1、等差数列中连续m项的和,组成的新数列是等差数列。即:232,,,mmmmmsssss等差,公差为2md则有323()mmmsss2、从等差数列中抽取等距离的项组成的数列是一个等差数列。如:14710,,,,aaaa(下标成等差数列)3、,nnab等差,则2na,21na,nkab,nnpaqb也等差。4、等差数列na的通项公式是n的一次函数,即:nadnc(0d)等差数列na的前n项和公式是一个没有常数项的n的二次函数,即:2nSAnBn(0d)5、项数为奇数21n的等差数列有:1、等比数列中连续项的和,组成的新数列是等比数列。即:232,,,mmmmmsssss等比,公比为mq。2、从等比数列中抽取等距离的项组成的数列是一个等比数列。如:14710,,,,aaaa(下标成等差数列)3、,nnab等比,则2na,21na,nka也等比。其中0k4、等比数列的通项公式类似于n的指数函数,即:nnacq,其中1acq等比数列的前n项和公式是一个平移加振幅的n的指数函数,即:(1)nnscqcq5、等比数列中连续相同项数的积组成的新数列是等比数列。性质1snsn奇偶nssaa奇偶中21(21)nnsna项数为偶数2n的等差数列有:1nnsasa奇偶,ssnd偶奇21()nnnsnaa6、,nmaman则0mnanmss则0()mnsnm,nmsmsn则()mnsmn证明方法证明...