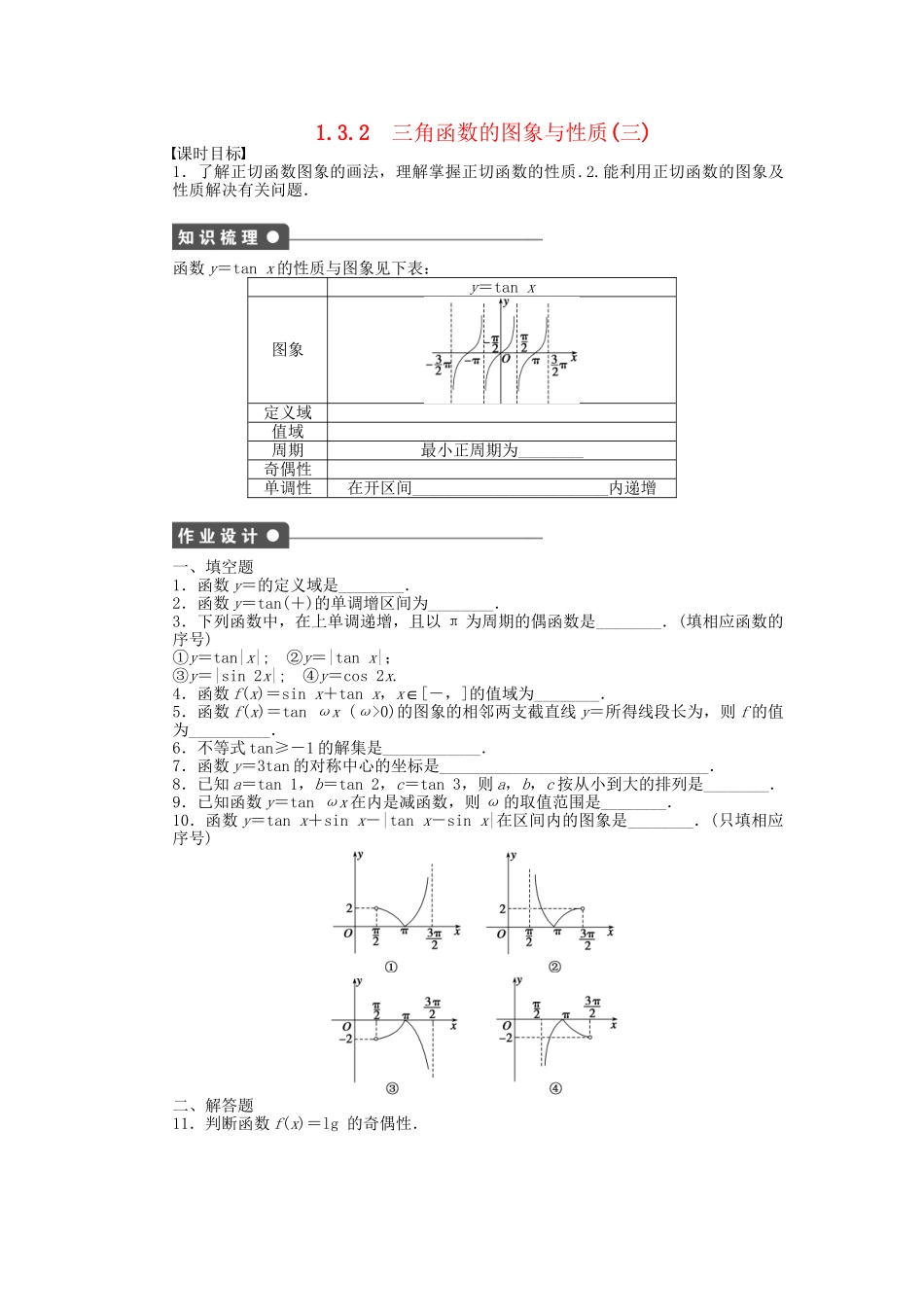
1.3.2三角函数的图象与性质(三)课时目标1.了解正切函数图象的画法,理解掌握正切函数的性质.2.能利用正切函数的图象及性质解决有关问题.函数y=tanx的性质与图象见下表:y=tanx图象定义域值域周期最小正周期为________奇偶性单调性在开区间________________________内递增一、填空题1.函数y=的定义域是________.2.函数y=tan(+)的单调增区间为________.3.下列函数中,在上单调递增,且以π为周期的偶函数是________.(填相应函数的序号)①y=tan|x|;②y=|tanx|;③y=|sin2x|;④y=cos2x.4.函数f(x)=sinx+tanx,x∈[-,]的值域为________.5.函数f(x)=tanωx(ω>0)的图象的相邻两支截直线y=所得线段长为,则f的值为__________.6.不等式tan≥-1的解集是____________.7.函数y=3tan的对称中心的坐标是_________________________________.8.已知a=tan1,b=tan2,c=tan3,则a,b,c按从小到大的排列是________.9.已知函数y=tanωx在内是减函数,则ω的取值范围是________.10.函数y=tanx+sinx-|tanx-sinx|在区间内的图象是________.(只填相应序号)二、解答题11.判断函数f(x)=lg的奇偶性.12.作出函数y=tan|x|的图象,根据图象判断其周期性,并求出单调区间.能力提升13.已知函数y=tanx在区间(-π,π)上递增,求a的取值范围.14.作出函数y=(tanx+|tanx|)的图象,并写出单调增区间.1.正切函数y=tanx在每段区间(k∈Z)上是单调递增函数,但不能说正切函数在其定义域内是单调递增函数.并且每个单调区间均为开区间,而不能写成闭区间(k∈Z).正切函数无单调减区间.2.正切函数是奇函数,图象关于原点对称,且有无穷多个对称中心,对称中心坐标是(,0)(k∈Z).正切函数的图象无对称轴,但图象以直线x=kπ+(k∈Z)为渐近线.1.3.2三角函数的图象与性质(三)知识梳理{x|x∈R,且x≠kπ+,k∈Z}Rπ奇函数(k∈Z)作业设计1.[kπ+,kπ+),k∈Z.2.(2kπ-,2kπ+)(k∈Z)解析由kπ-<+
sinx,y=2sinx.故填④.11.解由>0,得tanx>1或tanx<-1.∴函数定义域为∪(k∈Z)关于原点对称.f(-x)+f(x)=lg+lg=lg=lg1=0.∴f(-x)=-f(x),∴f(x)是奇函数.12.解y=tan|x|=根据y=tanx的图象,可作出y=tan|x|的图象(如图所示).由图可知,函数y=tan|x|不是周期函数,它是单调减区间为(-,0],(kπ-,kπ-),k=0,-1,-2…,;单调增区间为[0,),(kπ+,kπ+),k=0,1,2…,.13.解由π>-π,得a>0.故知(-π,π)⊆(-,),得故0