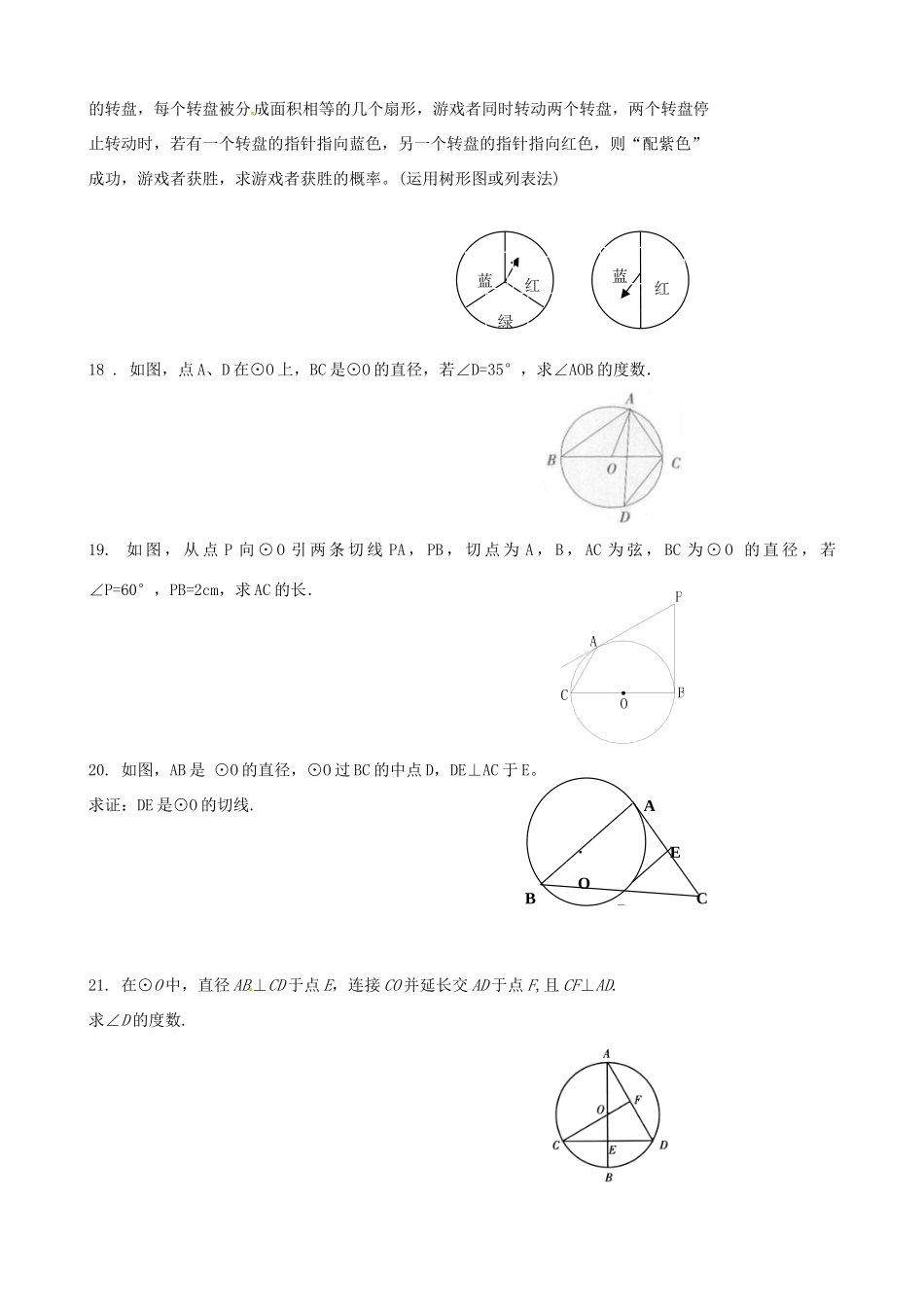
宁夏吴忠市红寺堡区第三中学2016届九年级数学上学期第三次专项测试试题一选择题(8x3分=24分)1.下列事件中,是必然事件的为()A.我市夏季的平均气温比冬季的平均气温高;B.每周的星期日一定是晴天;C.打开电视机,正在播放动画片;D.掷一枚均匀硬币,正面一定朝上.2.如图23-10,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=10,CD=8,那么AE的长为()A.2B.3C.4D.53.如图23-11,CA为⊙O的切线,切点为A,点B在⊙O上,如果∠CAB=55°,那么∠AOB等于()A.35°B.90°C.110°D.120°4.如图23-15,AB为⊙O的直径,弦CD⊥AB,垂足为E,那么下列结论不正确的是()A.CE=DEB.C.∠BAC=∠BADD.AC>AD5.如图4,一个小球从A点沿制定的轨道下落,在每个交叉口都有向左或向右两种机会均等的结果,小球最终到达H点的概率是()A.B.C.D.6.如图,四边形ABCD是⊙O的内接四边形,若∠BOD=88°,则∠BCD的度数是()A.88°B.92°C.106°D.136°7.如图23-22,⊙O、⊙B、⊙C、⊙D、⊙E相互外离,它们的半径都是1,顺次连结5个圆心得到五边形ABCDE,则图中五个扇形(阴影部分)的面积之和为()A.πB.1.5πC.2πD.2.5π8.⊙O的半径为10cm,弦AB∥CD,AB=12cm,CD=16cm,则AB和CD的距离为()A.2cmB.14cmC.2cm或14cmD.10cm或20cm二填空(8x3分=24分)9.某电视台综艺节目从接到的5000个热线电话中,抽取10名“幸运观众”,小颖打通了一次热线电话,她成为“幸运观众”的概率是.10.如图23-14,⊙O的直径为10,弦AB=8,P是弦AB上一个动点,那么OP的长的取值范围是_________.11.圆内接四边形ABCD中,∠A︰∠C=1︰3,则∠C=_________.12.在直径为52cm的圆柱形油桶内装入一些油后,截面如图23-16所示,如果油的最大深度为16cm,那么油面宽度为_________cm.13.已知圆锥的底面直径为4,母线长为6,则它的侧面积为_________.14.如图23-19,在△ABC中,∠C=90°,AC=3,BC=4,若以C为圆心,R为半径的圆与斜边AB只有一个公共点,则R的值是________.15.如图23-20,C是⊙O的直径AB延长线上一点,过C作⊙O的切线CD,D为切点,连结AD、OD、BD.请根据图中所给出的已知条件(不再标注或使用其他字母,不再添加任何辅助线),写出一个你认为正确的结论_________________.16.一个扇形的弧长为20πcm,面积为240πcm2,则该扇形的圆心角为__________.三、解答题(17题6分,18~19每题8分,20~24每题10分,共72分)17.小颖为九年级1班毕业联欢会设计了一个“配紫色”的游戏:如图是两个可以自由转动BCAPO的转盘,每个转盘被分成面积相等的几个扇形,游戏者同时转动两个转盘,两个转盘停止转动时,若有一个转盘的指针指向蓝色,另一个转盘的指针指向红色,则“配紫色”成功,游戏者获胜,求游戏者获胜的概率。(运用树形图或列表法)18.如图,点A、D在⊙O上,BC是⊙O的直径,若∠D=35°,求∠AOB的度数.19.如图,从点P向⊙O引两条切线PA,PB,切点为A,B,AC为弦,BC为⊙O的直径,若∠P=60°,PB=2cm,求AC的长.20.如图,AB是⊙O的直径,⊙O过BC的中点D,DE⊥AC于E。求证:DE是⊙O的切线.21.在⊙O中,直径AB⊥CD于点E,连接CO并延长交AD于点F,且CF⊥AD.求∠D的度数.绿蓝蓝红红DCEB·OA22.如图,AB是⊙O的直径,BC是弦,OD⊥BC于E,交弧BC于D.(1)请写出两个不同类型的正确结论;(2)若BC=8,ED=2,求⊙O的半径.23.有一个均匀的正六面体,六个面上分别标有数字1,2,3,4,5,6,随机地抛掷一次,把朝上一面的数字记为x;另有三张背面完全相同,正面分布写有数字﹣2,﹣1,1的卡片,将其混合后,正面朝下放置在桌面上,并从中随机地抽取一张,把卡片正面上的数字记为y;然后计算出S=x+y的值.(1)用树状图或列表法表示出S的所有可能情况;(2)求出当S<2时的概率.24.已知:如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点P,PD⊥AC于点D.(1)求证:PD是⊙O的切线;(2)若∠CAB=120°,AB=2,求BC的值.