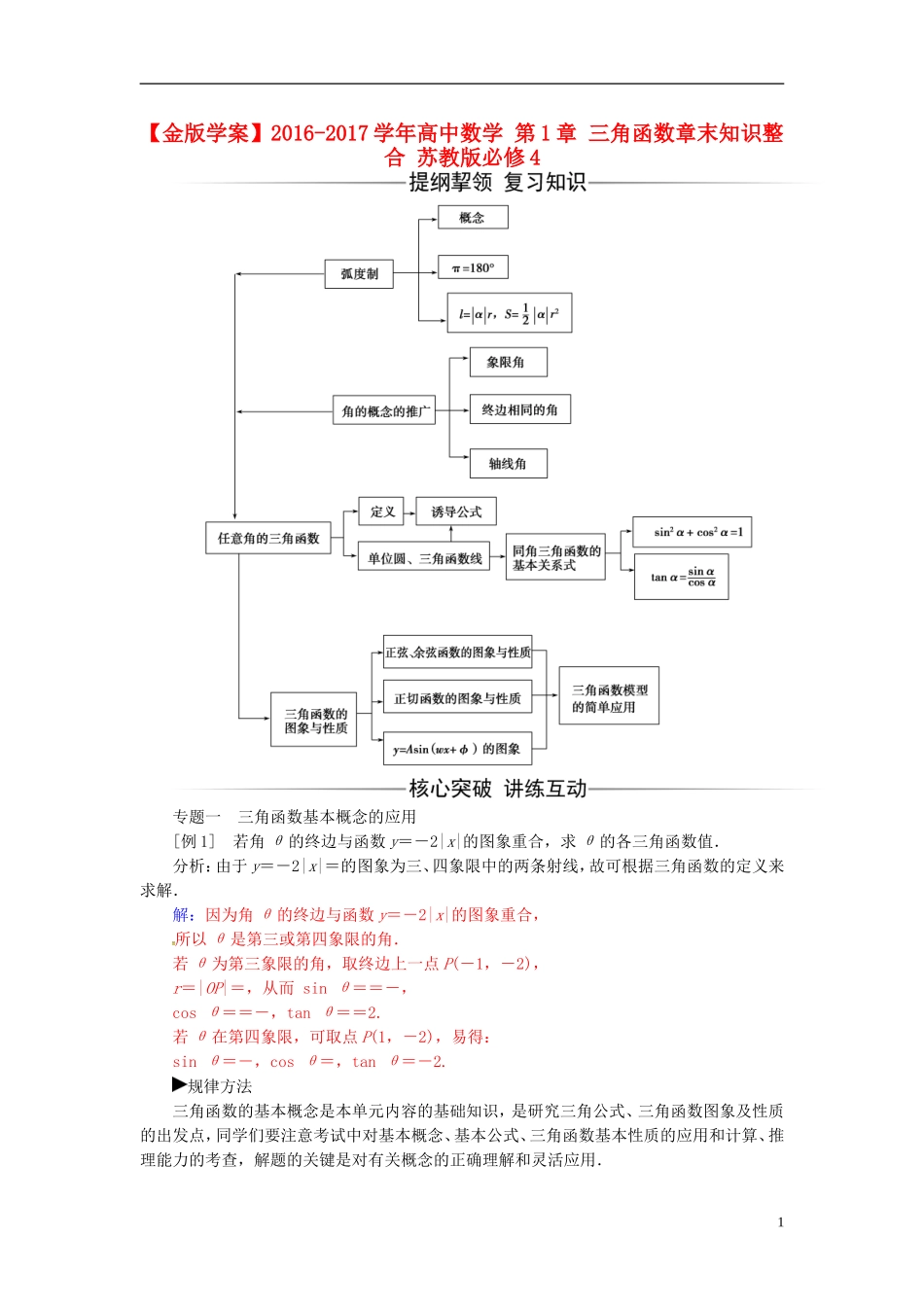
【金版学案】2016-2017学年高中数学第1章三角函数章末知识整合苏教版必修4专题一三角函数基本概念的应用[例1]若角θ的终边与函数y=-2|x|的图象重合,求θ的各三角函数值.分析:由于y=-2|x|=的图象为三、四象限中的两条射线,故可根据三角函数的定义来求解.解:因为角θ的终边与函数y=-2|x|的图象重合,所以θ是第三或第四象限的角.若θ为第三象限的角,取终边上一点P(-1,-2),r=|OP|=,从而sinθ==-,cosθ==-,tanθ==2.若θ在第四象限,可取点P(1,-2),易得:sinθ=-,cosθ=,tanθ=-2.规律方法三角函数的基本概念是本单元内容的基础知识,是研究三角公式、三角函数图象及性质的出发点,同学们要注意考试中对基本概念、基本公式、三角函数基本性质的应用和计算、推理能力的考查,解题的关键是对有关概念的正确理解和灵活应用.1[变式训练]函数f(x)=若f(1)+f(a)=2,则a的所有可能值为()A.1B.-C.1,-D.1,解析:此题可运用代入排除法.因为f(1)+f(a)=2,f(1)=e0=1,所以f(a)=1,选项中提供的a的可能值有三个,分别为1,,-,因此把这三个数代入f(x)中,值为1的即为所求.f(1)=e0=1,f=e-1,f=sin=1.所以a的所有可能值为1,-.答案:C专题二同角三角函数的基本关系与诱导公式[例2]已知=-4,求(sinθ-3cosθ)·(cosθ-sinθ)的值.解:法一:由已知=-4,所以2+tanθ=-4(1-tanθ),解得tanθ=2,所以(sinθ-3cosθ)(cosθ-sinθ)=4sinθcosθ-sin2θ-3cos2θ====.法二:由已知=-4,解得tanθ=2,即=2,所以sinθ=2cosθ.所以(sinθ-3cosθ)(cosθ-sinθ)=(2cosθ-3cosθ)·(cosθ-2cosθ)=cos2θ===.规律方法1.三角函数式的化简.求值与证明问题的依据主要是同角三角函数的关系式及诱导公式.2.解题中的常用技巧:(1)弦切互化,减少或统一函数名称.(2)“1”的代换,如:1=sin2α+cos2α(常用于解决有关正弦、余弦齐次式的化简求值问题中),1=tan等.(3)若式子中有角,k∈Z,则先利用诱导公式化简.[变式训练](2015·福建卷)若sinα=-,且α为第四象限角,则tanα的值等于()A.B.-C.D.-解析:法一:因为α为第四象限的角,故cosα===,所以tanα===-.法二:因为α是第四象限角,且sinα=-,所以可在α的终边上取一点P(12,-5),则tanα==-.答案:D专题三三角函数的图象及其变换[例3]已知函数f(x)=Asin(ωx+φ)的图象在y轴上的截距为1,它在y轴右侧的第一个最大值点和最小值点分别为(x0,2)和(x0+3π,-2).(1)求f(x)的解析式;2(2)将f(x)的图象上的所有点的横坐标缩短到原来的(纵坐标不变),然后再将所得的图象向x轴正方向平移个单位长度,得到函数g(x)的图象,写出函数g(x)的解析式,并用五点作图的方法画出g(x)在长度为一个周期的闭区间上的图象.分析:由题目可以获取以下主要信息:①要求的函数的形式是f(x)=Asin(ωx+φ);②图象与y轴交点是(0,1).③相邻的一个最大值点和最小值点分别是(x0,2)和(x0+3π,-2),其中x0>0.解答本题可先由已知求出A,ω,φ,然后再根据图象变换得到函数y=g(x).解:(1)由f(x)=Asin(ωx+φ)在y轴上的截距为1,最大值为2,得A=2,1=2sinφ,所以sinφ=,φ=.又因为两相邻的最大值点和最小值点分别为(x0,2)和(x0+3π,-2).所以T=2[(x0+3π)-x0]=6π,所以ω==.所以函数的解析式为f(x)=2sin.(2)压缩后函数的解析式为y=2sin,再平移得g(x)=2sin=2sin.列表、作图如下:x-0π2πxg(x)020-20规律方法三角函数图象是本章的重点内容,它是研究三角函数性质的根据,重点抓住图象的特征及变换与函数解析式中各变量之间的内在联系.主要考查两个方面的问题:一是根据图象写函数解析式,关键要把握图象与函数性质的关系,从而确定出相关的数值.对于y=Asin(ωx+φ)+b(A>0,ω>0)的解析式求解问题:ymax=M,ymin=m,则A=,b=;由T=求得ω的值;φ的值采取代入特殊点(顶点或平衡点)坐标法求得.二是关于三角函数图象的平移和伸缩,此类问题关键要搞清在x轴方向的左右平移或伸缩是对解析中的字母x的变...