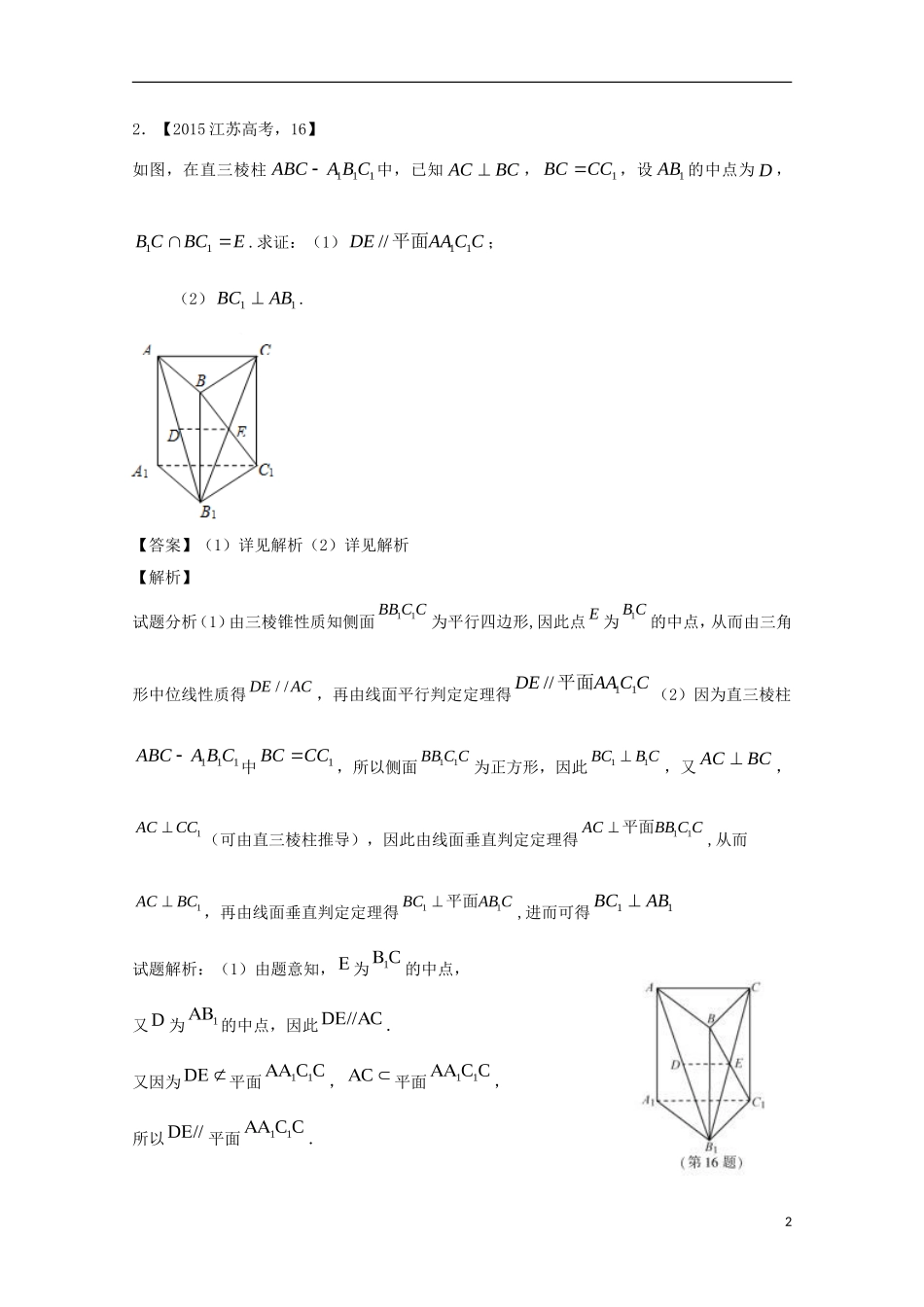
专题2点、直线、平面平行与垂直的判定与性质【三年高考】1.【2017江苏高考,15】如图,在三棱锥A-BCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E,F(E与A,D不重合)分别在棱AD,BD上,且EF⊥AD.求证:(1)EF∥平面ABC;(2)AD⊥AC.【答案】(1)见解析;(2)见解析.【解析】试题分析:(1)先由平面几何知识证明EFAB∥,再由线面平行判定定理得结论;(2)先由面面垂直性质定理得BC平面ABD,则BCAD,再由AB⊥AD及线面垂直判定定理得AD⊥平面ABC,即可得AD⊥AC.试题解析:(1)在平面ABD内,因为AB⊥AD,EFAD,所以EFAB∥.又因为EF平面ABC,AB平面ABC,所以EF∥平面ABC.【考点】线面平行判定定理、线面垂直判定与性质定理、面面垂直性质定理【名师点睛】垂直、平行关系证明中应用转化与化归思想的常见类型:(1)证明线面、面面平行,需转化为证明线线平行;(2)证明线面垂直,需转化为证明线线垂直;(3)证明线线垂直,需转化为证明线面垂直.12.【2015江苏高考,16】如图,在直三棱柱111CBAABC中,已知BCAC,1CCBC,设1AB的中点为D,EBCCB11.求证:(1)CCAADE11//平面;(2)11ABBC.【答案】(1)详见解析(2)详见解析【解析】试题分析(1)由三棱锥性质知侧面11BBCC为平行四边形,因此点E为1BC的中点,从而由三角形中位线性质得//DEAC,再由线面平行判定定理得CCAADE11//平面(2)因为直三棱柱111CBAABC中1CCBC,所以侧面11BBCC为正方形,因此11BCBC,又BCAC,1ACCC(可由直三棱柱推导),因此由线面垂直判定定理得11ACBBCC平面,从而1ACBC,再由线面垂直判定定理得11BCABC平面,进而可得11ABBC试题解析:(1)由题意知,为1C的中点,又D为1的中点,因此D//C.又因为D平面11CC,C平面11CC,所以D//平面11CC.2(2)因为棱柱111CC是直三棱柱,所以1CC平面C.因为C平面C,所以1CCC.又因为CC,1CC平面11CC,C平面11CC,1CCCC,所以C平面11CC.又因为1C平面11CC,所以1CC.因为1CCC,所以矩形11CC是正方形,因此11CC.因为C,1C平面1C,1CCC,所以1C平面1C.又因为1平面1C,所以11C.【考点定位】线面平行判定定理,线面垂直判定定理3.【2013江苏,理16】)如图,在三棱锥S-ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB.过A作AF⊥SB,垂足为F,点E,G分别是棱SA,SC的中点.求证:(1)平面EFG∥平面ABC;(2)BC⊥SA.【答案】(1)详见解析;(2)详见解析34.【2014江苏,理16】如图在三棱锥-PABC中,,,DEF分别为棱,,PCACAB的中点,已知,6,8,5PAACPABCDF,求证(1)直线//PA平面DEF;(2)平面BDE平面ABC.B【答案】证明见解析.【解析】试题分析:(1)本题证明线面平行,根据其判定定理,需要在平面DEF内找到一条与PA平行的直线,由于题中中点较多,容易看出//PADE,然后要交待PA在平面DEF外,DE在平面DEF内,即可证得结论;(2)要证两平面垂直,一般要证明一个平面内有一条直线与另一个平面垂直,由(1)可得DEAC,因此考虑能否证明DE与平面ABC内的另一条与AC相交的4直线垂直,由已知三条线段的长度,可用勾股定理证明DEEF,因此要找的两条相交直线就是,ACEF,由此可得线面垂直.试题解析:(1)由于,DE分别是,PCAC的中点,则有//PADE,又PADEF平面,DEDEF平面,所以//PADEF平面.(2)由(1)//PADE,又PAAC,所以PEAC,又F是AB中点,所以132DEPA,142EFBC,又5DF,所以222DEEFDF,所以DEEF,,EFAC是平面ABC内两条相交直线,所以DEABC平面,又DE平面BDE,所以平面BDE平面ABC.5.【2017课标1,文6】如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直接AB与平面MNQ不平行的是A.B.C.D.【答案】A【解析】5【考点】空间位置关系判断【名师点睛】本题主要考查线面平行的判定定理以及空间想象能力,属容易题.证明线面平行的常用方法:①利用线面平行的判定...