九年级数学下册 72正弦、余弦教材深度解析(教材知识详析拉分典例探究知识整合能力提升评估，pdf) 新人教版试卷VIP免费

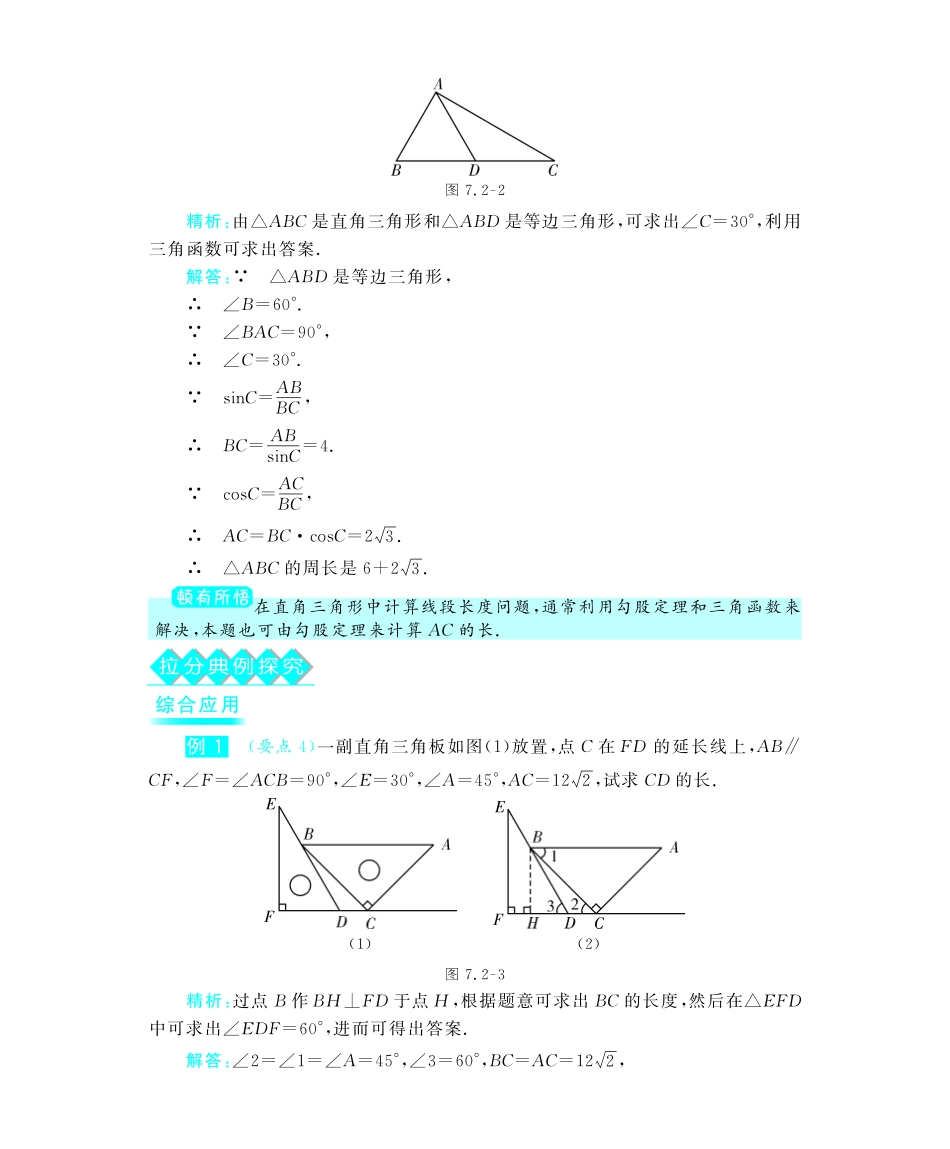
７．２正弦、余弦学习目标导航１．知道锐角的正弦、余弦的概念．２．会利用计算器求一个锐角的正弦、余弦．３．能说出锐角的正弦值随着锐角的增大而增大,余弦值随着锐角的增大而减少．教材知识详析要点１锐角正弦、余弦的概念(１)在△ABC中,∠C＝９０°,∠A、∠B、∠C的对边分别是a,b,c,锐角A的对边与斜边的比叫做∠A的正弦,记为sinA＝ac;锐角A的邻边与斜边的比叫做∠A的余弦,记为cosA＝bc．(２)对于锐角A的正弦和余弦来说,实质上就是直角三角形中两边之比,它的值只与角的度数有关．例１在△ABC中,∠C＝９０°,sinA＝４５,则tanB的值为()．A．４３B．３４C．３５D．４５精析:sinA＝４５,设BC＝４k,AB＝５k,根据勾股定理得AC＝３k．∴tanB＝ACBC＝３k４k＝３４．解答:B．解答这类习题可通过画图解题,可降低求解的难度．要点２三角函数的概念锐角A的正弦、余弦和正切都是∠A的三角函数．在锐角三角函数中,∠A是自变量,其取值范围是０°＜∠A＜９０°,三个比值是因变量．当∠A确定时,三个比值分别唯一确定;当∠A变化时,三个比值也分别有唯一确定的值与之对应．例２在Rt△ABC中,∠C＝９０°,a＝３,c＝５,求sinA和tanA的值．精析:由本题条件可以知道三角形的另一边,再根据锐角三角函数的意义求得结果．解答:在Rt△ABC中,c＝５,a＝３,∴b＝c２－a２＝５２－３２＝４．∴sinA＝ac＝３５,tanA＝ab＝３４．要点３等角、互余角的正弦、余弦之间的关系在△ABC中,∠C＝９０°,sinA＝cosB,sinB＝cosA．(１)sin(９０°－A)＝cosA;(２)cos(９０°－A)＝sinA;(３)sin２A＋cos２A＝１．例３如图７．２Ｇ１,在Rt△ABC中,BC、AC、AB三边的长分别为a,b,c,则sinA＝ac,cosA＝bc,tanA＝ab．我们不难发现:sin２６０°＋cos２６０°＝１,􀆺,试探求sinA、cosA、tanA之间存在的一般关系,并说明理由．图７．２Ｇ１精析:由三角函数的意义结合勾股定理不难解答．解答:存在的一般关系有:(１)sin２A＋cos２A＝１;(２)tanA＝sinAcosA．(１) sinA＝ac,cosA＝bc,a２＋b２＝c２,∴sin２A＋cos２A＝a２c２＋b２c２＝a２＋b２c２＝c２c２＝１．(２) sinA＝ac,cosA＝bc,∴tanA＝ab＝acbc＝sinAcosA．同一直角三角形中两个锐角互余,在此条件下,可由三角函数的定义,找到存在的等量关系．要点４能用三角函数的知识根据三角形中已知的边和角求出未知的边和角例４如图,已知在Rt△ABC中,∠BAC＝９０°,点D在边BC上,且△ABD是等边三角形．若AB＝２,求△ABC的周长．(结果保留根号)图７．２Ｇ２精析:由△ABC是直角三角形和△ABD是等边三角形,可求出∠C＝３０°,利用三角函数可求出答案．解答: △ABD是等边三角形,∴∠B＝６０°． ∠BAC＝９０°,∴∠C＝３０°． sinC＝ABBC,∴BC＝ABsinC＝４． cosC＝ACBC,∴AC＝BC􀅰cosC＝２３．∴△ABC的周长是６＋２３．在直角三角形中计算线段长度问题,通常利用勾股定理和三角函数来解决,本题也可由勾股定理来计算AC的长．拉分典例探究综合应用例１(要点４)一副直角三角板如图(１)放置,点C在FD的延长线上,AB∥CF,∠F＝∠ACB＝９０°,∠E＝３０°,∠A＝４５°,AC＝１２２,试求CD的长．(１)(２)图７．２Ｇ３精析:过点B作BH⊥FD于点H,根据题意可求出BC的长度,然后在△EFD中可求出∠EDF＝６０°,进而可得出答案．解答:∠２＝∠１＝∠A＝４５°,∠３＝６０°,BC＝AC＝１２２,作BH⊥FC于点H,则BH＝CH＝２２BC＝１２,在Rt△BDH中,DH＝BH÷tan∠３＝１２÷３＝４３,∴CD＝CH－DH＝１２－４３．归纳􀅰演绎:解答此类题目的关键根据题意建立三角形,利用所学的三角函数的关系进行解答．例２(要点４)通过学习三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化．类似的,可以在等腰三角形中建立边角之间的联系．我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad)．如图７．２Ｇ４(１),在△ABC中,AB＝AC,顶角A的正对记作sadA,这时sadA＝底边腰＝BCAB．容易知道一个角的大小与这个角的正对值也是相互唯一确定的．根据上述角的正对定义,解下列问题:(１)sad６０°＝;(２)对于０°＜A＜１８０°,∠A的正对值sadA的取值范围是;(３)如图７．...