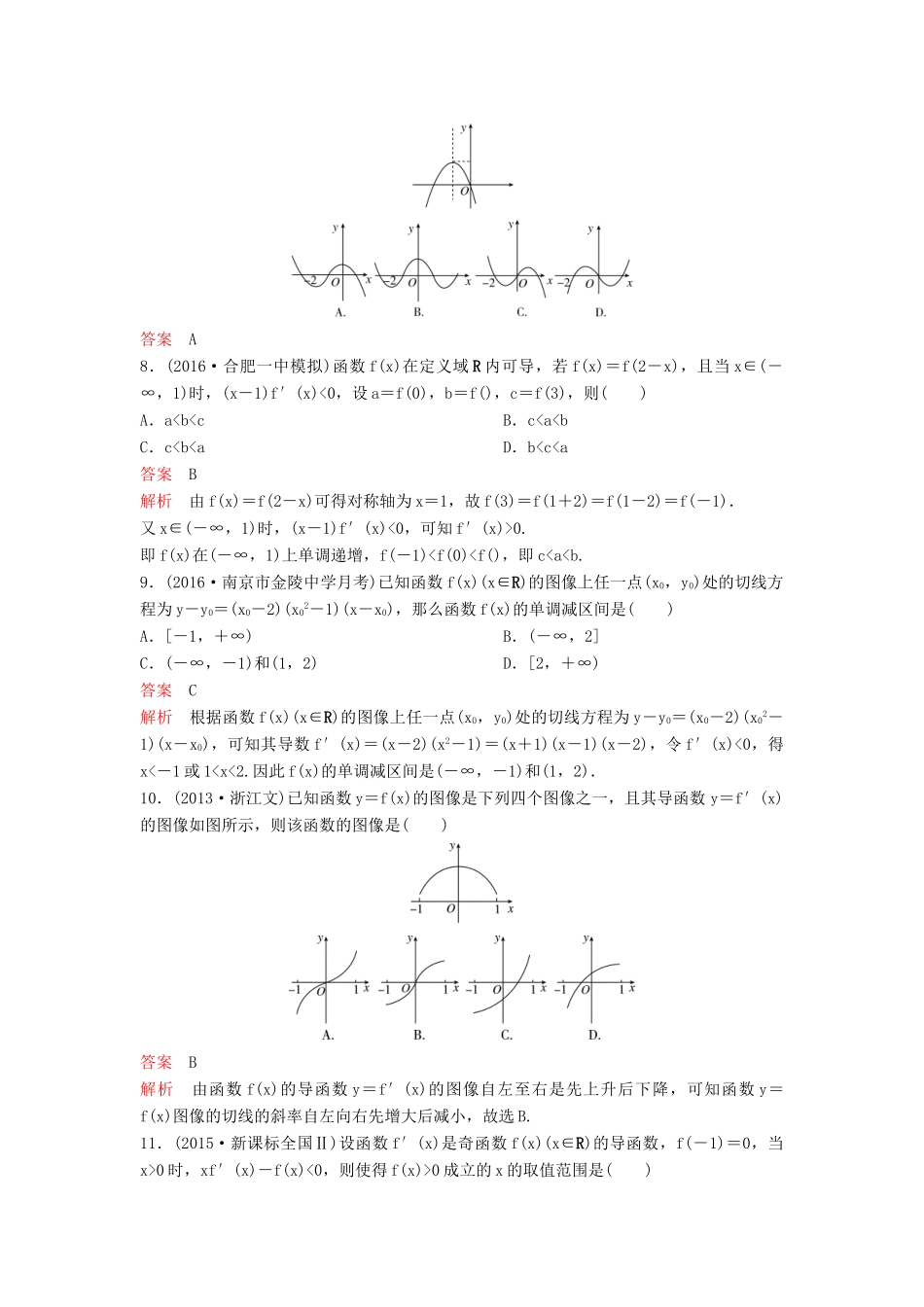
题组层级快练(十五)1.当x>0时,f(x)=x+的单调减区间是()A.(2,+∞)B.(0,2)C.(,+∞)D.(0,)答案B解析f′(x)=1-=<0,又 x>0,∴x∈(0,2),∴选B.2.函数f(x)=1+x-sinx在(0,2π)上是()A.增函数B.减函数C.在(0,π)上增,在(π,2π)上减D.在(0,π)上减,在(π,2π)上增答案A解析 f′(x)=1-cosx>0,∴f(x)在(0,2π)上递增.3.已知e为自然对数的底数,则函数y=xex的单调递增区间是()A.[-1,+∞)B.(-∞,-1]C.[1,+∞)D.(-∞,1]答案A解析令y′=(1+x)ex≥0. ex>0,∴1+x≥0,∴x≥-1,选A.4.(2016·长沙雅礼中学模拟)已知函数f(x)=x3+ax+4,则“a>0”是“f(x)在R上单调递增”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件答案A解析f′(x)=x2+a,当a≥0时,f′(x)≥0恒成立,故“a>0”是“f(x)在R上单调递增”的充分不必要条件.5.若函数y=a(x3-x)的递减区间为(-,),则a的取值范围是()A.a>0B.-1<a<0C.a>1D.0<a<1答案A解析y′=a(3x2-1),解3x2-1<0,得-<x<.∴f(x)=x3-x在(-,)上为减函数.又y=a·(x3-x)的递减区间为(-,).∴a>0.6.函数f(x)=lnx-ax(a>0)的单调递增区间为()A.(0,)B.(,+∞)C.(-∞,)D.(-∞,a)答案A解析由f′(x)=-a>0,得0
0.即f(x)在(-∞,1)上单调递增,f(-1)0时,xf′(x)-f(x)<0,则使得f(x)>0成立的x的取值范围是()A.(-∞,-1)∪(0,1)B.(-1,0)∪(1,+∞)C.(-∞,-1)∪(-1,0)D.(0,1)∪(1,+∞)答案A解析令F(x)=,因为f(x)为奇函数,所以F(x)为偶函数,由于F′(x)=,当x>0时,xf′(x)-f(x)<0,所以F(x)=在(0,+∞)上单调递减,根据对称性,F(x)=在(-∞,0)上单调递增,又f(-1)=0,f(1)=0,数形结合可知,使得f(x)>0成立的x的取值范围是(-∞,-1)∪(0,1).故选A.12.若函数f(x)的导函数为f′(x)=x2-4x+3,则函数f(x+1)的单调递减区间是________.答案(0,2)13.(2016·保定模拟)已知函数f(x)的导函数为f′(x)=5+cosx,x∈(-1,1),且f(0)=0,若f(1-x)+f(1-x2)<0,则实数x的取值范围为________.答案(1,)解析 导函数是偶函数,∴原函数f(x)是奇函数,且定义域为(-1,1).又导函数值恒大于0,∴原函数在定义域上单调递增,∴所求不等式变形为f(1-x)1,则不等式f(x)-x>0的解集为________.答案(2,+∞)解析令g(x)=f(x)-x,∴g′(x)=f′(x)-1.由题意知g′(x)>0,∴g(x)为增函数. g(2)=f(2)-2=0,∴g(x)>0的解集为(2...