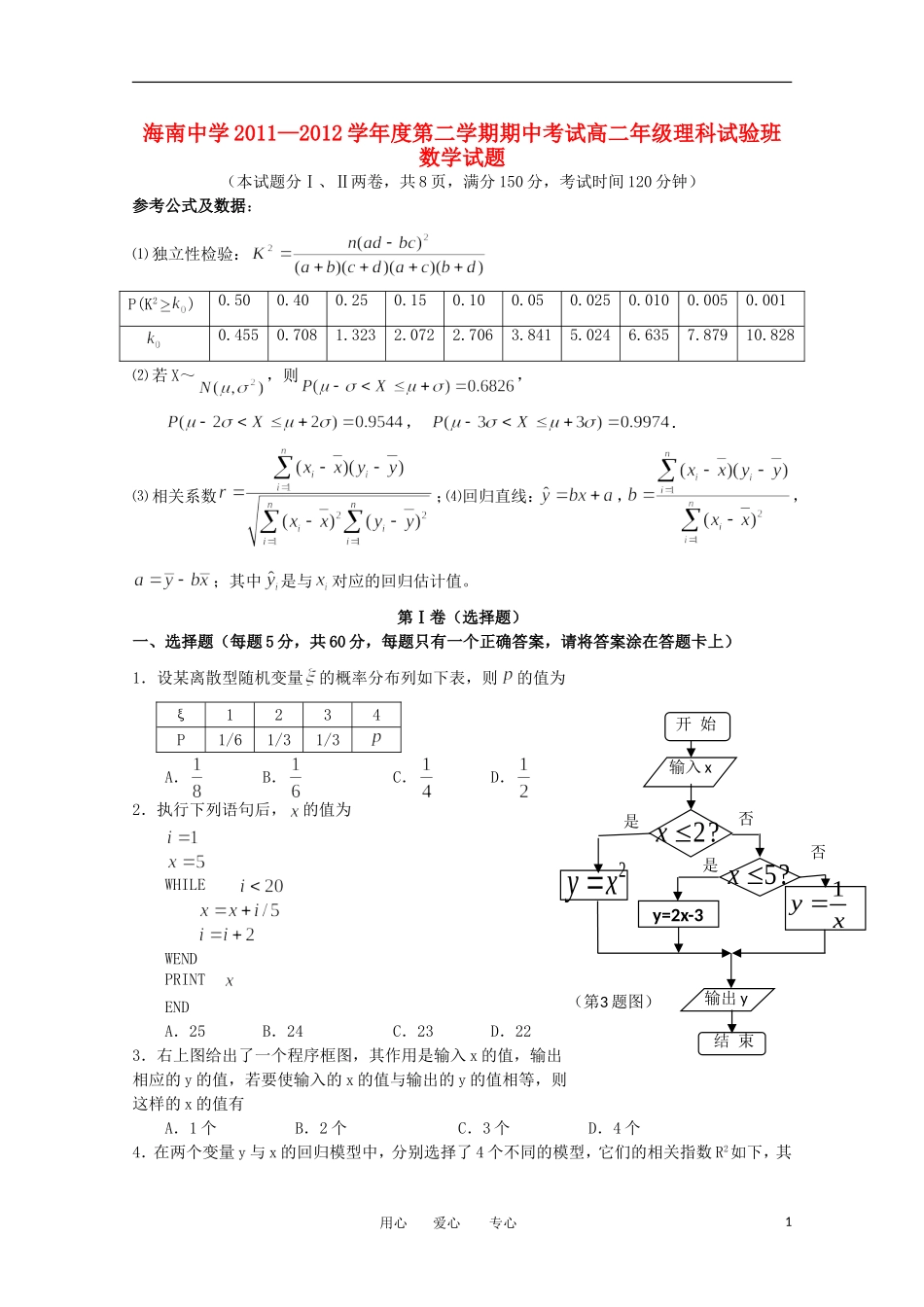
海南中学2011—2012学年度第二学期期中考试高二年级理科试验班数学试题(本试题分Ⅰ、Ⅱ两卷,共8页,满分150分,考试时间120分钟)参考公式及数据:⑴独立性检验:⑵若X~,则,,.⑶相关系数;⑷回归直线:,,;其中是与对应的回归估计值。第Ⅰ卷(选择题)一、选择题(每题5分,共60分,每题只有一个正确答案,请将答案涂在答题卡上)1.设某离散型随机变量的概率分布列如下表,则的值为ξ1234P1/61/31/3A.B.C.D.2.执行下列语句后,的值为WHILEWENDPRINTENDA.25B.24C.23D.223.右上图给出了一个程序框图,其作用是输入x的值,输出相应的y的值,若要使输入的x的值与输出的y的值相等,则这样的x的值有A.1个B.2个C.3个D.4个4.在两个变量y与x的回归模型中,分别选择了4个不同的模型,它们的相关指数R2如下,其用心爱心专心P(K2)0.500.400.250.150.100.050.0250.0100.0050.0010.4550.7081.3232.0722.7063.8415.0246.6357.87910.8281否开始输入x2?x5?x是是2yxy=2x-31yx输出y结束否(第3题图)7899446473中拟合效果最好的模型是A.模型4的相关指数R2为0.25B.模型2的相关指数R2为0.50C.模型3的相关指数R2为0.80D.模型1的相关指数R2为0.985.右图是2011年海南中学十大歌手年度总决赛中,七位评委为某位选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为A.84,4.84B.84,1.6C.85,1.6D.85,46.从装有2个红球和2个白球的口袋里任取2个球,那么互斥而不对立的两个事件是A.至少1个白球,都是白球B.至少1个白球,至少1个红球C.至少1个白球,都是红球D.恰好1个白球,恰好2个白球7.电子钟一天显示的时间是从00:00到23:59的每一时刻都由四个数字组成,则一天中任一时刻的四个数字之和为23的概率为A.B.C.D.8.同时转动如图所示的两个转盘,记转盘甲得到的数为x,转盘乙得到的数为y,构成数对(x,y),则所有数对(x,y)中满足xy=4的概率为A.B.C.D.9.若X是离散型随机变量,P(X=x1)=,P(X=x2)=,且x1