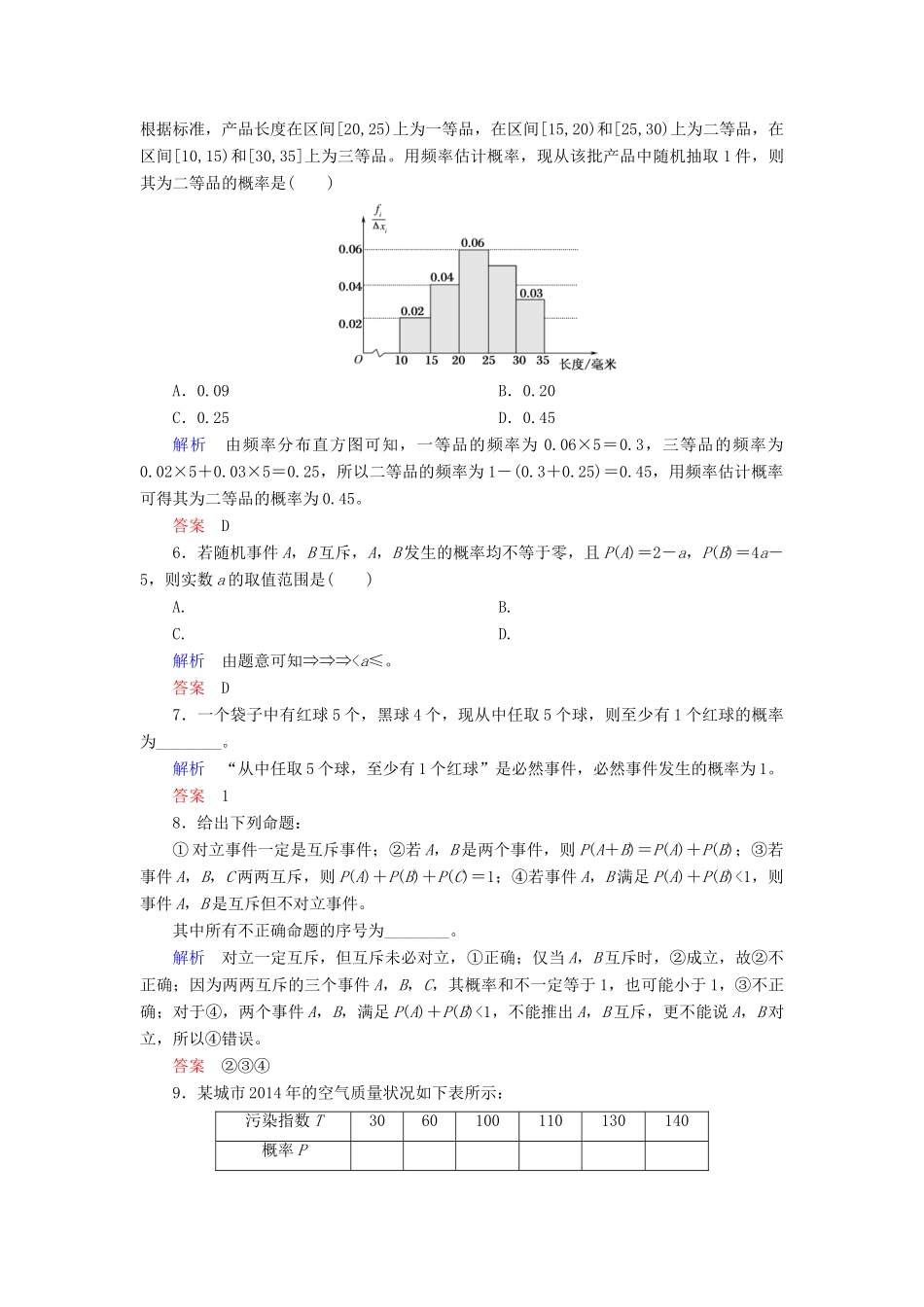
计时双基练五十五随机事件的概率A组基础必做1.(2016·九江模拟)从1,2,3,…,7这7个数中任取两个数,其中:(1)恰有一个是偶数和恰有一个是奇数;(2)至少有一个是奇数和两个都是奇数;(3)至少有一个是奇数和两个都是偶数;(4)至少有一个是奇数和至少有一个是偶数。上述事件中,是对立事件的是()A.(1)B.(2)(4)C.(3)D.(1)(3)解析(3)中“至少有一个是奇数”即“两个奇数或一奇一偶”,而从1~7中任取两个数根据取到数的奇偶性可认为共有三个事件:“两个都是奇数”与“一奇一偶”“两个都是偶数”,故“至少有一个是奇数”与“两个都是偶数”是对立事件。易知其余都不是对立事件。答案C2.(2015·湖北卷)我国古代数学名著《数书九章》有“米谷粒分”题:粮仓开仓收粮,有人送来米1534石,验得米内夹谷,抽样取米一把,数得254粒内夹谷28粒,则这批米内夹谷约为()A.134石B.169石C.338石D.1365石解析由条件知254粒内夹谷28粒,可估计米内夹谷的概率为=,所以1534石米中夹谷约为×1534≈169(石)。答案B3.在5张电话卡中,有3张移动卡和2张联通卡,从中任取2张,若事件“2张全是移动卡”的概率是,那么概率是的事件是()A.至多有一张移动卡B.恰有一张移动卡C.都不是移动卡D.至少有一张移动卡解析至多有一张移动卡包含“一张移动卡,一张联通卡”“两张全是联通卡”两个事件,它是“2张全是移动卡”的对立事件,故选A。答案A4.已知甲、乙两人下棋,和棋的概率为,乙胜的概率为,则甲胜的概率和甲不输的概率分别为()A.,B.,C.,D.,解析“甲胜”是“和棋或乙胜”的对立事件,所以“甲胜”的概率为1--=。设“甲不输”为事件A,则A可看做是“甲胜”与“和棋”这两个互斥事件的和事件,所以P(A)=+=。(或设“甲不输”为事件A,则A可看做是“乙胜”的对立事件,所以P(A)=1-=)答案C5.对一批产品的长度(单位:毫米)进行抽样检测,如图为检测结果的频率分布直方图。根据标准,产品长度在区间[20,25)上为一等品,在区间[15,20)和[25,30)上为二等品,在区间[10,15)和[30,35]上为三等品。用频率估计概率,现从该批产品中随机抽取1件,则其为二等品的概率是()A.0.09B.0.20C.0.25D.0.45解析由频率分布直方图可知,一等品的频率为0.06×5=0.3,三等品的频率为0.02×5+0.03×5=0.25,所以二等品的频率为1-(0.3+0.25)=0.45,用频率估计概率可得其为二等品的概率为0.45。答案D6.若随机事件A,B互斥,A,B发生的概率均不等于零,且P(A)=2-a,P(B)=4a-5,则实数a的取值范围是()A.B.C.D.解析由题意可知⇒⇒⇒