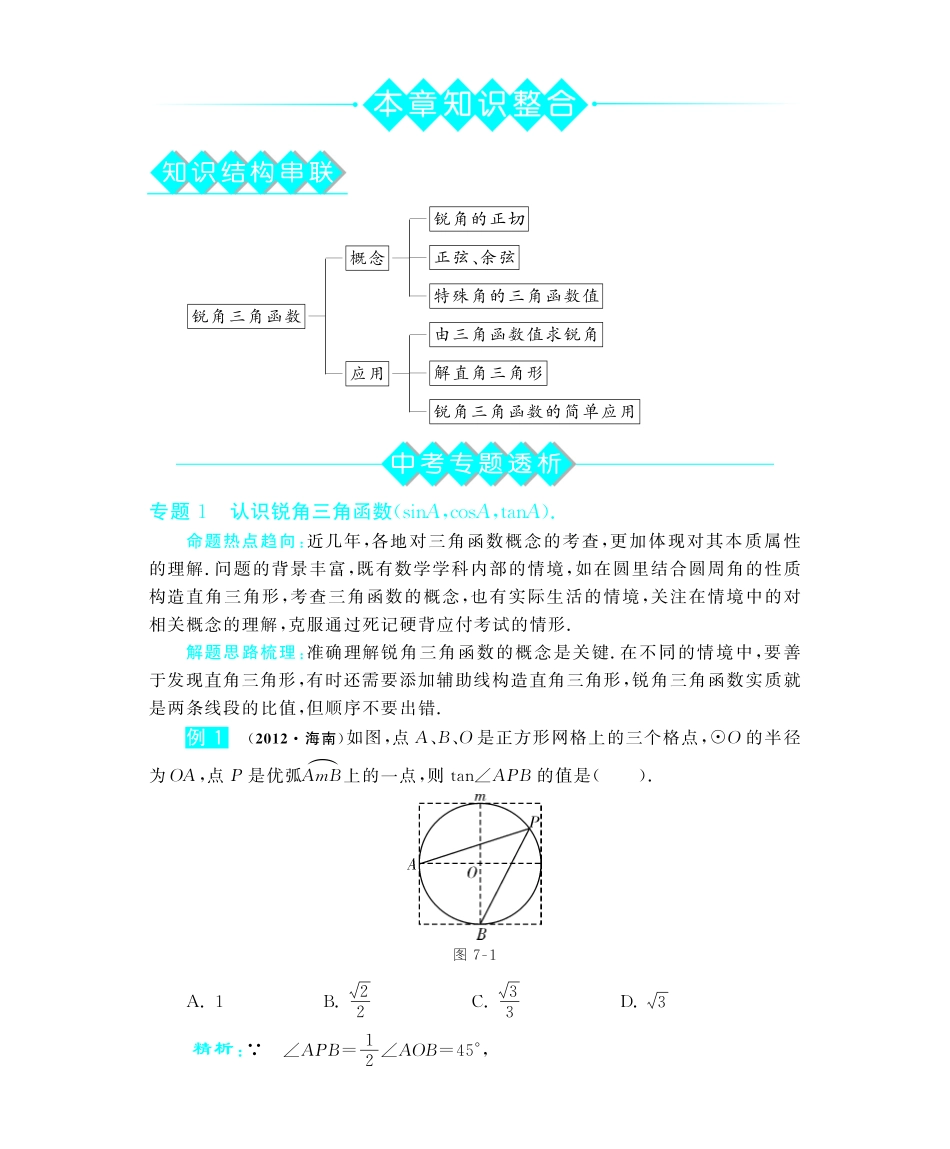
知识结构串联锐角三角函数——概念——锐角的正切—正弦、余弦—特殊角的三角函数值—应用——由三角函数值求锐角—解直角三角形—锐角三角函数的简单应用中考专题透析专题1认识锐角三角函数(sinA,cosA,tanA).命题热点趋向:近几年,各地对三角函数概念的考查,更加体现对其本质属性的理解.问题的背景丰富,既有数学学科内部的情境,如在圆里结合圆周角的性质构造直角三角形,考查三角函数的概念,也有实际生活的情境,关注在情境中的对相关概念的理解,克服通过死记硬背应付考试的情形.解题思路梳理:准确理解锐角三角函数的概念是关键.在不同的情境中,要善于发现直角三角形,有时还需要添加辅助线构造直角三角形,锐角三角函数实质就是两条线段的比值,但顺序不要出错.例1(2012海南)如图,点A、B、O是正方形网格上的三个格点,☉O的半径为OA,点P是优弧AmB︵上的一点,则tan∠APB的值是().图7G1A.1B.22C.33D.3精析: ∠APB=12∠AOB=45°,∴tan∠APB=tan45°=1.故选A.解答:A.专题2知道30°、45°、60°角的三角函数值.命题热点趋向:特殊角的三角函数值的考查也是中考常考内容,可以直接以填空题或选择题来考查,也可以含在实数运算中,也可以渗透在解决实际问题,以突出其应用价值.解题思路梳理:应熟记特殊角的三角函数值,具体问题中的特殊角,有的直接给出,有的则要经过分析判断而得,另外要能根据特殊角的三角函数值获知相关线段之间的数量关系.例2(2011山东烟台)如果在△ABC中,sinA=cosB=22,那么下列最确切的结论是().A.△ABC是直角三角形B.△ABC是等腰三角形C.△ABC是等腰直角三角形D.△ABC是锐角三角形精析:由sinA=cosB=22,得A=B=45°,从而C=90°,所以△ABC是等腰直角三角形,所以选C.解答:C.例3(2012四川德阳)某时刻海上点P处有一客轮,测得灯塔A位于客轮P的北偏东30°方向,且相距20海里.客轮以60海里/小时的速度沿北偏西60°方向航行23小时到达B处,那么tan∠ABP等于().A.12B.2C.55D.255精析:如图所示,根据题意可知∠APB=90°.且AP=20,PB=60×23=40.所以tan∠ABP=PAPB=2040=12,故选A.图7G2解答:A.例4(2012江苏泰州)如图,一居民楼底部B与山脚P位于同一水平线上,小李在P处测得居民楼顶A的仰角为60°,然后他从P处沿坡角为45°的山坡上走到C处,这时,PC=30m,点C与点A在同一水平线上,A、B、P、C在同一平面内.(1)求居民楼AB的高度;(2)求C、A两点之间的距离.(精确到0.1m,参考数据:2≈1.41,3≈1.73,6≈2.45)图7G3精析:过点C作BP的垂线,垂足为G,利用特殊Rt△PCG和Rt△ABP中的边角关系,我们容易计算出CG(即AB)的长,最后用AC=BP+PG,就是C、A两点之间的距离.解答:(1)过点C作BP的垂线,垂足为G,在Rt△PCG中,CG=PCsin45°=30×22=152,所以AB=152=21.2(m).(2)PG=PCcos45°=30×22=152,BP=1523=56,所以C、A两点之间的距离=BP+PG=152+56=33.5(m).点拨:解直角三角形是每年中考的必考知识点之一,主要考查直角三角形的边角关系及其应用,难度一般不会很大,本题是基本概念的综合题,主要考查考生应用知识解决问题的能力,很容易上手,容易出错的地方是近似值的取舍.专题3由已知锐角求它的三角函数值,由已知三角函数值求它对应的锐角.命题热点趋向:特殊角的三角函数值是中考的常考内容,考查的形式多样,有的直接以填空题或选择题来考查,有的含在解答题之中,但考查的要点就是:可以由特殊角知道其三角函数值,也可以由三角函数值知道特殊角的大小.解题思路梳理:熟记特殊角的三角函数值,从角与三角函数值的对应关系来理解,对15°、36°、75°等角的三角函数值的求解,则要利用三角函数的定义来研究.例5(1)(2012天津)2cos60°的值等于().A.1B.2C.3D.2精析:直接根据特殊角的三角函数值代入计算,cos60°=12,所以2cos60°=1.解答:A.(2)(2012山东济宁)在△ABC中,若∠A、∠B满足cosA-12+sinB-22æèçöø÷2=0,则∠C=...