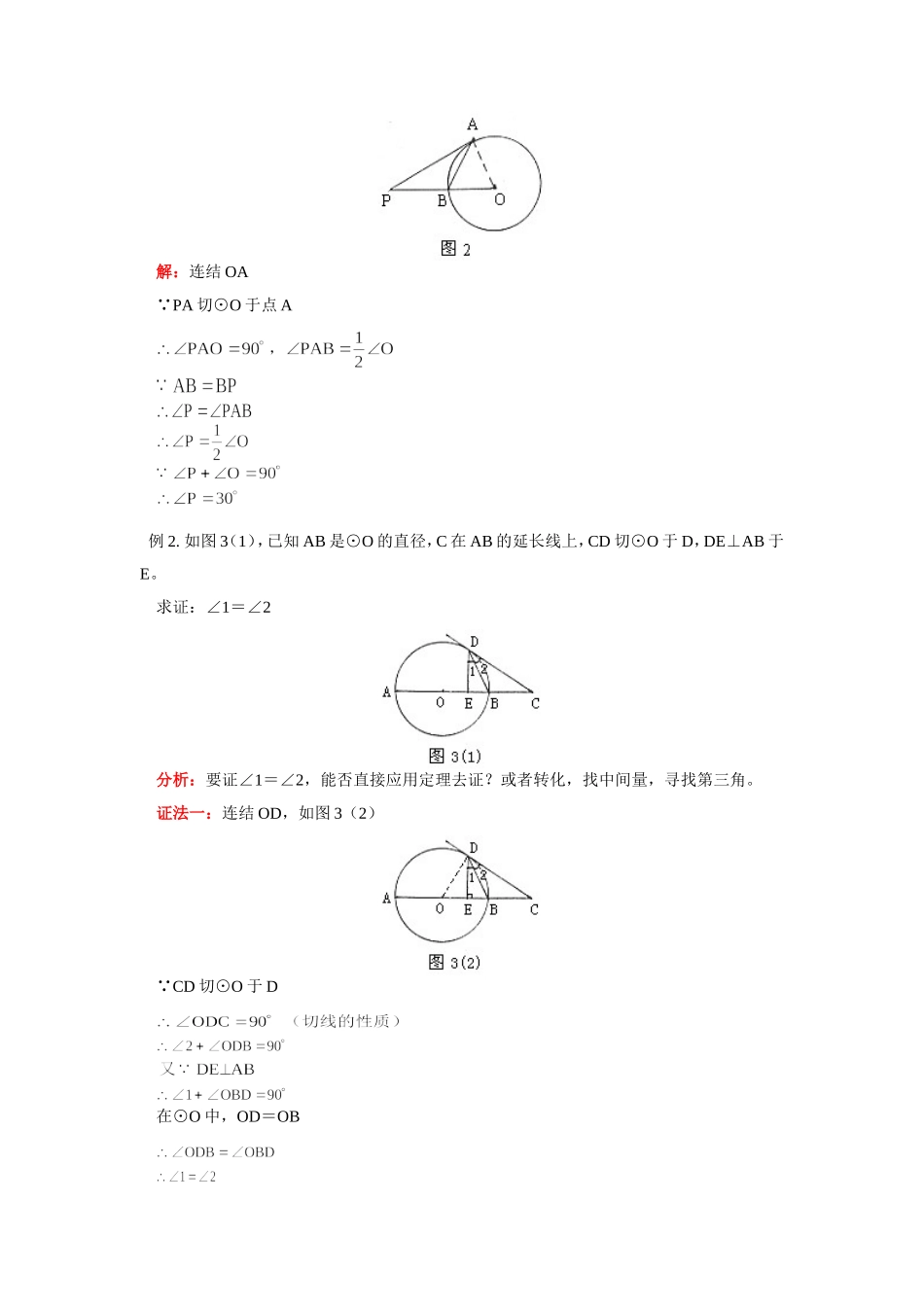
九年级数学弦切角、相交弦定理、割线定理、切割线定理首师大版【同步教育信息】一.本周教学内容:弦切角、相交弦定理、割线定理、切割线定理(一)弦切角:1.定义:顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角。满足三个条件:(1)顶点在圆上;(2)一边和圆相交;(3)一边和圆相切。判断下列图形中的∠BAC是不是弦切角:图A中,缺少“顶点在圆上”的条件;图B中,缺少“一边和圆相交”的条件;圆C中,缺少“一边和圆相切”的条件;圆D中,缺少“顶点在圆上”和“一边和圆相切”两个条件。所以,图中的∠BAC都不是弦切角。2.分类(以圆心的位置分):(1)圆心在角的外部;(2)圆心在角的一边上;(3)圆心在角的内部。3.弦切角的度理定理:弦切角的度数等于它所夹的弧的度数的一半。推论1:弦切角定理:弦切角等于它所夹的弧对的圆周角。推论2:在同圆或等圆中,如果两个弦切角所夹的弧相等,那么这两个弦切角也相等。(二)相交弦定理圆的两条弦相交,被交点分成的两条线段长的积相等。如图1(1),在⊙O中,AB、CD相交于点P,则PA·PB=PC·PD。(三)割线定理从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等。如图1(3),有PA·PB=PC·PD。(四)切割线定理从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。如图1(4),有PA2=PC·PD。当点P从圆内运动到圆上、圆外时(从图1(1)到图1(3)),总有PA·PB=PC·PD,图1(2)中,点B、D与点P重合,PB=PD=0,PA·PB=PC·PD同样成立。当割线PBA绕着点P旋转到切线PA的位置时,点B与A重合,结论不变,仍有PA·PB=PC·PD,此时PA=PB,所以PA2=PC·PD。当割线PDC也变为切线PC时,总有PA·PB=PC·PD,因为PC=PD,PA=PB,所以PA2=PC2,即PA=PC,此为切线长定理。当图1(1)中的两条相交弦的位置调整为:其中一条为直径,另一条弦与直径垂直,根据相交弦定理,同样有PA·PB=PC·PD,又根据垂径定理,有PA=PB,所以有PA2=PC·PD。在上面的图形变化中,点P的位置和AB、CD的位置在不断地变化,而变化中有不变量,即PA·PB=PC·PD的关系是不变的。我们应抓住图形的本质特征,我们把相交弦定理、割线定理、切割线定理统称为圆幂定理。二.重点、难点:重点是弦切角及其应用,相交弦、割线、切割线定理及其应用。难点是灵活应用三个定理证明等积线段问题,及三个定理之间的内在联系。【例题分析】例1.如图2,已知PA与⊙O切于点A,PO交⊙O于点B,AB=BP,求∠P的度数。解:连结OA PA切⊙O于点A例2.如图3(1),已知AB是⊙O的直径,C在AB的延长线上,CD切⊙O于D,DE⊥AB于E。求证:∠1=∠2分析:要证∠1=∠2,能否直接应用定理去证?或者转化,找中间量,寻找第三角。证法一:连结OD,如图3(2) CD切⊙O于D在⊙O中,OD=OB证法二:连结AD,如图3(3) AB是⊙O的直径又 CD切⊙O于D证法三:延长DE交⊙O于F,连结BF,如图3(4) AB是⊙O的直径,且AB⊥DF∴DB=BF则∠1=∠F CD是⊙O的切线∴∠2=∠F(弦切角定理)∴∠1=∠2证法四:过点B作⊙O的切线,交CD于M,如图3(5) AB是⊙O的直径∴AB⊥BM(切线的性质)又DE⊥AB∴DE∥MB∴∠1=∠DBM又 CD切⊙O于D∴∠2=∠MBD(弦切角定理推论)∴∠1=∠2证法五:连结OD,过B作BN⊥CD于N,如图3(6) CD切⊙O于D∴OD⊥CD(切线的性质)∴OD∥BN则∠ODB=∠DBN在⊙O中,OD=OB∴∠ODB=∠OBD∴∠DBN=∠OBD∴∠1=∠2(等角的余角相等)习题:由此题的各种解法可以得出圆中哪些常用的辅助线?如图3(7),学习过程中要不断总结经验,进行知识的归纳总结,从而得到提高。例3.已知AB是⊙O的弦,TA切⊙O于点A,∠TAB=110°,点C在圆周上,但与A、B两点不重合,求∠ACB的度数。分析:本题应分为两种情况,如图4(1)所示:所以,∠ACB的度数等于70°或110°例4.如图5(1),已知直线MN与以AB为直径的半圆相切于点C,∠A=28°。(1)求∠ACM的度数;(2)在MN上是否存在一点D,使AB·CD=AC·BC,为什么?分析:(1)由弦切角定理可得:∠ACM=∠B又AB是直径,∴∠B=90°-∠A而∠A已知,故∠ACM可...