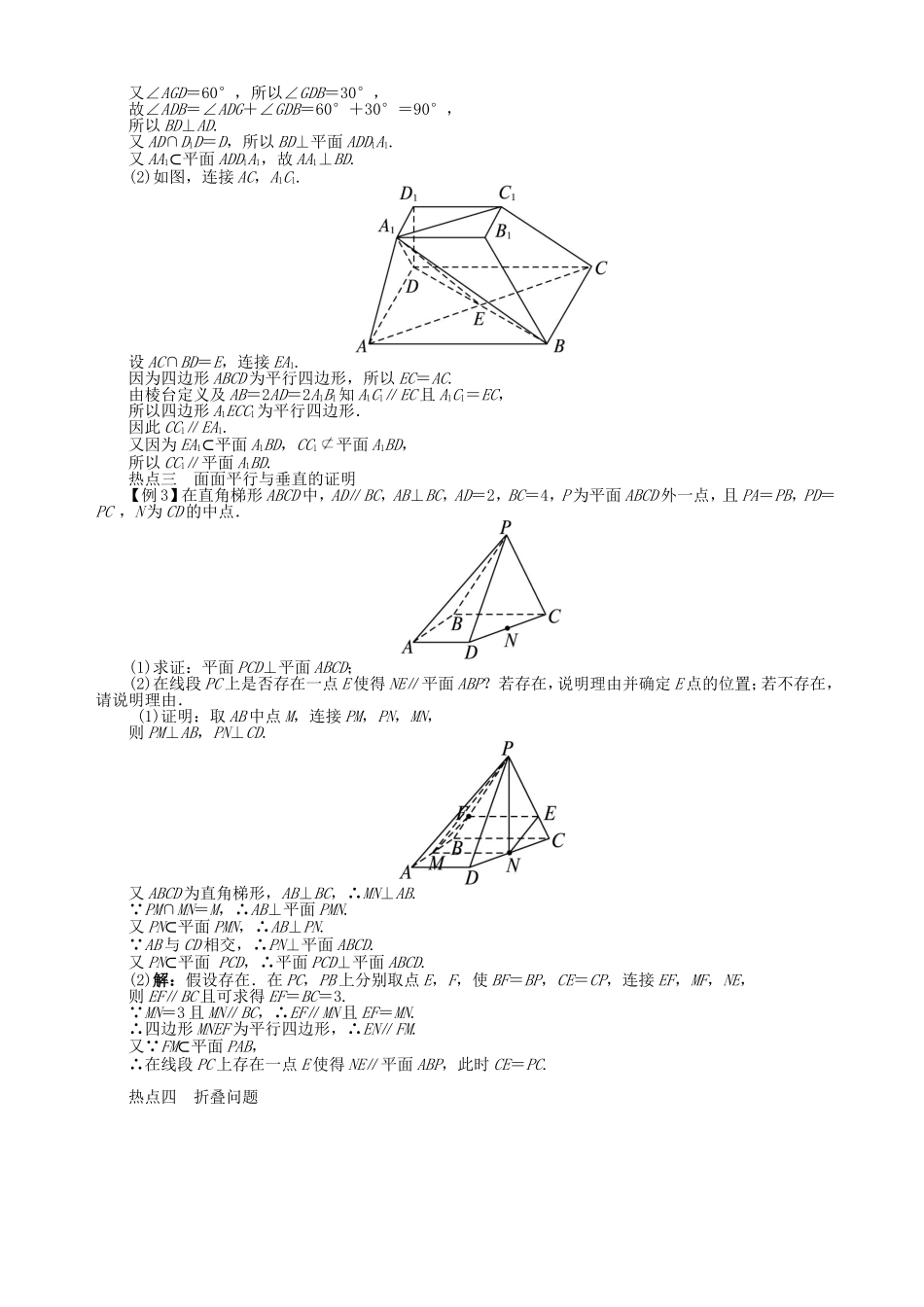
点、线、面的位置关系●知识梳理(一).平面公理1:如果一条直线上有两点在一个平面内,那么直线在平面内。公理2:不共线的三点确定一个平面.推论1:直线与直线外的一点确定一个平面.推论2:两条相交直线确定一个平面.推论3:两条平行直线确定一个平面.公理3:如果两个平面有一个公共点,那么它们还有公共点,这些公共点的集合是一条直线(二)空间图形的位置关系1.空间直线的位置关系:相交,平行,异面1.1平行线的传递公理:平行于同一条直线的两条直线互相平行。1.2等角定理:如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补。1.3异面直线定义:不同在任何一个平面内的两条直线——异面直线;1.4异面直线所成的角:(1)范围:;(2)作异面直线所成的角:平移法.2.直线与平面的位置关系:包含,相交,平行3.平面与平面的位置关系:平行,相交(三)平行关系(包括线面平行,面面平行)1.线面平行:①定义:直线与平面无公共点.②判定定理:③性质定理:2.线面斜交:①直线与平面所成的角(简称线面角):若直线与平面斜交,则平面的斜线与该斜线在平面内射影的夹角。范围:3.面面平行:①定义:;②判定定理:如果一个平面内的两条相交直线都平行于另一个平面,那么两个平面互相平行;符号表述:判定2:垂直于同一条直线的两个平面互相平行.符号表述:.③面面平行的性质:(1);(2)(四)垂直关系(包括线面垂直,面面垂直)1.线面垂直①定义:若一条直线垂直于平面内的任意一条直线,则这条直线垂直于平面。符号表述:若任意都有,且,则.②判定:③性质:(1);(2)BAO;3.2面面斜交①二面角:(1)定义:【如图】范围:②作二面角的平面角的方法:(1)定义法;(2)三垂线法(常用);(3)垂面法.3.3面面垂直(1)定义:若二面角的平面角为,则;(2)判定定理:(3)性质:①若,二面角的一个平面角为,则;②●热点例析【例1】热点一有关线面位置关系的组合判断若a,b是两条异面直线,α,β是两个不同平面,a⊂α,b⊂β,α∩β=l,则().A.l与a,b分别相交B.l与a,b都不相交C.l至多与a,b中一条相交D.l至少与a,b中的一条相交解析:假设l与a,b均不相交,则l∥a,l∥b,从而a∥b与a,b是异面直线矛盾,故l至少与a,b中的一条相交.选D.热点二线线、线面平行与垂直的证明【例2】如图,在四棱台ABCD-A1B1C1D1中,D1D⊥平面ABCD,底面ABCD是平行四边形,AB=2AD,AD=A1B1,∠BAD=60°.(1)证明:AA1⊥BD;(2)证明:CC1∥平面A1BD.(1)方法一:因为D1D⊥平面ABCD,且BD⊂平面ABCD,所以D1D⊥BD.又因为AB=2AD,∠BAD=60°,在△ABD中,由余弦定理得BD2=AD2+AB2-2AD·ABcos60°=3AD2,所以AD2+BD2=AB2.所以AD⊥BD.又AD∩D1D=D,所以BD⊥平面ADD1A1.又AA1⊂平面ADD1A1,故AA1⊥BD.方法二:因为D1D⊥平面ABCD,且BD⊂平面ABCD(如图),所以BD⊥D1D.取AB的中点G,连接DG(如图).在△ABD中,由AB=2AD得AG=AD.又∠BAD=60°,所以△ADG为等边三角形,因此GD=GB,故∠DBG=∠GDB.又∠AGD=60°,所以∠GDB=30°,故∠ADB=∠ADG+∠GDB=60°+30°=90°,所以BD⊥AD.又AD∩D1D=D,所以BD⊥平面ADD1A1.又AA1⊂平面ADD1A1,故AA1⊥BD.(2)如图,连接AC,A1C1.设AC∩BD=E,连接EA1.因为四边形ABCD为平行四边形,所以EC=AC.由棱台定义及AB=2AD=2A1B1知A1C1∥EC且A1C1=EC,所以四边形A1ECC1为平行四边形.因此CC1∥EA1.又因为EA1⊂平面A1BD,CC1平面A1BD,所以CC1∥平面A1BD.热点三面面平行与垂直的证明【例3】在直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=4,P为平面ABCD外一点,且PA=PB,PD=PC,N为CD的中点.(1)求证:平面PCD⊥平面ABCD;(2)在线段PC上是否存在一点E使得NE∥平面ABP?若存在,说明理由并确定E点的位置;若不存在,请说明理由.(1)证明:取AB中点M,连接PM,PN,MN,则PM⊥AB,PN⊥CD.又ABCD为直角梯形,AB⊥BC,∴MN⊥AB. PM∩MN=M,∴AB⊥平面PMN.又PN⊂平面PMN,∴AB⊥PN. AB与CD相交,∴PN⊥平面ABCD.又PN⊂平面PCD,∴平面PCD⊥平面ABCD.(2)解:假设存在.在PC,PB上分别取点E,F,使BF=BP,CE...