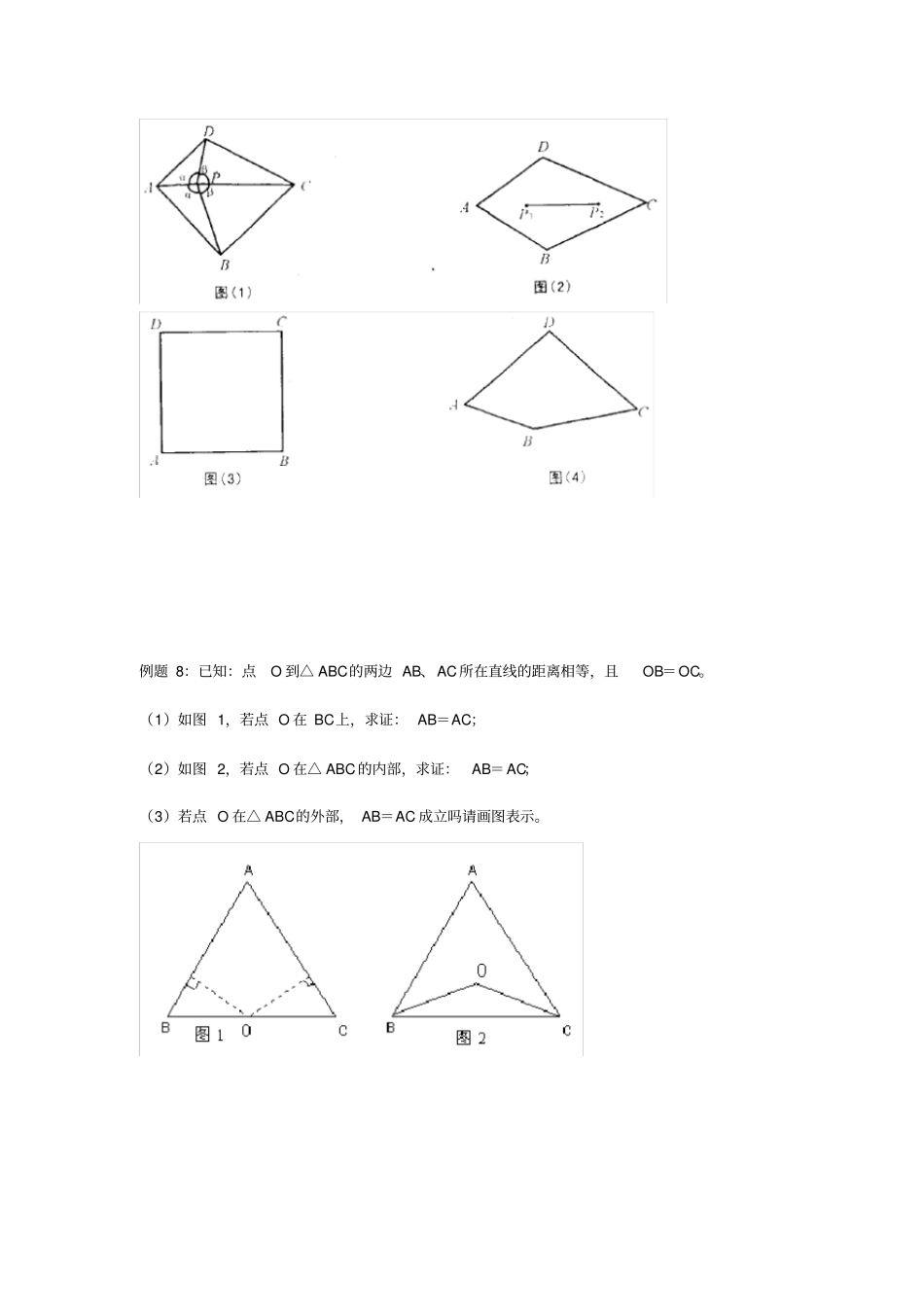
《三角形综合》例题1:AD,EF,BC相交于O点,且AO=OD,BO=OC,EO=OF.求证:△AEB≌△DFC例题2:P为正方形ABCD对角线BD上任一点,PF⊥DC,PE⊥BC.求证:AP⊥EF.例题3:△ABC的高AD与BE相交于H,且BH=AC.求证:∠BCH=∠ABC.例题4:在正方形ABCD中,P,Q分别为BC,CD边上的点,∠PAQ=45°.求证:PQ=PB+DQ.例题5:过△ABC的顶点A分别作两底角∠B和∠C的角平分线的垂线,AD⊥BD于D,AE⊥CE于E.求证:ED∥BC.例题6:如图,P是等边三角形ABC内部的一点,PA=2,PB=32,PC=4,求ΔABC的边长.例题7:如图(l),凸四边形ABCD,如果点P满足∠APD=∠APB=α。且∠BPC=∠CPD=β,则称点P为四边形ABCD的一个半等角点.(l)在图(3)正方形ABCD内画一个半等角点P,且满足α≠β。(2)在图(4)四边形ABCD中画出一个半等角点P,保留画图痕迹(不需写出画法).(3)若四边形ABCD有两个半等角点P1、P2(如图(2)),证明线段P1P2上任一点也是它的半等角点。例题8:已知:点O到△ABC的两边AB、AC所在直线的距离相等,且OB=OC。(1)如图1,若点O在BC上,求证:AB=AC;(2)如图2,若点O在△ABC的内部,求证:AB=AC;(3)若点O在△ABC的外部,AB=AC成立吗请画图表示。练习试题:1.如图,在ABC△中,ABC和ACB的平分线相交于点O,过点O作EFBC∥交AB于E,交AC于F,过点O作ODAC于D.下列四个结论:1902BOCA①°+;②以E为圆心、BE为半径的圆与以F为圆心、CF为半径的圆外切;③设ODmAEAFn,,则AEFSmn△;④EF不能成为ABC△的中位线.其中正确的结论是_____________.(把你认为正确结论的序号都填上)2.如图1,AB、CD是两条线段,M是AB的中点,DMCS、DACS和DBCS分别表示△DNC、△DAC、△DBC的面积。当AB∥CD时,有DMCS=2DBCDACSS(1)(1)如图2,若图1中AB与CD不平行时,(1)式是否成立请说明理由。(2)如图3,若图1中AB与CD相交于点O时,DMCS、DACS和DBCS有何种相等关系试证明你的结论。图1MBDCA图2MBDCAO图3MBDCA3.如图,设△ABC和△CDE都是正三角形,且∠EBD=62o,则∠AEB的度数是【】(A)124o(B)122o(C)120o(D)118o4.如图,△ABC是等边三角形,△BDC是顶角∠BDC=120°的等腰三角形,M是AB延长线上一点,N是CA延长线上一点,且∠MDN=60°.试探究MB、MN、CN之间的数量关系,并给出证明.5.如图,在△ABC中,∠ABC=600,点P是△ABC内的一点,使得∠APB=∠BPC=∠CPA,且PA=8,PC=6,则PB=_____________ABCP6.如图所示,在△ABC中,AB=AC,AD=AE,60BAD,则EDC__________7.(1)如图7,点O是线段AD的中点,分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形OCD,连结AC和BD,相交于点E,连结BC.求∠AEB的大小;(2)如图8,ΔOAB固定不动,保持ΔOCD的形状和大小不变,将ΔOCD绕着点O旋转(ΔOAB和ΔOCD不能重叠),求∠AEB的大小.8.两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,BCE,,在同一条直线上,连结DC.(1)请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母);(2)证明:DCBE.9.如图,AD是△ABC的边BC上的高,由下列条件中的某一个就能推出△ABC是等腰三角形的是__________________。(把所有正确答案的序号都填写在横线上)①∠BAD=∠ACD②∠BAD=∠CAD,③AB+BD=AC+CD④AB-BD=AC-CD参考答案例题1、证明:△OAE≌△ODF,因为:二边及夹角(对等角)相等,得:AE=DF。同理证得:△OBE≌△OCF,△OAB≌△OCD,得:EB=CF,AB=CD。因为:AE=DF,EB=CF,AB=CD三边相等。所以:△AEB≌△DFC例2F于点G延长EP交AB于M,延长FP交AD于N P为正方形ABCD对角线BD上任一点∴PM=PF,PN=PE又AMPN为矩形.∴AN=PM=PF ∠EPF=∠BAC=90°∴△PEF≌△ANP∴∠NAP=∠PFE又∠NPA=∠FPG(对顶角)∠NAP+∠NPA=90°∴∠PFE+∠FPG=90°∴∠PGF=180°-(∠PFE+∠FPG)=90°∴AP⊥EF例3 BH=AC,∠BDH=∠ADC=90°,∠HBD=∠CAD(这个知道的吧)∴△BDH≡△ADC∴HD=CD,BD=AD∴△HDC与△ABD是等腰直角三角形∴∠BCH=∠ABD=45°例4:在CB的延长线上取点G,使BG=DQ,连接AG 正方形ABCD∴AB=A...