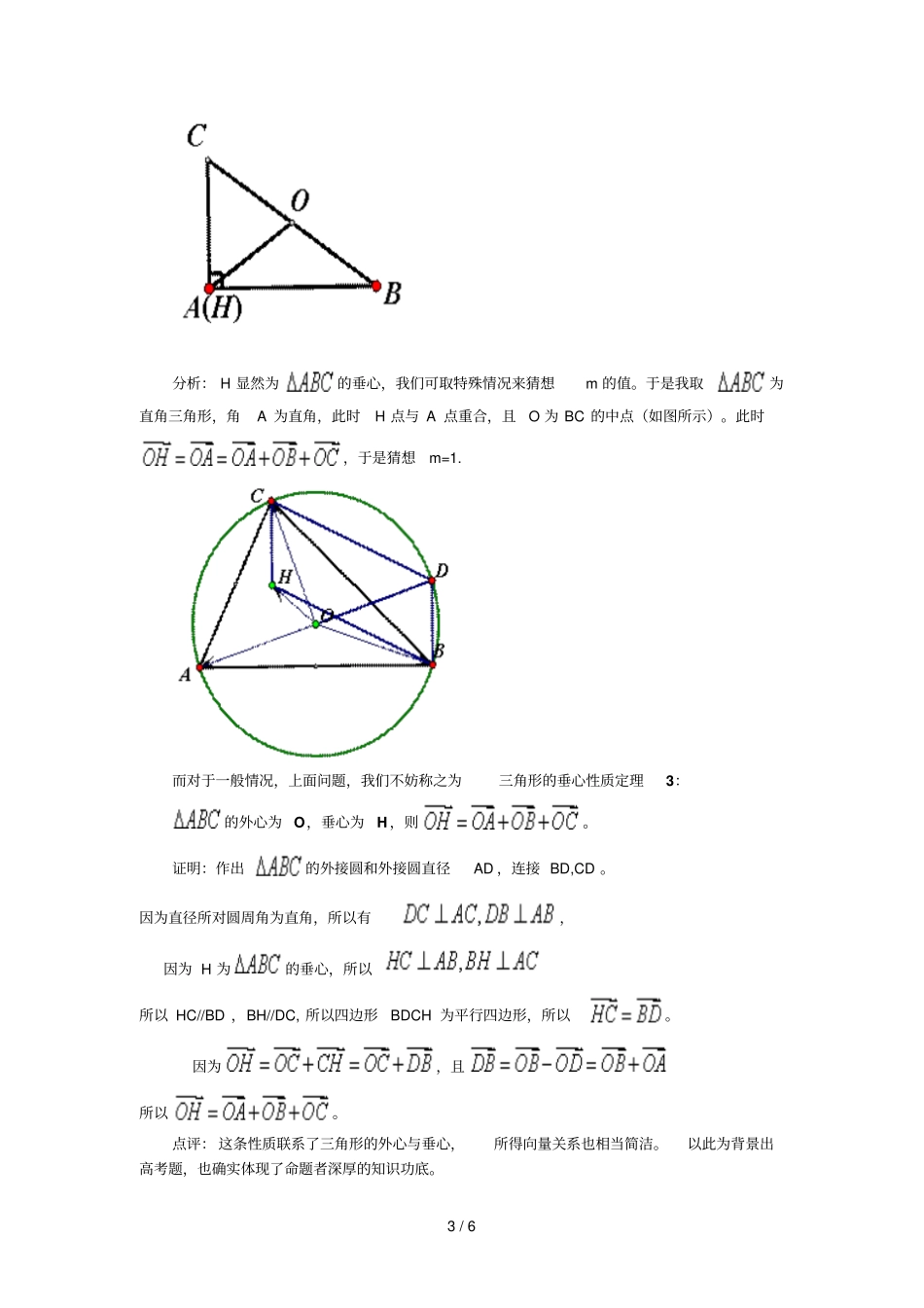
1/6三角形垂心的性质总结山西省原平市第一中学任所怀三角形的垂心定理:在三角形ABC中,求证:它的三条高交于一点。证明:如图:作BE于点E,CFAB于点F,且BE交CF于点H,连接AH并延长交BC于点D。现在我们只要证明ADBC即可。因为CFAB,BE所以四边形BFEC为圆内接四边形。四边形AFHE为圆内接四边形。所以∠FAH=∠FEH=∠FEB=∠FCB由∠FAH=∠FCB得四边形AFDC为圆内接四边形所以∠AFC=∠ADC=90°即ADBC。点评:以上证明主要应用了平面几何中的四点共圆的判定与性质。三角形垂心的性质定理1:锐角三角形的垂心是以三个垂足为顶点的三角形的内心。如上图,在三角形ABC中,AD、CF、BE分别为BC、AB、AC上的高,D、F、E分别为垂足,H为三角形ABC的垂心。求证:H为三角形DFE的内心。证明:要证H为三角形DFE的内心,只需证明HF、HE、HD分别平分∠DFE、∠FED、∠EDF。同样我们还是利用四点共圆的判定与性质来证明。由BCEF四点共圆得∠EFC=∠EBC(都是弧CE所对的圆周角)由HFBD四点共圆得∠HFD=∠HBD=∠EBC(都是弧HD所对的圆周角)所以∠EFH=∠HFD所以HF平分∠EFD。同理HE平分∠FED;HD平分∠FDE所以H为三角形DFE的内心。点评:以上两个问题都用到了四点共圆。因为在这个图形中共可得到6个圆内接四边形,你不妨找一找。三角形垂心的向量表示:在中,若点O满足,则点O为三角形ABC的垂心。2/6证明:由得,所以。同理OB,,则点O为垂心。三角形垂心性质定理2:若三角形的三个顶点都在函数的图象上,则它的垂心也在这个函数图象上。证明:设点O(x,y)为的垂心,则上面的向量表示得因为的三个顶点都在函数的图象上,所以设,因为,所以所以所以(1)同理:由得(2)联立(1)(2)两式,就可解出显然有垂心O在函数的图象上。点评:此题恰当地应用了垂心的向量表示,把几何问题转化成了代数问题,完美体现了数形结合的数学思想。(2005年全国一卷理科)的外接圆的圆心为O,两条边上的高的交点为H,,则实数m=3/6分析:H显然为的垂心,我们可取特殊情况来猜想m的值。于是我取为直角三角形,角A为直角,此时H点与A点重合,且O为BC的中点(如图所示)。此时,于是猜想m=1.而对于一般情况,上面问题,我们不妨称之为三角形的垂心性质定理3:的外心为O,垂心为H,则。证明:作出的外接圆和外接圆直径AD,连接BD,CD。因为直径所对圆周角为直角,所以有,因为H为的垂心,所以所以HC//BD,BH//DC,所以四边形BDCH为平行四边形,所以。因为,且所以。点评:这条性质联系了三角形的外心与垂心,所得向量关系也相当简洁。以此为背景出高考题,也确实体现了命题者深厚的知识功底。4/6三角形垂心性质定理3:三角形任一顶点到垂心的距离,等于外心到对边的距离的2倍。即:的外心为O,垂心为H,D为BC中点,则AH=2OD。证明:因为D为BC中点所以由性质2知:得所以AH=2OD。点评:性质定理3,也可看做是性质定理2的推论。三角形垂心性质定理4:锐角三角形的垂心到三顶点的距离之和等于其内切圆与外接圆半径之和的2倍。分析:应用上面的性质定理3,上面这一结论可改为锐角三角形的外接圆与内切圆径之和等于外心到三角形三边距离之和。即:如图在锐角中,O为外心,D,E,F分别为三边的中点。设外接圆半径为R,内切圆半径为r,则OD+OE+OF=R+r.证明:在锐角中,O为外心,D,E,F分别为三边的中点,则OF,,5/6所以有=设中角A,B,C所对边的长分别为a,b,c.在圆O中,弧AB所对的圆心角=2C又因OA=OB,OF,所以OF=OA*cosC=RcosC。同理OD=R*cosB,OE=R*cosA所以而由三角形内切圆的性质知:所以这个式子就指出了内切圆半径与外接圆半径的关系。而要证OD+OE+OF=R+r,需证:RcosA+RcosB+RcosC=R+即需证需证(b+c)cosA+(a+c)cosB+(a+b)cosC=a+b+c而对上式的证明我们可采用正弦定理,化角为边,即需证:sinBcosA+sinCcosA+sinAcosB+sinCcosB+sinAcosC+sinBcosC=sinA+sinB+sinC需证:sin(A+B)+sin(A+C)+sin(B+C)=sinA+sinB+sinC而因为A+B+C=所以sin(A+B)+sin(A+C)+sin(B+C)=sinA+sinB+sinC显然成立所以命题得证。点评:此题的证明充分联系我们初高中的大量知识,真是做到了“八方联系,浑然一体”(孙维刚老师语)。通过这样的一个问题,我们的数学能力将大大...