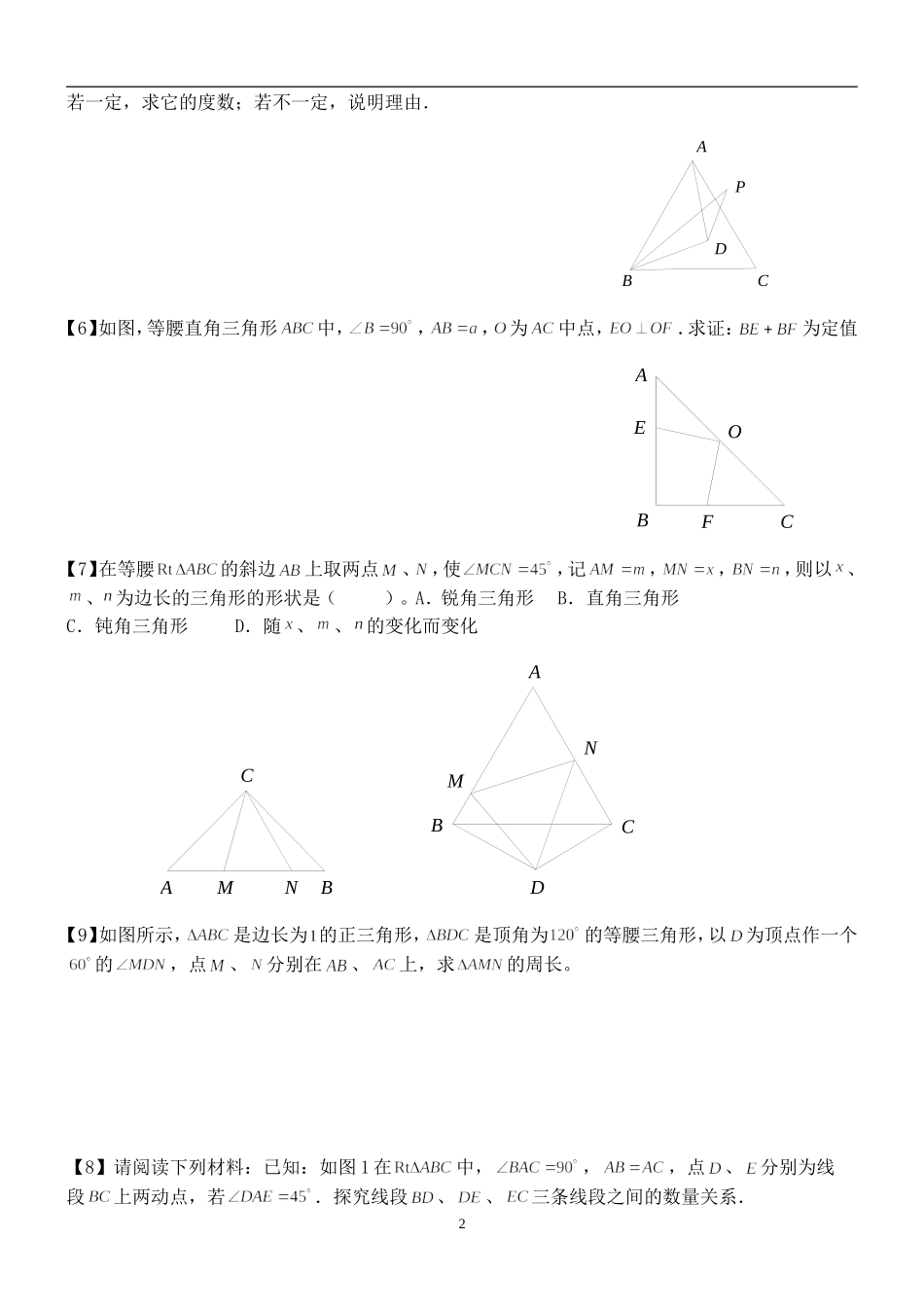
1七年级数学下---全等三角形【1】如图,点为线段上一点,、是等边三角形.请你证明:⑴;⑵;⑶平分.MDNECBFA【2】如图,点为线段上一点,、是等边三角形,是中点,是中点,求证:是等边三角形.MDNECBA【3】如下图,在线段同侧作两个等边三角形和(),点与点分别是线段和的中点,则是_____________。A.钝角三角形B.直角三角形C.等边三角形D.非等腰三角形PMBCDEADECBA【4】如图,等边三角形与等边共顶点于点.求证:.【5】如图,是等边内的一点,且,,,问的度数是否一定,2若一定,求它的度数;若不一定,说明理由.PDCBA【6】如图,等腰直角三角形中,,,为中点,.求证:为定值OBECFA【7】在等腰的斜边上取两点、,使,记,,,则以、、为边长的三角形的形状是()。A.锐角三角形B.直角三角形C.钝角三角形D.随、、的变化而变化MNCBANMDCBA【9】如图所示,是边长为的正三角形,是顶角为的等腰三角形,以为顶点作一个的,点、分别在、上,求的周长。【8】请阅读下列材料:已知:如图1在中,,,点、分别为线段上两动点,若.探究线段、、三条线段之间的数量关系.3小明的思路是:把绕点顺时针旋转,得到,连结,使问题得到解决.请你参考小明的思路探究并解决下列问题:⑴猜想、、三条线段之间存在的数量关系式,并对你的猜想给予证明;⑵当动点在线段上,动点运动在线段延长线上时,如图2,其它条件不变,⑴中探究的结论是否发生改变?请说明你的猜想并给予证明.图1ABCDE图2ABCDE【12】平面上三个正三角形,,两两共只有一个顶点,求证:与平分.FEDBCA【10】在等边的两边AB,AC所在直线上分别有两点M,N,D为外一点,且,,,探究:当点M,N分别爱直线AB,AC上移动时,BM,NC,MN之间的数量关系及的周长与等边的周长L的关系。4⑴如图①,当点M,N在边AB,AC上,且DM=DN时,BM,NC,MN之间的数量关系式__________;此时=__________⑵如图②,当点M,N在边AB,AC上,且时,猜想(1)问的两个结论还成立吗?写出你的猜想并加以证明;⑶如图③,当点M,N分别在边AB,CA的延长线上时,若AN=x,则Q=_________(用x,L表示)【13】已知:如图,、、都是等边三角形,且、、共线,.求证:也是等边三角形.EKHCDBA5MABDCHKE【11】(1)如图,在四边形ABCD中,AB=AD,∠B=∠D=,E、F分别是边BC、CD上的点,且∠EAF=∠BAD.求证:EF=BEFD。FEDCBA(2)如图,在四边形ABCD中,AB=AD,∠B+∠D=,E、F分别是边BC、CD上的点,且∠EAF=∠BAD,(1)中的结论是否仍然成立?不用证明.FEDCBA【14】如图所示,在五边形中,,,求此五边形的面积。6【15】在五边形中,已知,,,连接.求证:平分.EDCBA【16】如图,已知和都是等边三角形,、、在一条直线上,试说明与相等的理由.EDCBA【17】在梯形中,,,,,,是中点,试判断与的位置关系,并写出推理过程.7ABCDE【18】在等腰直角中,,,是的中点,点从出发向运动,交于点,试说明的形状和面积将如何变化.APMCQB【19】等边和等边的边长均为1,是上异于的任意一点,是上一点,满足,当移动时,试判断的形状.DFECBA答案:【1】⑴ 、是等边三角形,∴,,∴,∴;⑵由易推得,所以,又,进而可得为等边三角形.易得.⑶过点作于,于,由;利用进而再证,可得,故平分.【2】 ,∴,;又 、分别是、的中点,∴,∴,;∴;∴是等边三角形【3】易得.所以可以看成是绕着点顺时针旋转而得到的.又为线段中点,为线段中点,故就是绕着点顺时针旋转而得.所以且,,故是等边三角形,选C.8【4】 是等边三角形,∴,.∴,同理,.∴在与中,∴,∴.【5】连接,将条件,这两个条件,易得(),得,由,,(公共边),知(),∴.故的度数是定值.ABCDP4321OBECFAMDNCBA【6】连结由上可知,,,,而,.∴,∴,∴.【7】如图,将绕点顺时针旋转,得,连结,则,,,∴.∴,∴又易得,∴在中,有,故应选(B)【8】⑴证明:根据绕点顺时针旋转得到;∴∴,,,;在中; ;∴;∴;即;∴;又 ;∴;∴;即;∴;∴;∴;E'EDCBAFEDCBA⑵关系式仍然成立;证明:将沿直线对折,得,连∴;∴,;,;又 ,∴; ;9;∴;又 ;∴;∴,;;∴;...