椭圆的简单几何性质用VIP免费

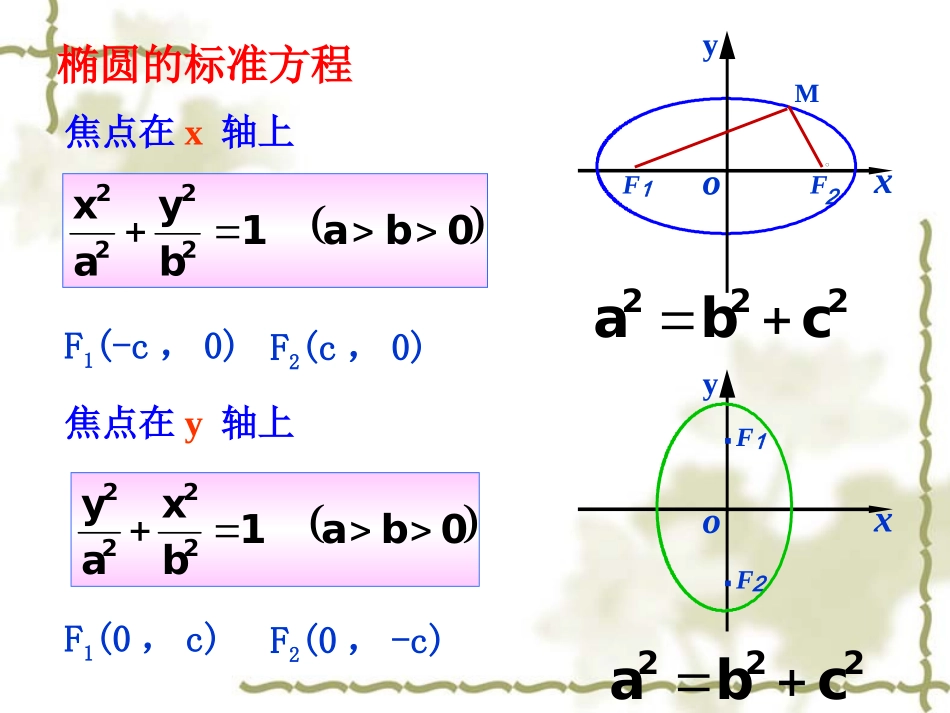
2.2.2椭圆的简单几何性质0ba1byax2222焦点在x轴上12yoFFMx222cba椭圆的标准方程0ba1bxay2222焦点在y轴上222cbayo1FF2x..F1(-c，0)F2(c，0)F1(0，c)F2(0，-c)Ax2＋By2＝1（A＞0，B＞0，A≠B）椭圆的一般方程一、椭圆的范围即-a≤x≤a-b≤y≤b结论：椭圆位于直线x＝±a和y＝±b围成的矩形里．oxy-aab-b22222222111xyxyabab由和xayb即：和yOF1F2x二、椭圆的对称性结论：椭圆既是轴对称图形，又是中心对称图形对称轴是x轴和y轴，对称中心是原点中心：椭圆的对称中心叫做椭圆的中心小试身手：1.已知点P(3，6)在上,则()22221xyab(A)点(-3,-6)不在椭圆上(B)点(3,-6)不在椭圆上(C)点(-3,6)在椭圆上(D)无法判断点(-3,-6),(3,-6),(-3,6)是否在椭圆上C三、椭圆的顶点顶点：椭圆与它的对称轴的四个交点，叫做椭圆的顶点。oxyB1(0,b)B2(0,-b)A1(-a,0)A2(a,0)令x=0,得y=？说明椭圆与y轴的交点为(0,b)、(0,-b)2222xy+=1(a>b>0)ab令y=0,得x=？说明椭圆与x轴的交点为(a,0)、(-a,0)三、椭圆的顶点长轴、短轴：线段A1A2、B1B2分别叫做椭圆的长轴和短轴。oxyB1(0,b)B2(0,-b)A1A2a、b分别叫做椭圆的长半轴长和短半轴长。思考：椭圆的焦点与椭圆的长轴、短轴有什么关系？焦点落在椭圆的长轴上长轴：线段A1A2；长轴长|A1A2|=2a短轴：线段B1B2；短轴长|B1B2|=2b焦距|F1F2|=2c①①aa和和bb分别叫做椭圆的分别叫做椭圆的长半轴长和短半轴长；长半轴长和短半轴长；③③焦点必在长轴上；焦点必在长轴上；②a2=b2+c2，oxyB2(0,b)B1(0,-b)A2(a,0)A1(-a,0)bac椭圆的简单几何性质aF2F1|B2F2|=a；注意注意由椭圆的范围、对称性和顶点，再进行描点画图，只须描出较少的点，就可以得到较正确的图形.小结：离心率：椭圆的焦距与长轴长的比ce=a椭圆的离心率．,叫做四、椭圆的离心率[1]离心率的取值范围：因为a>c>0，所以00a>c>0ceaxyＯA2(a,0)A1(-a,0)B2(0,b)B1(0,-b)一个框，四个点，注意光滑和圆扁,莫忘对称要体现．课堂小结课堂小结用曲线的图形和方程用曲线的图形和方程)0(12222babyax来研究来研究椭圆的简单几何性质椭圆的简单几何性质小试身手：2.说出椭圆的范围,长轴长,短轴长,焦点坐标,顶点坐标:221916xy33,44xy28,26ab(0,7)(0,4),(3,0)例１求椭圆16x2+25y2=400的长轴和短轴的长、离心率、焦点和顶点坐标并画出简图．解：把已知方程化成标准方程1452222yx这里，31625,4,5cba椭圆的长轴长和短轴长分别是82,102ba离心率6.053ace四个顶点坐标分别为)4,0(),4,0(),0,5(),0,5(2121BBAA焦点坐标分别为0,3,0,321FF基本量：a、b、c、e、（共四个量）基本点：四个顶点、两个焦点（共六个点）练习求经过点P(4,1)，且长轴长是短轴长的2倍的椭圆的...