知识精讲高二数学9.1～9.4阶段性复习人教版VIP免费

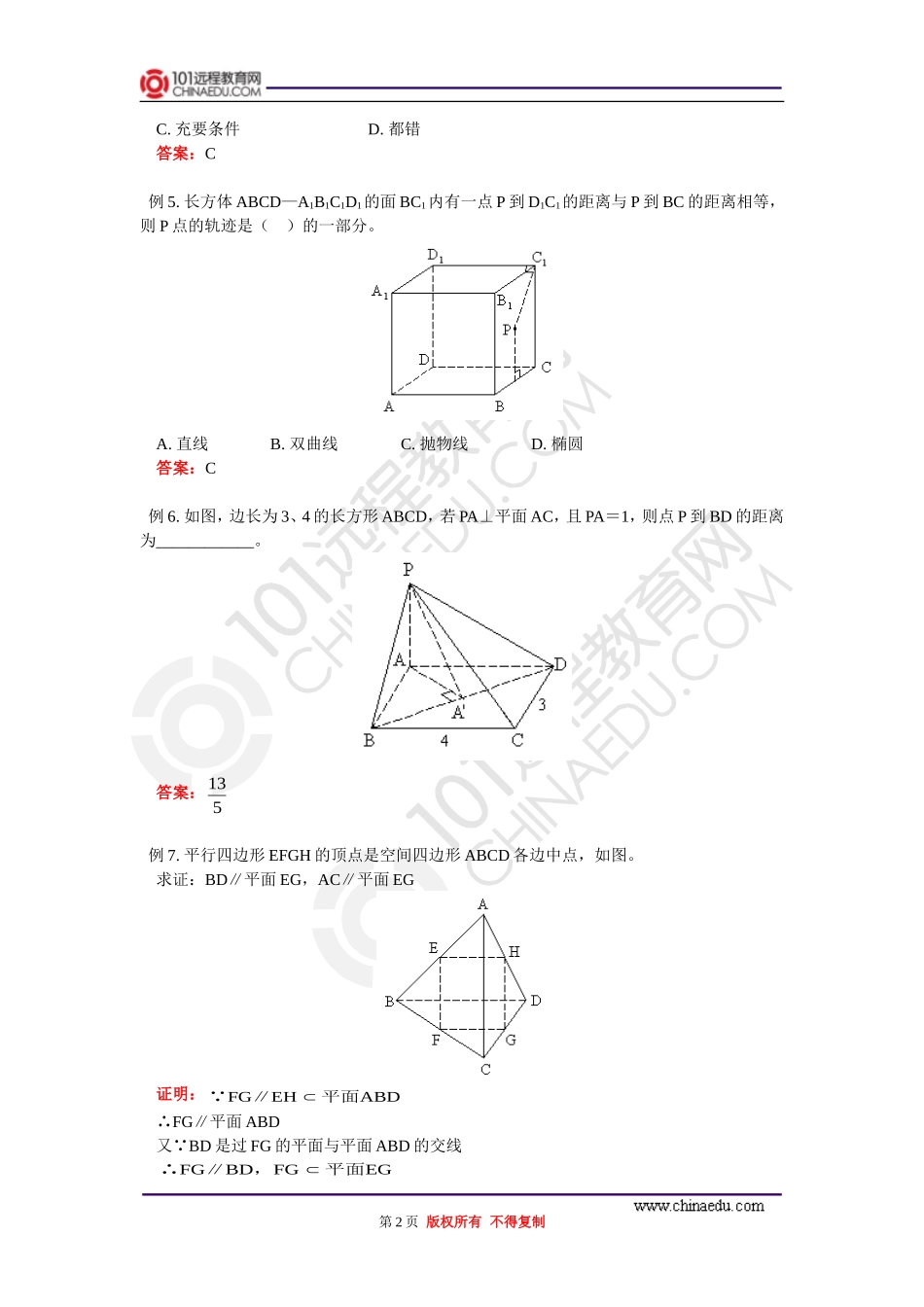
高二数学9.1～9.4阶段性复习人教版【本讲教育信息】一.教学内容：9.1～9.4阶段性复习【典型例题】例1.如图，在正方体中，与，与所成角是ABCDABCDDBADADAC1111111（）A.45°，60°B.90°，60°C.45°，60°D.60°，60°解：ADADABAD111⊥，⊥平面ADDB11⊥又 为正三角形ADC11∴选B例2.若两条异面直线所成角为60°，那么，过空间一点只能作一条直线与这两条异面直线所成角相等为θ，则θ值为（）A.90°B.30°C.60°D.90°或30°答案：D例3.设点P是△ABC所在平面α外的一点，点O是P在α内的射影，若PA＝PB＝PC，则点O是△ABC的__________。答案：外心注：若PA⊥PB⊥PC，PA⊥PC，O为垂心。若P到△ABC三边距离相等，O为内心。例4.已知平面α、β，直线a、b，若α∥β，a∥b，则a⊥α是b⊥β的（）A.充分不必要条件B.必要不充分条件第1页版权所有不得复制C.充要条件D.都错答案：C例5.长方体ABCD—A1B1C1D1的面BC1内有一点P到D1C1的距离与P到BC的距离相等，则P点的轨迹是（）的一部分。A.直线B.双曲线C.抛物线D.椭圆答案：C例6.如图，边长为3、4的长方形ABCD，若PA⊥平面AC，且PA＝1，则点P到BD的距离为____________。答案：135例7.平行四边形EFGH的顶点是空间四边形ABCD各边中点，如图。求证：BD∥平面EG，AC∥平面EG证明： ∥平面FGEHABD∴FG∥平面ABD又 BD是过FG的平面与平面ABD的交线∴∥，平面FGBDFGEG第2页版权所有不得复制于是，BD∥平面EG同理可证AC∥平面EFGH例8.已知平行四边形ABCD在平面α的同侧，求证：ABCD在平面α内的射影是平行四边形。证明：设A’B’C’D’是ABCD在α内射影，则AA’、BB’、CC’、DD’均与α垂直∴AA’∥BB’∥CC’∥DD’又 AB∥CD，AD∥BC∴平面AB’∥平面DC’于是，A’B’∥C’D’同理可证：A’D’∥B’C’∴A’B’C’D’为平行四边形例9.在正方体ABCD—A1B1C1D1中，P、Q、R分别是A1B1、C1C与AD的中点。求证：D1B⊥平面PQR证：可先证BD1⊥平面ACB1（略）再证，平面PQR∥平面ACB1取AB1中点EPEQCPQECACB//，∴∥平面1同理可证：∥（为中点）PRBOOAC1∴平面∥平面PQRACB1于是，⊥平面BDACB11例10.如图，E、F、G、H分别是正方体AA1、AB、BC、DD1的中点。求证：直线HB⊥平面B1FG第3页版权所有不得复制证明：FGACDBHDACFGBH∥⊥⊥平面⊥1又 ⊥⊥平面⊥BFEBHEABHBFB1112由：⊥平面121HBBFG【模拟试题】一.选择题（每小题5分，共40分）1.下面四个条件中，不能确定一个平面的是（）A.一个圆上的三个点B.一条直线和一个点C.两条相交直线D.两条平行直线2.水平放置的正方形ABCD的边长为1，其斜二测画法的直观图A’B’C’D’的面积是（）A.28B.12C.22D.243.已知两条直线a、b和两异面直线c、d都相交，则直线a、b的位置关系是（）A.相交B.平行C.异面D.相交或异面4.若∠ABC＝∠A’B’C’，且BA∥B’A’，BA与B’A’的方向相同，则下列结论中正确的是（）A.BC∥B’C’且方向相同B.BC∥B’C’且方向相反C.BC与B’C’不平行D.BC与B’C’不一定平行5.已知m、n是不重合的直线，α、β是不重合的平面，有下列命题：①若m∥n，n，则m∥；②若m∥α，n，则m∥n；③若m⊥α，n⊥α，则m∥n；④若m⊥α，m⊥β，则α∥β。其中真命题的个数是（）A.0B.1C.2D.36.在正方体ABCDABCD1111的六个面的对角线中，与AC异面且成60°角的直线有（）第4页版权所有不得复制A.4条B.6条C.8条D.10条7.如图1，定点A和B都在平面α内，定点P在α外，PB⊥α，C是α内异于A和B的动点，且PC⊥AC，那么动点C在平面α内的轨迹是（）图1A.一条线段，但要去掉两个点B.一个圆，但要去掉两个点C.一个椭圆，但要去掉两个点D.半圆，但要去掉两个点8.正方体AC1中，M是棱DD1的中点，O是正方形ABCD的中心，则异面直线OA1与AM所成的角是（）A.90°B.60°C.45°D.以上答案都不对二.填空题（每小题4分，共16分）9.两两相交的三条直线可以确定__________个平面。10.已知空间四边形ABCD中，AB＝CD＝3，E、F分别是线段AD、BC上的点，且AE∶ED＝BF∶FC＝1∶2，EF7，则AB与CD所成角的大小是__________。11.如图2，ABCD是一个平面截长方体所得的截面，...