高二数学期末复习（二）人教版知识精讲知识精讲VIP免费

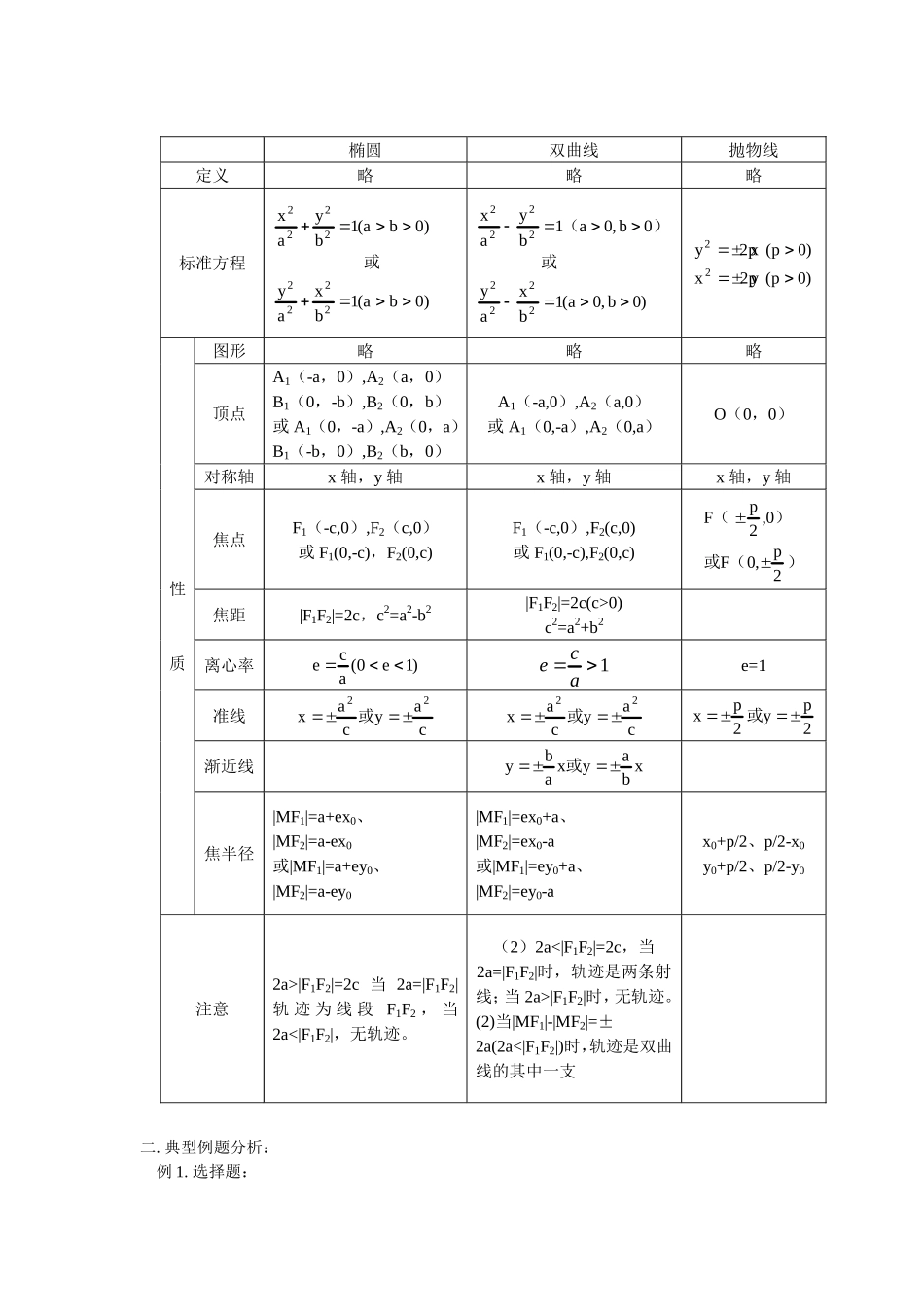
高二数学期末复习（二）人教版【同步教育信息】一.本周教学内容：《期末复习》（二）教学目标：较好地掌握圆锥曲线的定义，标准方程，几何性质，并会灵活运用。掌握一定的解题技巧和数学思想方法。注意培养和训练自己的计算能力；恒等变形能力；数形结合能力；分类讨论能力；逻辑推理能力；综合分析问题和解决问题的能力。重点：圆锥曲线的定义，标准方程，几何性质等知识的理解和记忆，求圆锥曲线的常用的思想方法。直线与圆锥曲线相交后求弦长问题，求解与弦中点相关的问题。难点：用定义法求轨迹方程。圆锥曲线的标准方程各种不同形式的区别及性质的区别；圆锥曲线的标准方程和几何性质在解题中的综合运用。常考知识点拨：圆锥曲线在高考中占有较大比例和重要地位，重点考查它的定义，标准方程。几何性质及相关知识的综合应用。考试题型有：选择题、填空题、解答题三种形式，特别是大题必有一道。知识总结知识体系表解椭圆双曲线抛物线定义略略略标准方程)0ba(1bxay)0ba(1byax22222222或xaybabyaxbab22222222100100（）或,(,))0p(py2x)0p(px2y22图形略略略顶点A1（-a，0）,A2（a，0）B1（0，-b）,B2（0，b）或A1（0，-a）,A2（0，a）B1（-b，0）,B2（b，0）A1（-a,0）,A2（a,0）或A1（0,-a）,A2（0,a）O（0，0）对称轴x轴，y轴x轴，y轴x轴，y轴焦点F1（-c,0）,F2（c,0）或F1(0,-c)，F2(0,c)F1（-c,0）,F2(c,0)或F1(0,-c),F2(0,c)FpFp（）或（）2002,,焦距|F1F2|=2c，c2=a2-b2|F1F2|=2c(c>0)c2=a2+b2离心率)1e0(ace1acee=1准线caycax22或caycax22或xpyp22或渐近线xbayxaby或性质焦半径|MF1|=a+ex0、|MF2|=a-ex0或|MF1|=a+ey0、|MF2|=a-ey0|MF1|=ex0+a、|MF2|=ex0-a或|MF1|=ey0+a、|MF2|=ey0-ax0+p/2、p/2-x0y0+p/2、p/2-y0注意2a>|F1F2|=2c当2a=|F1F2|轨迹为线段F1F2，当2a<|F1F2|，无轨迹。（2）2a<|F1F2|=2c，当2a=|F1F2|时，轨迹是两条射线；当2a>|F1F2|时，无轨迹。(2)当|MF1|-|MF2|=±2a(2a<|F1F2|)时，轨迹是双曲线的其中一支二.典型例题分析：例1.选择题：1.θ是任意实数，则方程x2+y2sinθ=4的曲线不可能是（）A.椭圆B.双曲线C.抛物线D.圆2.已知抛物线y2=2px，（P>0）上有一点M（4，y），它到焦点F的距离为5，O为原点，则△OFM的面积为（）A.1B.2C.2D.22341122212.设、为双曲线的两个焦点，点在双曲线上且满足FFxyPFPF90°，则△F1PF2的面积为（）ABCD....15225439412.||直线与曲线的交点个数是（）yxyxxA.0B.1C.2D.3解1：为任意实数11sin当时，方程为：，两条直线sin0422xx当时，方程为：，为圆sin1422xy当时，方程为：，为等轴双曲线sin1422xy当时，方程：为椭圆011122sinsinxy当时，方程：为双曲线101122sinsinxy∴不论θ为何值，曲线都不可能是抛物线。∴选（C）。解2：利用抛物线定义：||MFpp42524，yxMy244，（，）yy244164，SOFM12142选（）C解3：由双曲线方程xy2241知：，，abc215设，，||||PFmPFnSmnFFP121212()()222222cmnmnmn20162mnmn2SmnAFPF12121221选（）yPF1OF2x解4：曲线方程化为：xyxxyx094109412222时，时，曲线的图形是左半个椭圆和上、下各半支双曲线组合而成又的斜率为yx31渐近线的斜率为：941943yx与渐近线相交yx3与曲线上方还有一个交点。应选（）Dy3-312x例2.填空题：1.双曲线与椭圆4x2+y2=64有相同的焦点，它的一条渐近线为y=x，则双曲线的标准方程为_________________2.过点P（0，4）与抛物线y2=2x只有一个公共点的直线有___________条。3.y=kx+1x直线与焦点在轴上的椭圆总有公共点，则的取值范xymm2251围是___________4.过点M（-2，0）的直线与椭圆x2+2y2=2交于P1、P2两点，线段P1P2的中点P，设直线l的斜率为k1(k1≠0)，直线OP的斜率为k2，则k1·k2的值为____________。解1：求出椭圆的焦点...