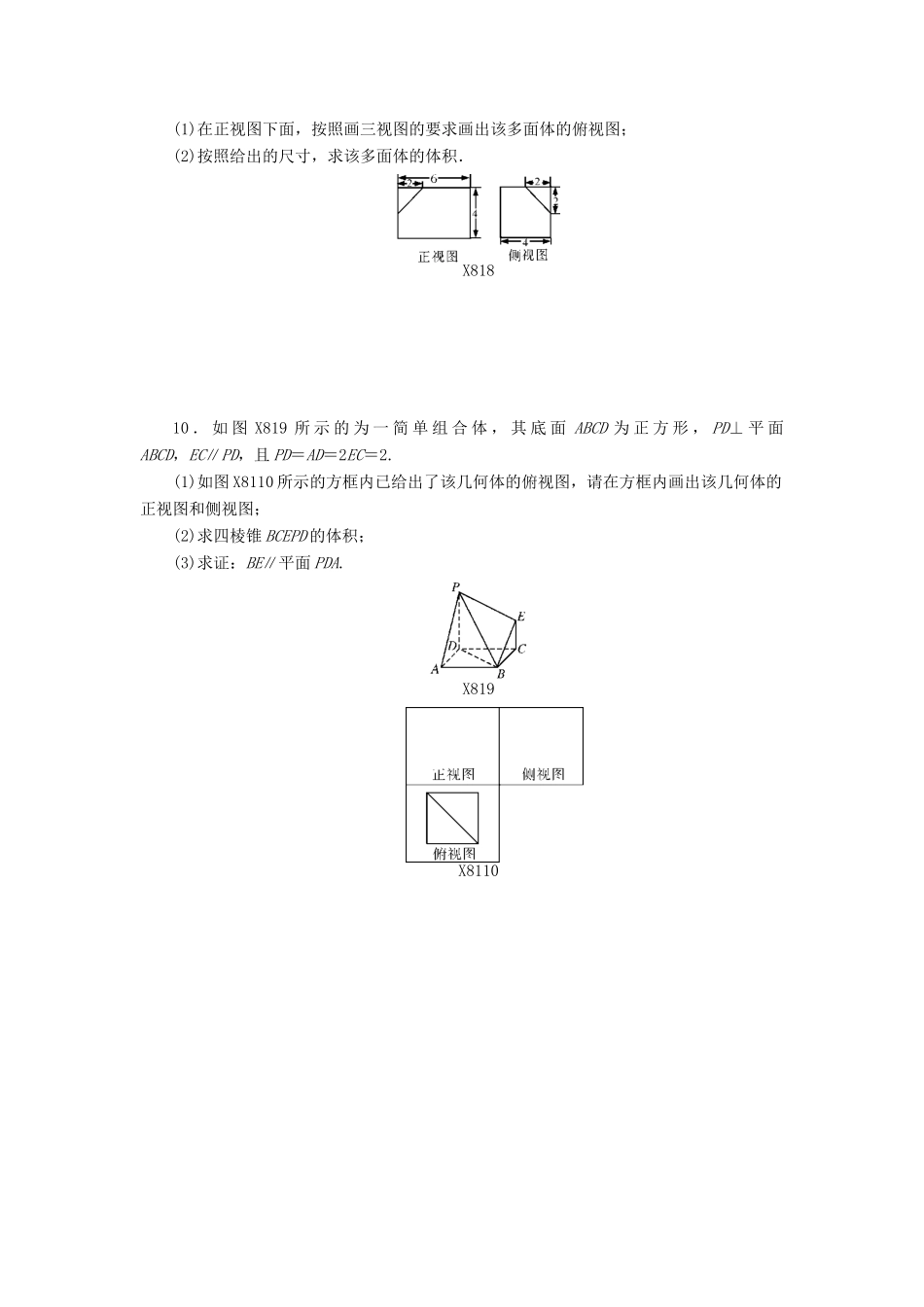
第八章立体几何第1讲空间几何体的三视图和直观图1.以下命题:①以直角三角形的一边为轴旋转一周所得的旋转体是圆锥;②以直角梯形的一腰为轴旋转一周所得的旋转体是圆台;③圆柱、圆锥、圆台的底面都是圆;④一个平面截圆锥,得到一个圆锥和一个圆台.其中正确命题的个数为()A.0个B.1个C.2个D.3个2.(2013年四川)一个几何体的三视图如图X811,则该几何体可以是()图X811A.棱柱B.棱台C.圆柱D.圆台3.如图X812,正方形O′A′B′C′的边长为1cm,它是水平放置的一个平面图形的直观图,则原图形的周长为()图X812A.6cmB.8cmC.(2+4)cmD.(2+2)cm4.(2015年广东汕头一模)一个锥体的主视图和左视图如下图X813,下面选项中,不可能是该锥体的俯视图的是()图X813ABCD5.如图X814是长和宽分别相等的两个矩形.给定下列三个命题:①存在三棱柱,其正视图、俯视图如图X814;②存在四棱柱,其正视图、俯视图如图X814;③存在圆柱,其正视图、俯视图如图X814.其中真命题的个数是()图X814A.3个B.2个C.1个D.0个6.已知某一几何体的正视图与侧视图如图X815,则在下列图形中,可以是该几何体的俯视图的图形为()图X815A.①②③⑤B.②③④⑤C.①②④⑤D.①②③④7.(2013年新课标Ⅱ)一个四面体的顶点在空间直角坐标系Oxyz中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以xOz平面为投影面,则得到的正视图可以为()ABCD8.如图X816,直三棱柱的正视图面积为2a2,则侧视图的面积为________.图X8169.如图X817所示的是一个长方体截去一个角所得多面体的直观图,它的正视图和侧视图在图X818中画出.X817(1)在正视图下面,按照画三视图的要求画出该多面体的俯视图;(2)按照给出的尺寸,求该多面体的体积.X81810.如图X819所示的为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC=2.(1)如图X8110所示的方框内已给出了该几何体的俯视图,请在方框内画出该几何体的正视图和侧视图;(2)求四棱锥BCEPD的体积;(3)求证:BE∥平面PDA.X819X8110第2讲空间几何体的表面积和体积1.(2014年福建)以边长为1的正方形的一边所在的直线为旋转轴,将该正方形旋转一周所得圆柱的侧面积等于()A.2πB.πC.2D.12.(2013年上海)若两个球的表面积之比为1∶4,则这两个球的体积之比为()A.1∶2B.1∶4C.1∶8D.1∶163.(2013年广东)某四棱台的三视图如图X821,则该四棱台的体积是()图X821A.4B.C.D.64.(2014年新课标Ⅱ)如图X822,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3cm,高为6cm的圆柱体毛坯切削得到,则切削的部分的体积与原来毛坯体积的比值为()A.B.C.D.图X822图X8235.圆柱形容器内盛有高度为8cm的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图X823),则球的半径是________cm.6.(2014年江苏)设甲、乙两个圆柱的底面面积分别为S1,S2,体积分别为V1,V2.若它们的侧面面积相等,且=,则=________.7.若一个圆锥的侧面展开图是面积为2π的半圆面,则该圆锥的体积为________.8.(2013年江苏)如图X824,在三棱柱A1B1C1ABC中,D,E,F分别是AB,AC,AA1的中点,设三棱锥FADE的体积为V1,三棱柱A1B1C1ABC的体积为V2,则V1∶V2=__________.图X8249.如图X825,设计一个正四棱锥形的冷水塔,高是1m,底面的边长是2m.(1)求这个正四棱锥形冷水塔的容积;(2)制造这个水塔的侧面需要的钢板的面积是多少?图X82510.如图X826,在三棱柱ABCA1B1C1中,侧棱垂直于底面,∠ACB=90°,AC=BC=AA1,D是棱AA1的中点.(1)证明:平面BDC1⊥平面BDC;(2)平面BDC1分此棱柱为两部分,求这两部分体积的比.图X826第3讲点、直线、平面之间的位置关系1.(2013年安徽)在下列命题中,不是公理的是()A.平行于同一个平面的两个平面相互平行B.过不在同一条直线上的三点,有且只有一个平面C.如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在此平面内D.如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线2.下列命题正...