高考数学试题分类汇编——立体几何VIP免费

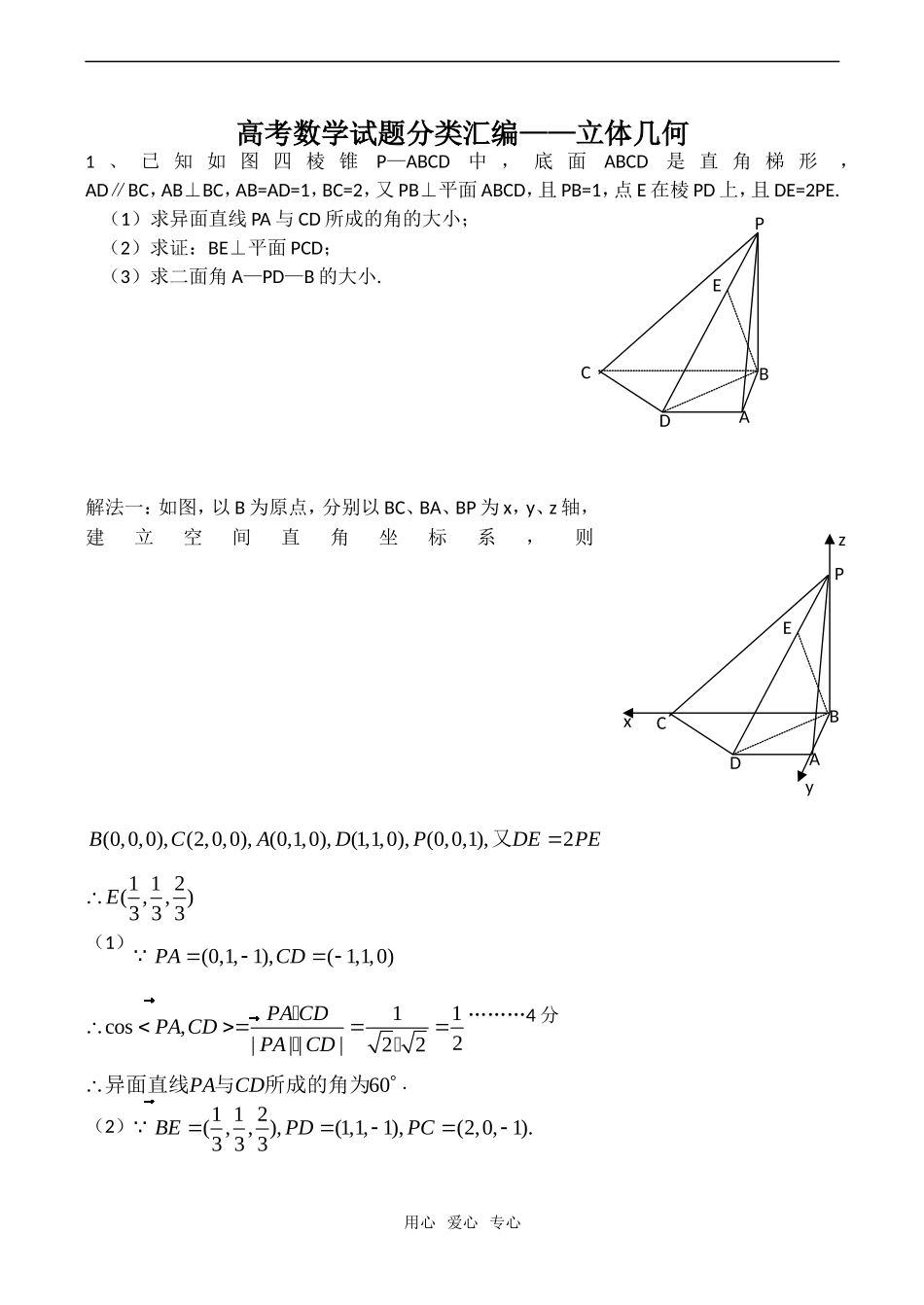
ABCDEPzxy高考数学试题分类汇编——立体几何1、已知如图四棱锥P—ABCD中，底面ABCD是直角梯形，AD∥BC，AB⊥BC，AB=AD=1，BC=2，又PB⊥平面ABCD，且PB=1，点E在棱PD上，且DE=2PE.（1）求异面直线PA与CD所成的角的大小；（2）求证：BE⊥平面PCD；（3）求二面角A—PD—B的大小.w.w.w.k.s.5.u.c.o.m解法一：如图，以B为原点，分别以BC、BA、BP为x，y、z轴，建立空间直角坐标系，则(0,0,0),(2,0,0),(0,1,0),(1,1,0),(0,0,1),2BCADPDEPE又112(,,)333E（1）(0,1,1),(1,1,0)PACD�11cos,2||||22PACDPACDPACD���………4分60PACD异面直线与所成的角为.（2）112(,,),(1,1,1),(2,0,1).333BEPDPC�用心爱心专心ABCDEP11211(1)0.333BEPD�11220(1)0.333BEPC�,,BEPDBEPCPDPCP又..ABPCD平面（3）设平面PAD的一个法向量为00000(,,),00nPAyznxyzxyznPD����则由得.令01,(2,1,1).zn则(0,0,1)BP�又，设平面PBD的法向量为1111(,,),nxyz1111110000znBPxyznPD����则由得令111,(1,1,0)xn则010101211(1)3cos,2||||62nnnnnn01,120nn又二面角A—PD—B为锐二面角，故二面角A—PD—B的大小为60.解法二：（1）取BC中点F，连结AF，则CF=AD，且CF∥AD，∴四边形ADCF是平行四边形，∴AF∥CD.∴∠PAF（或其补角）为异面直线PA与CD所成的角. PB⊥平面ABCD,∴PB⊥BA，PB⊥BF. PB=AB=BF=1，,ABBC∴PA=PF=AF=2.,60PAFPAF是正三角形即异面直线PA与CD所成的角等于60.（2）,1,2RtPBDPBBD在中,PD=3用心爱心专心ABCDEPHFO32,3DEPEPE，则13PEPBPBPD.~PBEPDBBEPD.由（1）知，,90CFBFDFCDB..,,.CDBDBCDPBCD又PB平面,,,PBBDBCDPBDCDBE平面,.CDPDDBEPCD平面（3）设AF与BD的交点为O，则AOBD.,.PBPBDABDAOPBD平面ABCD,平面平面平面过点O作OHPD于点H，连结AH，则AHPD.AHOAPDB为二面角的平面角。在2,2RtABDAO中.在216,33PAADRtPADAHPD中.在232,sin263AORtAOHAHOAH中.60,AHOAPDB即二面角的大小为60.2、如图(1)在直角梯形ABCP中，BC∥AP，AB⊥BC，CD⊥AP，AD＝DC＝PD＝2，E、F、G分别是PC、PD、BC的中点，现将△PDC沿CD折起，使平面PDC⊥平面ABCD(如图2)(1)求二面角G－EF－D的大小；(2)(理科)在线段PB上确定一点Q，使PC⊥平面ADQ，并给出证明过程.用心爱心专心(文科)当Q点落在PB中点时，求PC与平面ADQ所成角的大小.(1)∠DFH就是二面角G－EF－D的平面角…2分在Rt△HDF中，DF＝PD＝1，DH＝AD＝1…………4分∴∠DFH＝45°，即二面角G－EF－D的大小为45°.…………6分(2)当点Q是线段PB的中点时，有PQ⊥平面ADQ.…………7分证明如下：E是PC中点，∴EQ∥BC，又AD∥BC，故EQ∥AD，从而A、D、E、Q四点共面在Rt△PDC中，PD＝DC，E为PC中点∴PC⊥DE，又 PD⊥平面ABCD…………10分∴AD⊥PC，又AD∩DE＝D∴PC⊥平面ADEQ，即PC⊥平面ADQ.…………12分解法二：(1)建立如图所示空间直角坐标系，设平面GEF的一个法向量为n＝(x，y，z)，则取n＝(1，0，1)…………4分又平面EFD的法向量为m＝(1，0，0)∴cos＝…………6分∴＝45°…………7分(2)设PQ＝λPB(0＜λ＜1)则AQ＝AP＋PQ＝(－2＋2λ，2λ，2－2λ)…………9分AQ⊥PCAQ·PC＝02×2λ－2(2－2λ)＝0λ＝…………11分又AD⊥PC，∴PC⊥平面ADQλ＝点Q是线段PB的中点.…………12分(注：文科试题请参考上面解答相应给分)3．如图，直四棱柱ABCD—A1B1C1D1的高为3，底面是边长为4且∠DAB=60°的菱形，AC∩BD=O，A1C1∩B1D1=O1，E是O1A的中点.（1）求二面角O1－BC－D的大小；（2）求点E到平面O1BC的距离.解法一（1）过O作OFBC⊥于F，连接O1F，用心爱心专心EO1OD1C1B1DCBAA1OO1⊥面AC，∴BCO⊥1F，O∴∠1FO是二面角O...