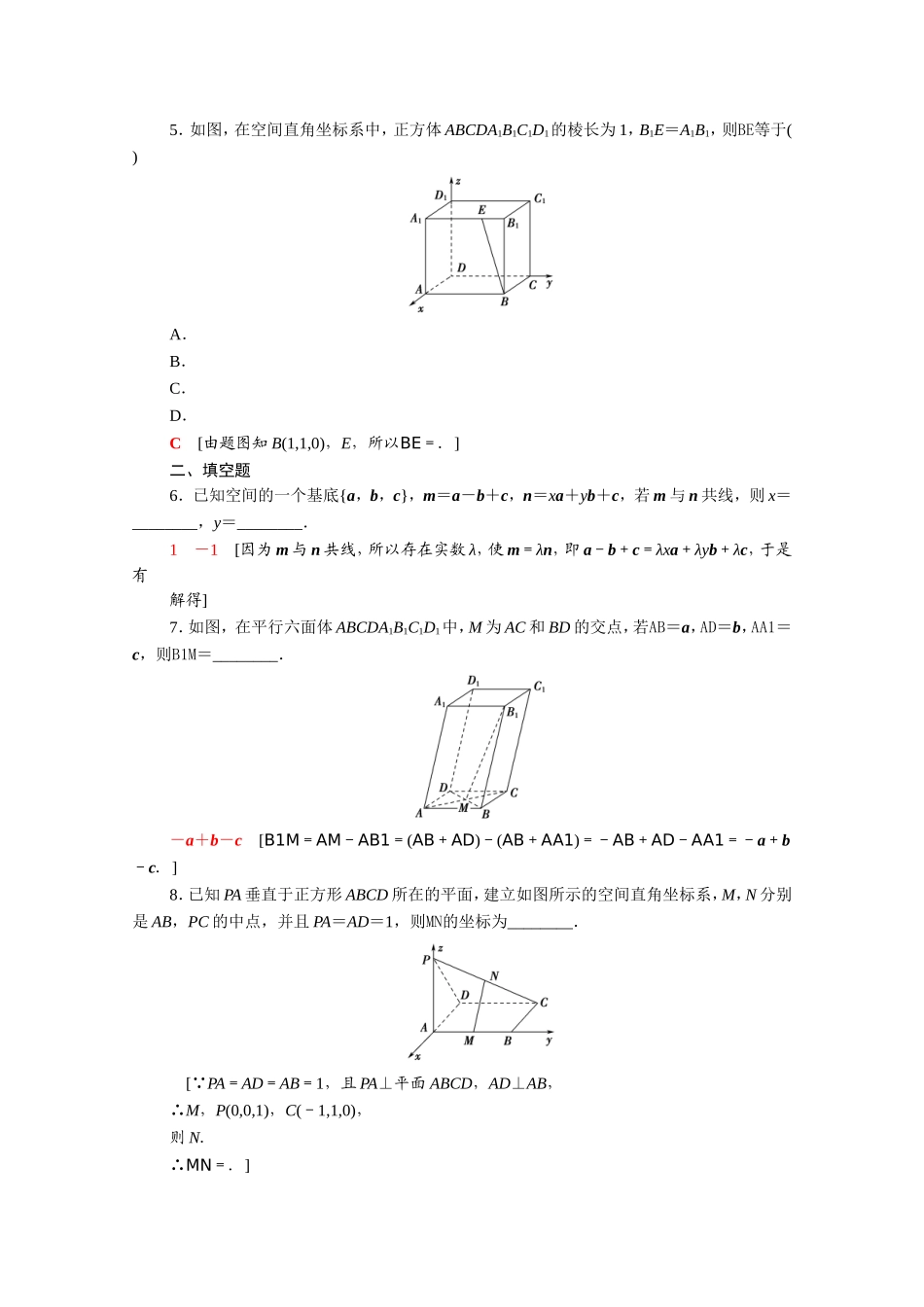
课时分层作业(十六)空间向量的正交分解及其坐标表示(建议用时:60分钟)一、选择题1.给出下列命题:①若{a,b,c}可以作为空间的一个基底,d与c共线,d≠0,则{a,b,d}也可以作为空间的一个基底;②已知向量a∥b,则a,b与任何向量都不能构成空间的一个基底;③A,B,M,N是空间四点,若BA,BM,BN不能构成空间的一个基底,则A,B,M,N四点共面;④已知{a,b,c}是空间的一个基底,若m=a+c,则{a,b,m}也是空间的一个基底.其中正确命题的个数是()A.1B.2C.3D.4D[根据基底的概念,知空间中任何三个不共面的向量都可作为空间的一个基底.显然②正确.③中由BA,BM,BN不能构成空间的一个基底,知BA,BM,BN共面.又BA,BM,BN过相同点B,知A,B,M,N四点共面.所以③正确.下面证明①④正确:①假设d与a,b共面,则存在实数λ,μ,使得d=λa+μb, d与c共线,c≠0,∴存在实数k,使得d=kc. d≠0,∴k≠0,从而c=a+b,∴c与a,b共面,与条件矛盾,∴d与a,b不共面.同理可证④也是正确的.于是①②③④四个命题都正确,故选D.]2.已知i,j,k是空间直角坐标系Oxyz中x轴、y轴、z轴正方向上的单位向量,且AB=-i+j-k,则B点的坐标为()A.(-1,1,-1)B.(-i,j,-k)C.(1,-1,-1)D.不确定D[AB=-i+j-k,只能确定AB的坐标为(-1,1,-1),而A点坐标不确定,所以B点坐标也不确定.]3.正方体ABCDA′B′C′D′中,O1,O2,O3分别是AC,AB′,AD′的中点,以{AO1,AO2,AO3}为基底,AC′=xAO1+yAO2+zAO3,则x,y,z的值是()A.x=y=z=1B.x=y=z=C.x=y=z=D.x=y=z=2A[AC′=AA′+AD+AB=(AB+AD)+(AA′+AD)+(AA′+AB)=AC+AD′+AB′=AO1+AO3+AO2,由空间向量的基本定理,得x=y=z=1.]4.已知点O,A,B,C为空间不共面的四点,且向量a=OA+OB+OC,向量b=OA+OB-OC,则与a,b不能构成空间基底的向量是()A.OAB.OBC.OCD.OA或OBC[因为a-b=2OC,所以a,b与OC共面,不能构成空间的一个基底.]5.如图,在空间直角坐标系中,正方体ABCDA1B1C1D1的棱长为1,B1E=A1B1,则BE等于()A.B.C.D.C[由题图知B(1,1,0),E,所以BE=.]二、填空题6.已知空间的一个基底{a,b,c},m=a-b+c,n=xa+yb+c,若m与n共线,则x=________,y=________.1-1[因为m与n共线,所以存在实数λ,使m=λn,即a-b+c=λxa+λyb+λc,于是有解得]7.如图,在平行六面体ABCDA1B1C1D1中,M为AC和BD的交点,若AB=a,AD=b,AA1=c,则B1M=________.-a+b-c[B1M=AM-AB1=(AB+AD)-(AB+AA1)=-AB+AD-AA1=-a+b-c.]8.已知PA垂直于正方形ABCD所在的平面,建立如图所示的空间直角坐标系,M,N分别是AB,PC的中点,并且PA=AD=1,则MN的坐标为________.[ PA=AD=AB=1,且PA⊥平面ABCD,AD⊥AB,∴M,P(0,0,1),C(-1,1,0),则N.∴MN=.]三、解答题9.如图所示,正方体OABCO′A′B′C′,且OA=a,OC=b,OO′=c.(1)用a,b,c表示向量OB′,AC′;(2)设G,H分别是侧面BB′C′C和O′A′B′C′的中心,用a,b,c表示GH.[解](1)OB′=OB+BB′=OA+OC+OO′=a+b+c.AC′=AC+CC′=AB+AO+AA′=OC+OO′-OA=b+c-a.(2)GH=GO+OH=-OG+OH=-(OB′+OC)+(OB′+OO′)=OO′-OC=(c-b).10.在平行六面体ABCDA1B1C1D1中,设AB=a,AD=b,AA1=c,E,F分别是AD1,BD的中点.(1)用向量a,b,c表示D1B,EF;(2)若D1F=xa+yb+zc,求实数x,y,z的值.[解](1)如图,D1B=D1D+DB=-AA1+AB-AD=a-b-c,EF=EA+AF=D1A+AC=-(AA1+AD)+(AB+AD)=(a-c).(2)D1F=(D1D+D1B)=(-AA1+D1B)=(-c+a-b-c)=a-b-c,∴x=,y=-,z=-1.1.已知空间四边形OABC,其对角线为AC,OB,M,N分别是OA,BC的中点,点G是MN的中点,则OG等于()A.OA+OB+OCB.(OA+OB+OC)C.D.OB+OA+OCB[如图,OG=(OM+ON)=OM+×(OB+OC)=OA+OB+OC=(OA+OB+OC).]2.已知在长方体ABCDA1B1C1D1中,向量a在基底{AB,AD,AA1}下的坐标为(2,1,-3),则向量a在基底{DA,DC,DD1}下的坐标为()A.(2,1,-3)B.(-...