高二数学抛物线人教版知识精点VIP免费

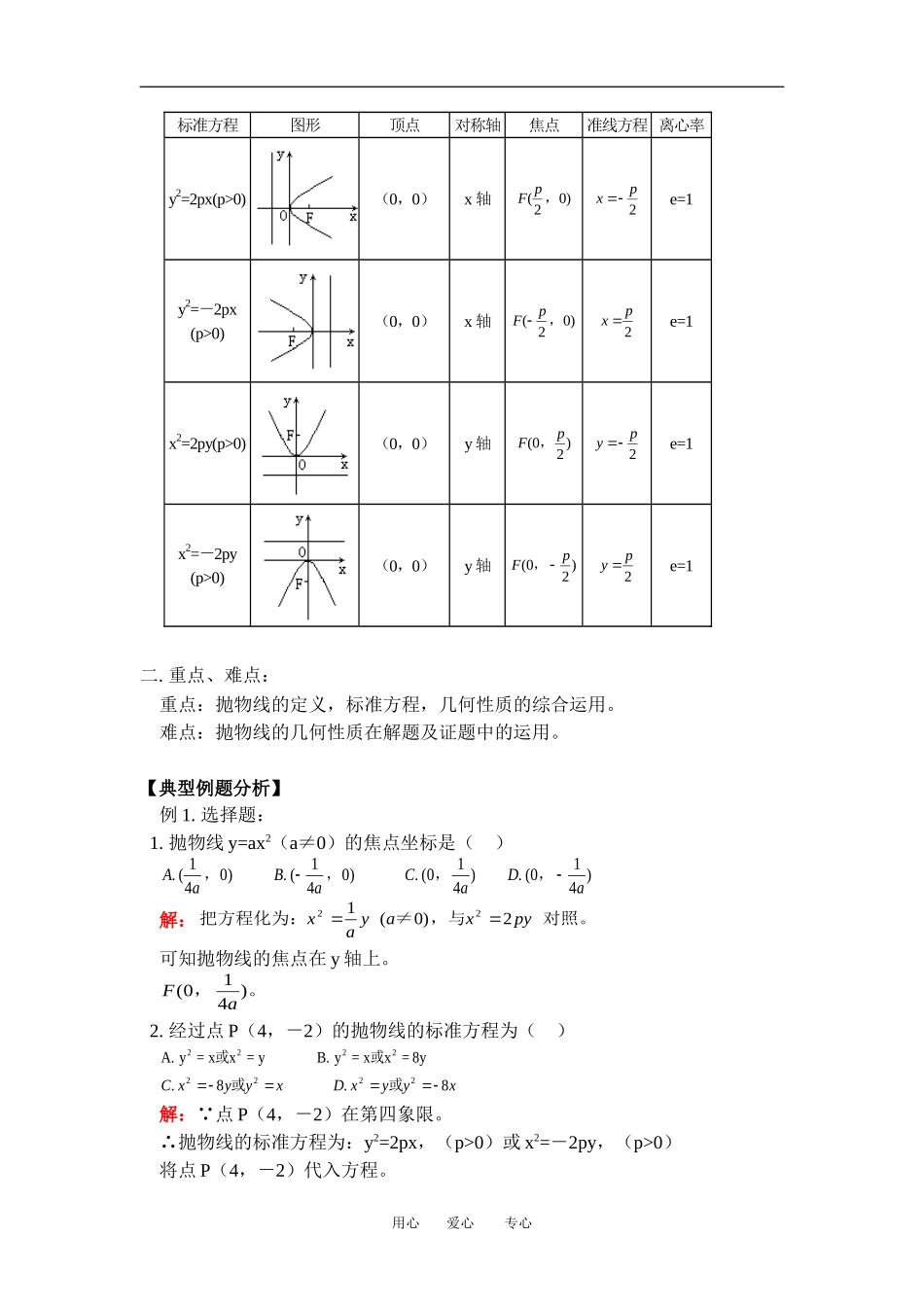
高二数学抛物线人教版【同步教育信息】一.本周教学内容：《抛物线》教学目标：1.理解并掌握抛物线的定义及其标准方程。2.理解并掌握抛物线的性质，并会画图。3.掌握抛物线单元中的相关知识，并会综合应用。能力训练：1.掌握抛物线的定义及标准方程、几何性质的综合应用。2.会求轨迹方程及抛物线的实际应用问题。3.准确把握抛物线标准方程的四种形式，进一步巩固待定系数法。4.进一步培养学生数形结合的能力，并能灵活运用常用的一些数学变换方法解决综合性问题。教学过程：知识提要：1.抛物线的定义：平面内与一个定点F和一条定直线l的距离相等的点的轨迹叫做抛物线，定点F叫抛物线的焦点，直线l叫抛物线的准线。2.抛物线的标准方程：（1）顶点在原点，焦点在x轴正半轴上：y2=2px，（p>0）。（2）顶点在原点，焦点在x轴负半轴上：y2=－2px，（p>0）。（3）顶点在原点，焦点在y轴的正半轴上：x2=2py，（p>0）。（4）顶点在原点，焦点在y轴负半轴上，x2=－2py，（p>0）。3.抛物线的几何性质：（1）焦点在x轴正半轴上的抛物线y2=2px，（p>0）的几何性质：①范围：x≥0，y∈R。②对称性：图形关于x轴对称。③顶点：0（0，0）。④离心率：e=1。⑤准线：。xp2说明：其实从图形上就可以反映前三条性质，下面列表给出四种形式的性质：用心爱心专心标准方程图形顶点对称轴焦点准线方程离心率y2=2px(p>0)（0，0）x轴Fp()20，xp2e=1y2=－2px(p>0)（0，0）x轴Fp()20，xp2e=1x2=2py(p>0)（0，0）y轴Fp()02，yp2e=1x2=－2py(p>0)（0，0）y轴Fp()02，yp2e=1二.重点、难点：重点：抛物线的定义，标准方程，几何性质的综合运用。难点：抛物线的几何性质在解题及证题中的运用。【典型例题分析】例1.选择题：1.抛物线y=ax2（a≠0）的焦点坐标是（）AaBaCaDa.().().().()140140014014，，，，解：把方程化为：≠，与对照。xayaxpy22102()可知抛物线的焦点在y轴上。Fa()014，。2.经过点P（4，－2）的抛物线的标准方程为（）A.y=xx=yB.y=xx=8y2222或或CxyyxDxyyx..222288或或解： 点P（4，－2）在第四象限。∴抛物线的标准方程为：y2=2px，（p>0）或x2=－2py，（p>0）将点P（4，－2）代入方程。用心爱心专心（－2）2=8p1或42=4p2∴或pp12124∴所求抛物线的标准方程为：y2=x或x2=－8y∴选C。3.过抛物线y2=4x的焦点作直线交抛物线于A（x1，y1）、B（x2，y2），如果x1+x2=6，则|AB|的值为（）A.10B.8C.6D.4解： y2=4x∴2p=4，p=2。∴由抛物线定义知：|AF|=x1+1，|BF|=x2+1∴|AB|=|AF|+|BF|=x1+x2+2=6+2=8∴选B。4.过已知点A（0，p）且与抛物线y2=2px(p>0)只有一个公共点的直线会有（）A.1条B.2条C.3条D.无数条解：①当直线的斜率不存在时，则过点A（0，p）的直线恰为y轴，此时抛物线与直线只有一个公共点。②当过A（0，p）的直线斜率存在时，设方程为y=kx+p由方程组消去：ykxbypxykxpkpxp22222220()若得，此时直线过，且与轴平行kxpApx020()直线与抛物线只有一个公共点，坐标为，。()pp2若≠，。kpkpkk0214012222[()]则直线与抛物线只有一个公共点。yxp12∴选C。例2.直线l：y=kx+1，抛物线C：y2=4x，当k为何值时，l与C相切、相交、相离。解：将与的方程联立，①②lCykxyx142①代入②整理得：。kxkx222410()当≠时，是一元二次方程，∴kkkk024416122()（1）当Δ=0时，即k=1时，l与C相切。（2）当Δ>0时，即k<1时，l与C相交。（3）当Δ<0时，即k>1时，l与C相离。用心爱心专心当k=0时，l：y=1与y2=4x相交。注：直线与抛物线有一个公共点是直线与抛物线相切的必要但不充分条件。例3.顶点在原点，焦点在y轴上的抛物线被直线x－2y－1=0截得的弦长为15，求这抛物线方程。解：依题意设抛物线方程为：x2=ay（a≠0），xayxyyxaxa22120消去得 直线与抛物线有两个交点。∴×∴或。()aaaa242008设直线与抛物线的两个交点坐标为A（x1，y1），B（x2，y2）则，·，xxaxxayyxx121212122212()∴||()()()ABxxyyxx12212212254...