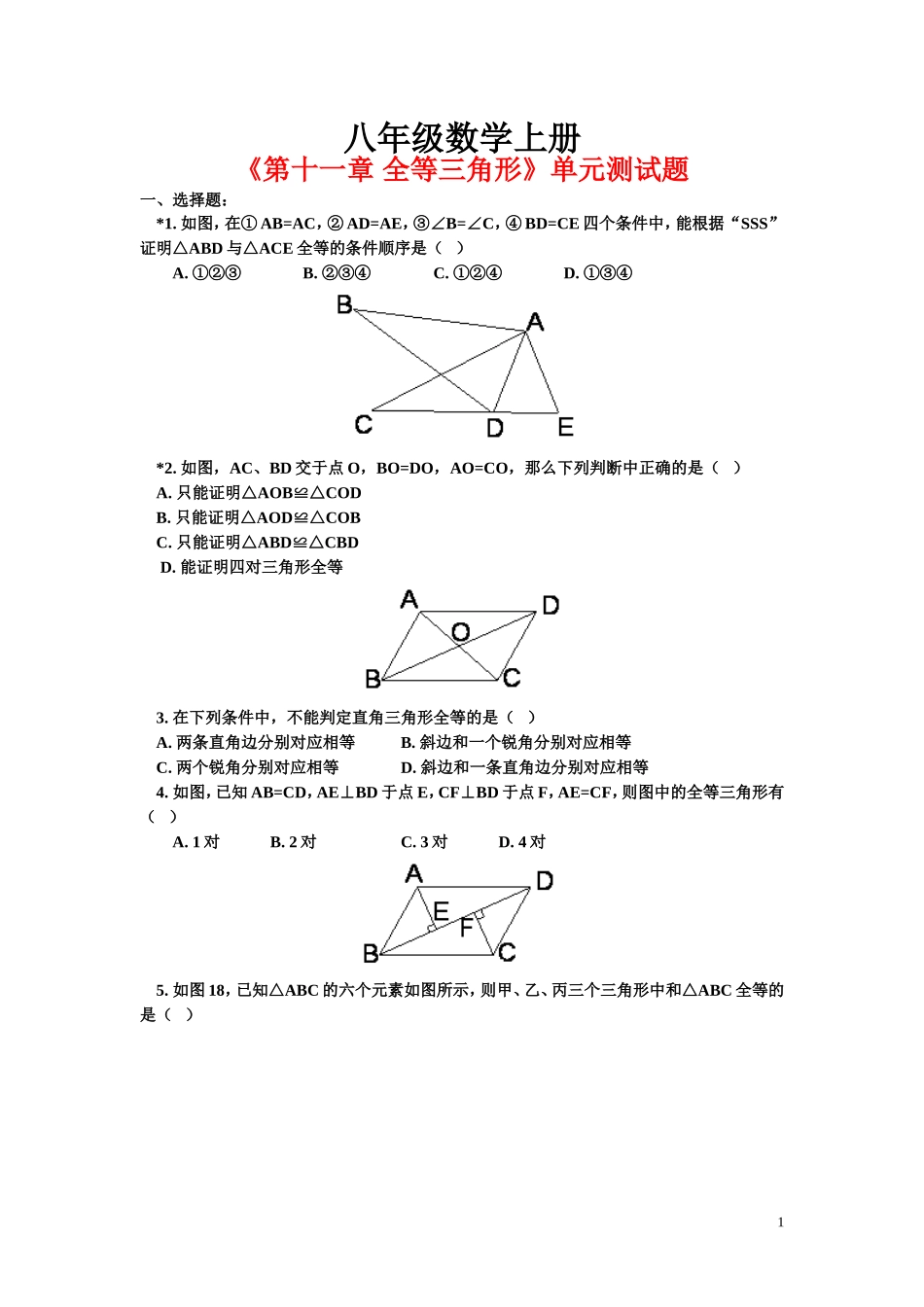
八年级数学上册《第十一章全等三角形》单元测试题一、选择题:*1.如图,在①AB=AC,②AD=AE,③∠B=∠C,④BD=CE四个条件中,能根据“SSS”证明△ABD与△ACE全等的条件顺序是()A.①②③B.②③④C.①②④D.①③④*2.如图,AC、BD交于点O,BO=DO,AO=CO,那么下列判断中正确的是()A.只能证明△AOB≌△CODB.只能证明△AOD≌△COBC.只能证明△ABD≌△CBDD.能证明四对三角形全等3.在下列条件中,不能判定直角三角形全等的是()A.两条直角边分别对应相等B.斜边和一个锐角分别对应相等C.两个锐角分别对应相等D.斜边和一条直角边分别对应相等4.如图,已知AB=CD,AE⊥BD于点E,CF⊥BD于点F,AE=CF,则图中的全等三角形有()A.1对B.2对C.3对D.4对5.如图18,已知△ABC的六个元素如图所示,则甲、乙、丙三个三角形中和△ABC全等的是()1A.甲、乙B.乙、丙C.只有乙D.只有丙二、填空题:6.如图,AB=AC,BE=CD,要使△ABE≌△ACD,依据“SSS”,则还需添加条件:。**7.如图,AD和A’D’分别是锐角△ABC和锐角△A’B’C’中BC和B’C’边上的高,且BC=B’C’,AD=A’D’,若使△ABC≌△A’B’C’,请你补充条件。(填一个你认为适当的条件)**8.如图,△ABC是不等边三角形,DE=BC,以D、E为两个顶点作位置不同的三角形,使所作的三角形与△ABC全等,这样的三角形最多可以画出_____个。2三、解答题:9.已知:如图,OP是AOC和BOD的平分线,OAOCOBOD,。求证:(1)△OAB≌△OCD;(2)ABCD。**10.如图,在△AFD和△CEB中,点A,E,F,C在同一直线上,有下面四个论断:(1)AD=CB;(2)AE=CF;(3)∠B=∠D;(4)AD∥BC。请将其中三个论断作为条件,余下的一个作为结论,编一道证明题,并写出证明过程。3一、选择题:1.C2.D3.C4.C5.B二、填空题:6.AD=AE;7.∠B=∠B';8.4三、解答题:9.证明:(1) OP平分∠AOC和∠BOD∴∠AOP=∠COP,∠BOP=∠DOP∴∠AOP-∠BOP=∠COP-∠DOP∴∠AOB=∠COD在△AOB和△COD中, ODOBCODAOBOCOA∴△AOB≌△COD(SAS)(2)由(1)得△AOB≌△COD(SAS)∴AB=CD10.已知,如图,在△AFD和△CEB中,点A,E,F,C在同一直线上,且AD=CB,AE=CF,AD∥BC。求证:∠B=∠D。证明: AD∥BC∴∠A=∠C AE=CF∴AE+EF=CF+EF∴AF=CE在△ADF和△CBE中, CEAFCACBAD∴△ADF≌△CBE(SAS)∴∠B=∠D4《第十二章轴对称》单元测试题一选择题:(每小题3分,共24分)1、下列说法正确的是()A轴对称涉及两个图形,轴对称图形涉及一个图形B如果两条线段互相垂直平分,那么这两条线段互为对称轴C所有直角三角形都不是轴对称图形D有两个内角相等的三角形不是轴对称图形2、若等腰三角形的一边长为10,另一边长为7,则它的周长为()A17B24C27D24或273、若一个三角形的三个外角的度数之比为5∶4∶5,则这个三角形是()A等腰三角形,但不是等边三角形,也不是等腰直角三角形B直角三角形,但不是等腰三角形C等腰直角三角形D等边三角形4、等腰三角形底边长为5cm,一腰上的中线分其周长的两部分的差为3cm,则腰长为()A2cmB8cmC2cm或8cmD以上答案都不对5、下列说法正确的个数有()⑴等边三角形有三条对称轴⑵四边形有四条对称轴⑶等腰三角形的一边长为4,另一边长为9,则它的周长为17或22⑷一个三角形中至少有两个锐角A1个B2个C3个D4个6、若一个三角形一条边上的中点到其他两边的距离相等,那么这个三角形一定是()A等边三角形B等腰三角形C不等边三角形D不确定在平面直角坐标系中,直线y=2x-3关于x轴对称的直线是()Ay=2x+3By=-2x+3Cy=-2x-3Dy=-3x+27、如图,∠BAC=90o,AD⊥BC,DE⊥AC,DF⊥AB,AC=BC,除图中AC和BC外,关系形如a=b的线段对还有()A2对B4对C6对D7对8.(2008台州市).把一个图形先沿着一条直线进行轴对称变换,再沿着与这条直线平行的方向平移,我们把这样的图形变换叫做滑动对称变换.在自然界和日常生活中,大量地存在这种图形变换(如图1).结合轴对称变换和平移变换的有关性质,你认为在滑动对称变换过程中,两个对应三角形(如图2)的对应点所具有的性质是()A.对应点连线与对称轴垂直B.对应点连线被对称轴...