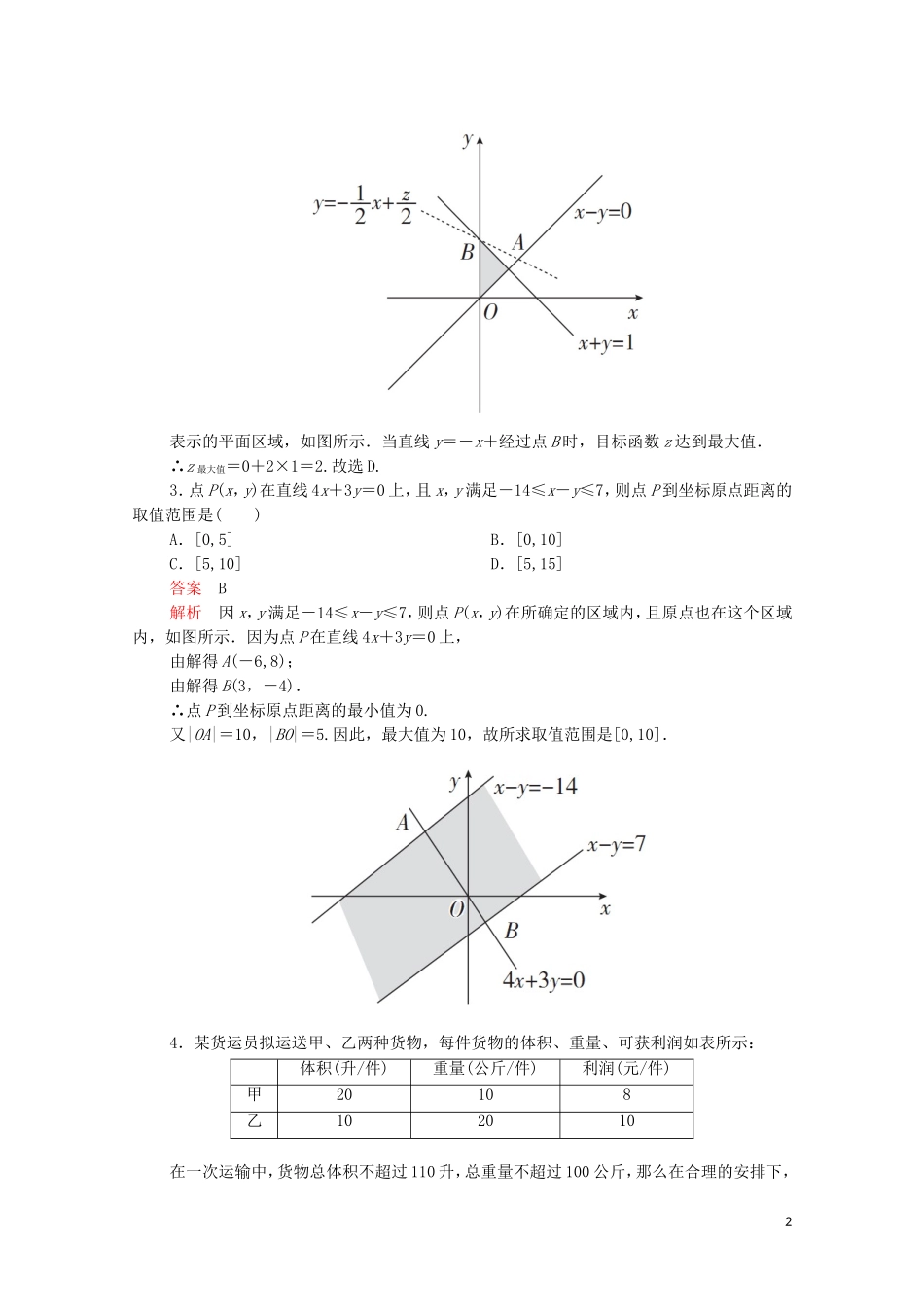
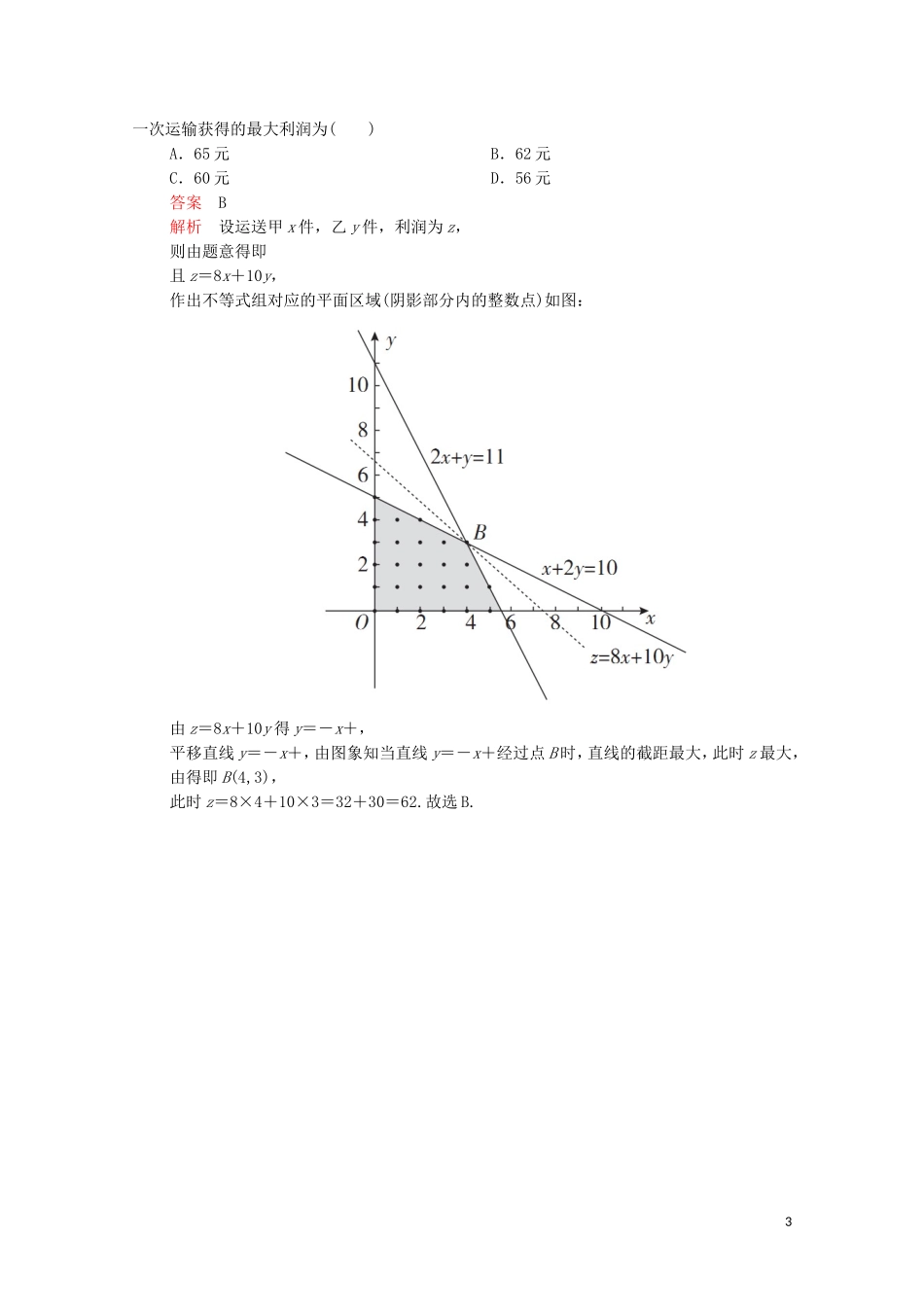
3.3.2简单的线性规划问题A级:基础巩固练一、选择题1.已知P(x,y)为区域内的任意一点,当该区域的面积为4时,z=2x-y的最大值是()A.6B.0C.2D.2答案A解析画出不等式组所表示的平面区域如图所示,由图可知A(a,-a),B(a,a),由S△AOB=×2a×a=4,得a=2.所以A(2,-2),由z=2x-y化简得y=2x-z,即当y=2x-z过A点时z取最大值,且zmax=2×2-(-2)=6.故选A.2.若x,y满足则z=x+2y的最大值为()A.0B.1C.D.2答案D解析作出不等式组1表示的平面区域,如图所示.当直线y=-x+经过点B时,目标函数z达到最大值.∴z最大值=0+2×1=2.故选D.3.点P(x,y)在直线4x+3y=0上,且x,y满足-14≤x-y≤7,则点P到坐标原点距离的取值范围是()A.[0,5]B.[0,10]C.[5,10]D.[5,15]答案B解析因x,y满足-14≤x-y≤7,则点P(x,y)在所确定的区域内,且原点也在这个区域内,如图所示.因为点P在直线4x+3y=0上,由解得A(-6,8);由解得B(3,-4).∴点P到坐标原点距离的最小值为0.又|OA|=10,|BO|=5.因此,最大值为10,故所求取值范围是[0,10].4.某货运员拟运送甲、乙两种货物,每件货物的体积、重量、可获利润如表所示:体积(升/件)重量(公斤/件)利润(元/件)甲20108乙102010在一次运输中,货物总体积不超过110升,总重量不超过100公斤,那么在合理的安排下,2一次运输获得的最大利润为()A.65元B.62元C.60元D.56元答案B解析设运送甲x件,乙y件,利润为z,则由题意得即且z=8x+10y,作出不等式组对应的平面区域(阴影部分内的整数点)如图:由z=8x+10y得y=-x+,平移直线y=-x+,由图象知当直线y=-x+经过点B时,直线的截距最大,此时z最大,由得即B(4,3),此时z=8×4+10×3=32+30=62.故选B.3二、填空题5.已知O为坐标原点,点M(3,2),若点N(x,y)满足不等式组则OM·ON的最大值为________.答案12解析画出所给不等式组表示的平面区域如图所示.令z=OM·ON=3x+2y,由目标函数的几何意义可知当z=3x+2y过(4,0)点时,z取最大值,即OM·ON的最大值=3×4+0=12.6.若已知实数x,y满足不等式组则z=|x+2y-4|的最大值是________.答案21解析作出不等式组表示的平面区域,如图中阴影部分所示.解法一:z=|x+2y-4|=×,其几何意义为阴影区域内的点到直线x+2y-4=0的距离的倍.由得点B的坐标为(7,9),显然点B到直线x+2y-4=0的距离最大,此时zmax=21.解法二:由图可知,阴影区域(可行域)内的点都在直线x+2y-4=0的上方,显然此时有4x+2y-4>0,于是目标函数等价于z=x+2y-4,即转化为一般的线性规划问题.显然当直线经过点B时,目标函数z取得最大值,由得点B的坐标为(7,9),此时zmax=21.7.不等式组所确定的平面区域记为D.若点(x,y)是区域D上的点,则2x+y的最大值是________;若圆O:x2+y2=r2上的所有点都在区域D内,则圆O面积的最大值是________.答案14解析作出区域D如图所示.令z=2x+y可知,直线z=2x+y经过点(4,6)时z最大,此时z=14;当圆O:x2+y2=r2和直线2x-y-2=0相切时半径最大,此时半径r=,面积S=.三、解答题8.已知实数x,y满足试求z=的最大值和最小值.解由于z==,所以z的几何意义是点(x,y)与点M(-1,-1)连线的斜率,因此,的最值就是点(x,y)与点M(-1,-1)连线的斜率的最值,作出表示的可行域如下图所示:5结合图可知,直线MB的斜率最大,直线MC的斜率最小,即zmax=kMB=3,此时x=0,y=2;zmin=kMC=,此时x=1,y=0.所以z的最大值为3,最小值为.9.一农民有农田2亩,根据往年经验,若种水稻,则每亩产量为400千克;若种花生,则每亩产量为100千克.但水稻成本较高,每亩240元,而花生只需80元,且花生每千克5元,稻米每千克3元.现该农民手头有400元.(1)设该农民种x亩水稻,y亩花生,利润z元,请写出约束条件及目标函数;(2)问两种作物各种多少,才能获得最大收益?解(1)约束条件为:即目标函数为:z=(3×400-240)x+(5×100-80)y=960x+420y.(2)作出可行域如图所示,6把z=960x+420y变形为y=-x+,得到斜率为-,在y轴上的截距为,随z变化的一组平行直线;当直线y=-x+经过可行域上的...