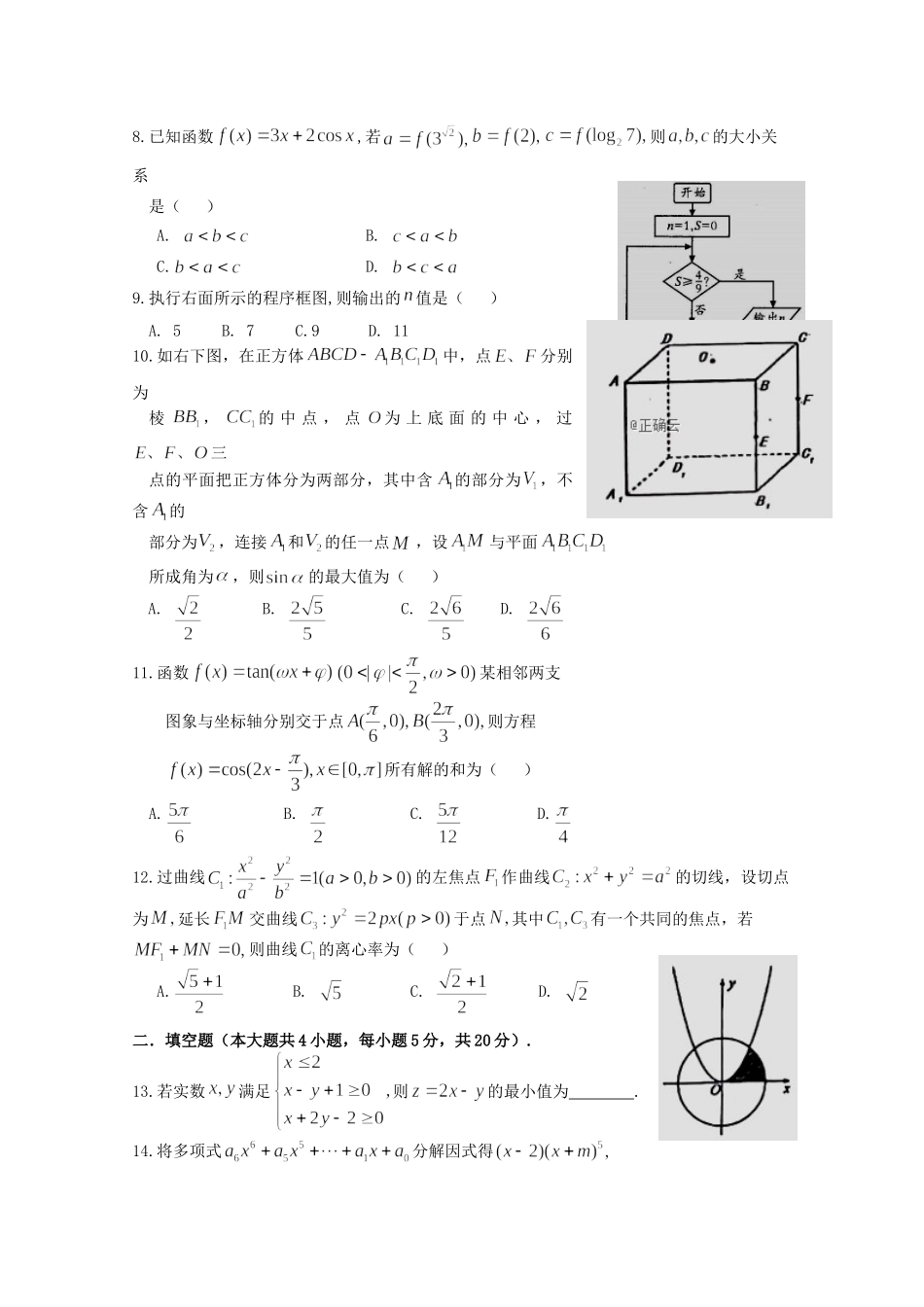
静乐一中2019学年第二学期高三年级第三次月考数学试题(理)一.选择题(本大题共12题,每小题5分,共60分.在每小题的四个选项中只有一个选项是正确的.)1.已知全集则()A.B.C.D.2.设复数满足(其中为虚数单位),则()A.B.C.D.3.某所学校在一个学期的开支分布的饼图如图1所示,在该学期的水、电、交通开支(单位:万元)如图2所示,则该学期的电费开支占总开支的百分比为()A.B.C.D.4.已知定义在上的奇函数满足:当时,则()A.B.C.3D.5.几何体的三视图如图所示,则这个几何体的直观图可以是()A.B.C.D.6.等差数列的前项和为,若则()A.152B.154C.156D.1587.在中,则在方向上的投影为()A.4B.3C.4D.58.已知函数,若则的大小关系是()A.B.C.D.9.执行右面所示的程序框图,则输出的值是()A.5B.7C.9D.1110.如右下图,在正方体中,点分别为棱,的中点,点为上底面的中心,过三点的平面把正方体分为两部分,其中含的部分为,不含的部分为,连接和的任一点,设与平面所成角为,则的最大值为()A.B.C.D.11.函数某相邻两支图象与坐标轴分别交于点则方程所有解的和为()A.B.C.D.12.过曲线的左焦点作曲线的切线,设切点为延长交曲线于点其中有一个共同的焦点,若则曲线的离心率为()A.B.C.D.二.填空题(本大题共4小题,每小题5分,共20分).13.若实数满足则的最小值为.14.将多项式分解因式得为常数,若,则.15.如右图所示,阴影部分是由曲线和圆及轴围成的封闭图形.在圆内随机取一点,则此点取自则阴影部分的概率为.16.设锐角三个内角所对的边分别为,若则的取值范围为.三.解答题(本大题共5小题,共70分.)17.(本小题满分12分)已知数列的前项和为,且满足.(1)求数列的通项公式;(2)令,为的前项和,求证:.18.(本小题满分12分)如图,在四棱锥中,,底面四边形为直角梯形,为线段上一点.(1)若,则在线段上是否存在点,使得平面?若存在,请确定点的位置;若不存在,请说明理由(2)己知,若异面直线与成角,二面角的余弦值为,求的长.19.(本小题满分12分)2019年2月13日《烟台市全民阅读促进条例》全文发布,旨在保障全民阅读权利,培养全民阅读习惯,提高全民阅读能力,推动文明城市和文化强市建设.某高校为了解条例发布以来全校学生的阅读情况,随机调查了200名学生每周阅读时间(单位:小时)并绘制如图所示的频率分布直方图.(1)求这200名学生每周阅读时间的样本平均数和样本方差(同一组中的数据用该组区间的中间值代表);(2)由直方图可以认为,目前该校学生每周的阅读时间服从正态分布,其中近似为样本平均数,近似为样本方差.(i)一般正态分布的概率都可以转化为标准正态分布的概率进行计算:若.利用直方图得到的正态分布,求.(ii)从该高校的学生中随机抽取20名,记表示这20名学生中每周阅读时间超过10小时的人数,求(结果精确到0.0001)以及的数学期望.参考数据:20.(本小题满分12分)已知点是动点,且直线和直线的斜率之积为.(1)求动点的轨迹方程;(2)设直线与(1)中轨迹相切于点,与直线相交于点且求证:21.(本小题满分12分)已知函数(1)当时,取得极值,求的值并判断是极大值点还是极小值点;(2)当函数有两个极值点且时,总有成立,求的取值范围.请考生在22~23题中任选一题作答,如果多选,则按所做的第一题记分.22.(本小题满分10分)在极坐标系中,曲线的方程为,点.(1)以极点为原点,极轴为轴的正半轴,建立平面直角坐标系,把曲线的极坐标方程化为直角坐标方程,点的极坐标化为直角坐标;(2)设为曲线上一动点,以为对角线的矩形的一边垂直于极轴,求矩形周长的最小值及此时点的直角坐标.23.(本小题满分10分)已知(1)当时,求不等式的解集;(2)若不等式的解集为实数集,求实数的取值范围.静乐一中2019学年第二学期高三年级第三次月考理数答案一.选择题(本大题共12题,每小题5分,共60分.在每小题的四个选项中只有一个选项是正确的.)CBBAB,CCDCB,AA二.填空题(本大题共4小题,每小题5分,共20分).13.114.215.16.三.解答题(本大题共5小题,共70分.)17.【解析】(1)当时,可得-----------2分即得又因为,代入可得满足上式,所以数列是首项为2,公比为4的等比数...