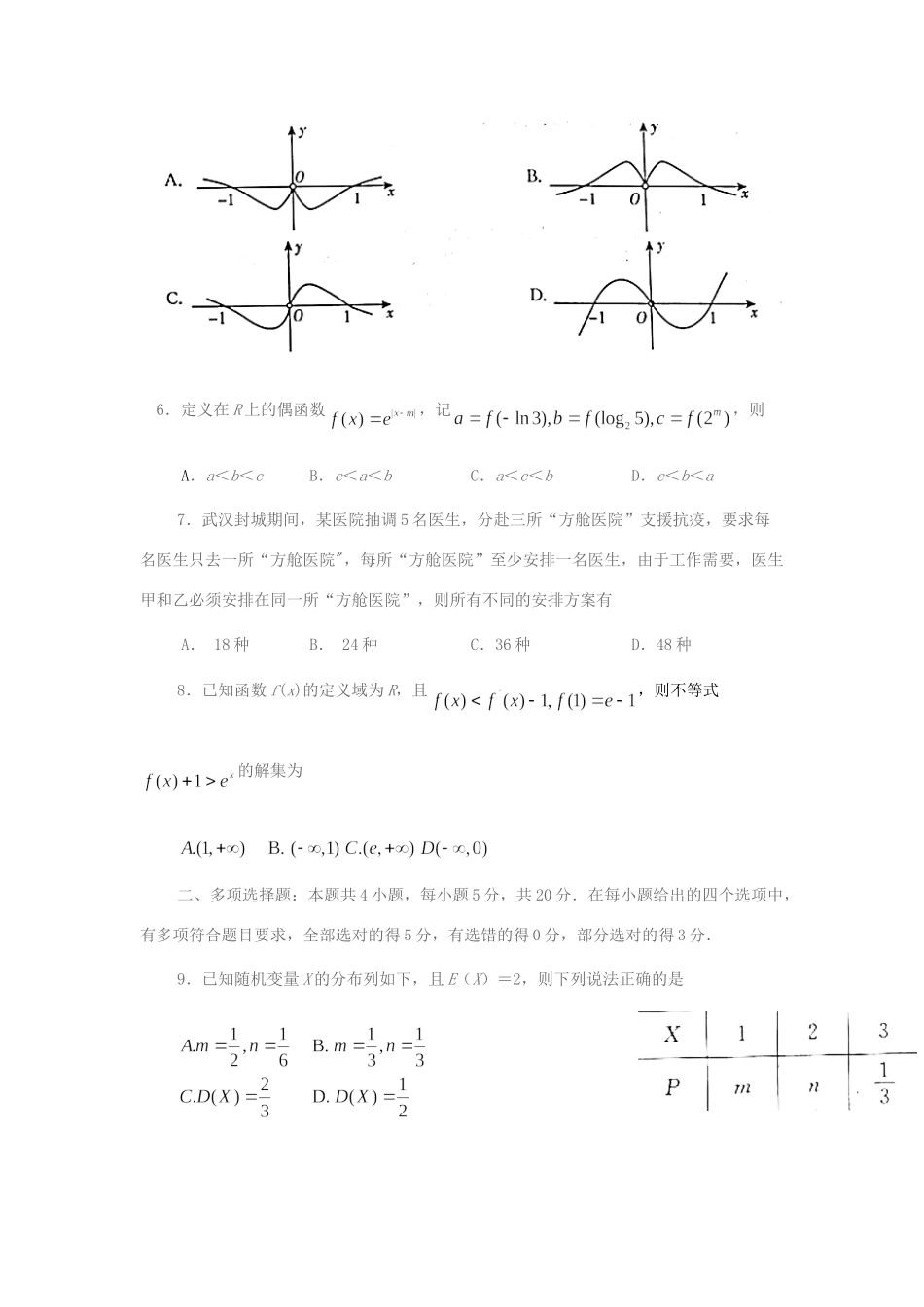
山东省济宁市2019-2020学年高二数学下学期期末考试试题第Ⅰ卷(选择题共60分)一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项符合题目要求.1.已知集合,则M∩N=2.随机变量,且P(X≥5)=0,2,则P(1≤X≤5)=A.0.6B.0.5C.0.4D.0.33.已知函数,则的值为4.函数的极大值点为5.函数的图象大致为6.定义在R上的偶函数,记,则A.a<b<cB.c<a<bC.a<c<bD.c<b<a7.武汉封城期间,某医院抽调5名医生,分赴三所“方舱医院”支援抗疫,要求每名医生只去一所“方舱医院",每所“方舱医院”至少安排一名医生,由于工作需要,医生甲和乙必须安排在同一所“方舱医院”,则所有不同的安排方案有A.18种B.24种C.36种D.48种8.已知函数f(x)的定义域为R,且,则不等式的解集为二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求,全部选对的得5分,有选错的得0分,部分选对的得3分.9.已知随机变量X的分布列如下,且E(X)=2,则下列说法正确的是10.若,则下列不等式一定成立的是11.为吸引顾客,某商场举办购物抽奖活动.抽奖规则是:从装有2个白球和3个红球(小球除颜色外,完全相同)的抽奖箱中,不放回地依次摸取两次,每次摸出一个球,记为一次抽奖.若摸出的2个球颜色相同则为中奖,否则为不中奖.下列随机事件的概率正确的是A.某顾客抽奖一次中奖的概率是B.某顾客抽奖三次,至少有一次中奖的概率是C.在一次抽奖过程中,若已知顾客第一次抽出了红球,则该顾客中奖的概率是D.在一次抽奖过程中,若已知顾客第一次抽出了红球,则该顾客中奖的概率是12.如果,不等式恒成立,则实数a的取值可以是A.2B.e-1C.1D.第Ⅱ卷(非选择题共90分)三、填空题:本题共4小题,每小题5分,共20分.13.的展开式中的常数项为________14.已知函数f(x)是定义在R上的奇函数,且满足,都有,当x∈[0,1]时,f(x)=2x-1,则f(15)=________15.已知一箱产品中有3件一等品,2件二等品,1件三等品.若从箱中任意取出3件产品检测,则抽出的3件产品中恰有1件一等品的概率是________.若从箱中逐一不放回地抽取产品进行检测,直到检测出三等品为止,当检测停止时,恰好取出了1件一等品的概率是________(本题第一空2分,第二空3分.)16.已知函数,若函数有6个零点,则实数a的取值范围是________四、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.17.(本小题满分10分)在①只有第6项的二项式系数最大,@第4项与第8项的二项式系数相等,③所有二项式系数的和为210,这三个条件中任选一个,补充在下面(横线处)问题中,解决下面两个问题.注:如果选择多个条件分别解答,按第一个解答计分.已知,若的展开式中,________(1)求n的值;(2)求的值.18.(本小题满分12分)在某校举办的“国学知识竞赛”决赛中,甲、乙两队各派出3名同学参加比赛.规则是:每名同学回答一个问题,答对为本队赢得1分,答错得0分.假设甲队中每名同学答对的概率均为,乙队中3名同学答对的概率分别是,且每名同学答题正确与否互不影响.用X表示乙队的总得分.(1)求随机变量X的分布列;(2)设事件A表示“甲队得2分,乙队得1分",求P(A).19.(本小题满分12分)在传染病学中,通常把从致病刺激物侵入机体或者对机体发生作用起,到机体出现反应或开始呈现该疾病对应的相关症状的这一阶段称为潜伏期.一研究团队统计了某地区200名患者的相关信息,得到如下表格(1)该传染病的潜伏期受诸多因索的影响,为研究潜伏期与患者年龄的关系,根据上表数据将如下列联表补充完整,并根据列联表判断是否有99%的把握认为该传染病的潜伏期与患者年龄有关.(2)将200名患者的潜伏期超过6天的频率视为该地区每名患者潜伏期超过6天发生的概率,每名患者的谱伏期是否超过6天相互独立,为了深入研究,该团队随机调查了该地区20名患者,其中潜伏期超过6天的人数为X,求随机变量X的期望和方差.附:,其中n=a+b+c+d.20.(本小题满分12分)定义在区间D上的函数f(x),若满足:,都有,则称f(x...