第二章单室模型-静脉滴注VIP免费

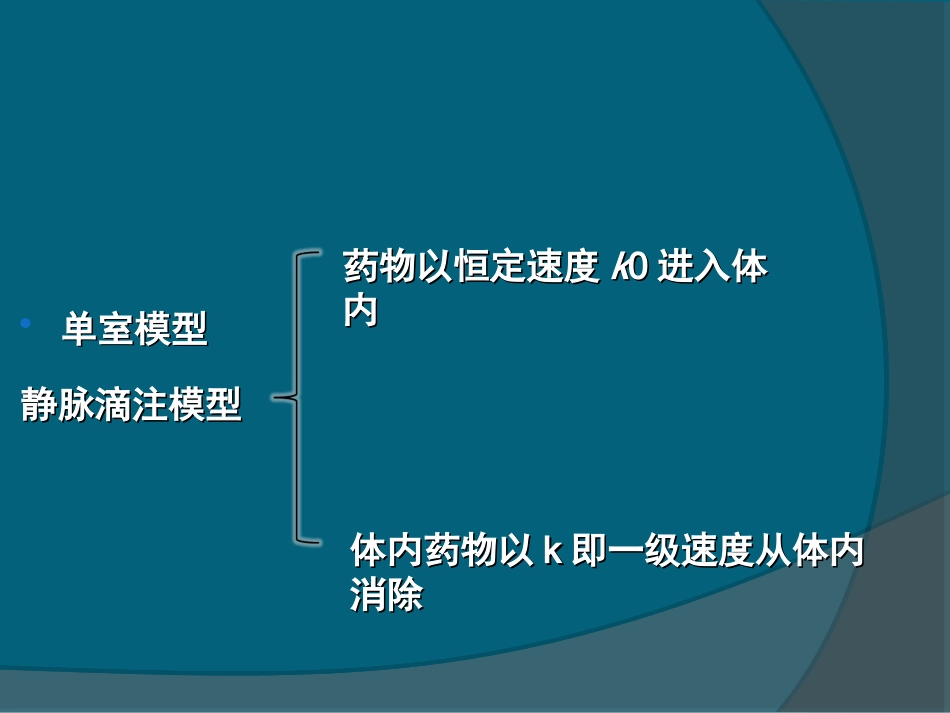
一、血药浓度一、血药浓度1.1.模型的建立模型的建立静脉滴注亦称静脉输注。是以恒定速向血管静脉滴注亦称静脉输注。是以恒定速向血管内给药的方式。单室模型药物以静脉滴往方式内给药的方式。单室模型药物以静脉滴往方式进人体内，在滴注时间进人体内，在滴注时间tt之内．体内除有消除过之内．体内除有消除过程外，同时存在一个恒速增加药量的过程，当程外，同时存在一个恒速增加药量的过程，当滴注完成后，体内才只有消除过程。滴注完成后，体内才只有消除过程。单室模型单室模型静脉滴注模型静脉滴注模型药物以恒定速度药物以恒定速度kk00进入体进入体内内体内药物以体内药物以kk即一级速度从体内即一级速度从体内消除消除XK0k单室模型静脉滴注给药示意图：因此，在0≤t≤T时间内，体内药物量X的变化情况，一方面以k0恒速增加，一方面从体内消除，药物从体内的消除速度与当时体内药物量的一次方成正比，体内药物的变化速度应该是这两部分的代数和，用微分方程表示为：式中，式中，dXdX／／dtdt为体内药物量为体内药物量XX的瞬时变的瞬时变化率；为零级静脉滴注速度常数，以单化率；为零级静脉滴注速度常数，以单位时间内的药量来表示；位时间内的药量来表示；kk为一级消除速度为一级消除速度常数常数kXkdtdX0(2-2-1)0k2、血药浓度和时间关系将（将（2-2-12-2-1）式经拉氏变换，得：）式经拉氏变换，得：整理后得：整理后得：XkSkXS0)(0kSSkX应用拉氏变换表解上式，可得：应用拉氏变换表解上式，可得：上式为单室模型静脉滴注给药，体内药量上式为单室模型静脉滴注给药，体内药量XX与时间与时间tt的函数关系式。的函数关系式。)1(0ktekkX(2-2-2)以以X=VCX=VC关系式代入，可得：关系式代入，可得：)1(0ktekVkC（（2-2-2-2-33））上上式即为单室模型静脉滴注给药，体内血药浓式即为单室模型静脉滴注给药，体内血药浓度度CC与时间与时间tt的函数关系式的函数关系式..3、稳态血药浓度(Css)从（2-2-3）式可见，在静脉滴注开始的一段时间内，血药浓度逐渐上升，然后趋近于一个恒定水平，此时的血药浓度值称为稳态血药浓度或称坪浓度，用Css表示。在达到稳态皿药浓度的状态下，体内药物的消除速度等于药物的输入速度。根据（根据（2-2-32-2-3）式，当）式，当t→∞t→∞时，时，ee-kt-kt→0,→0,(1-(1-ee-kt-kt)→1,)→1,则式中的血药浓度则式中的血药浓度CC用用CCssss来来表示。表示。kvkCSS0（（2-2-42-2-4））稳态血药浓度稳态血药浓度CCssss∝∝静滴速度静滴速度kk004.4.达稳态所需时间（达坪分数达稳态所需时间（达坪分数ffssss与半衰期与半衰期tt1/21/2的关的关系）系）静脉滴注给药时，达坪浓度以前的血药浓度静脉滴注给药时，达坪浓度以前的血药浓度CC一直小一直小于于CssCss，任何时间的，任何时间的CC值可用值可用CssCss某一分数来表示，某一分数来表示，即达坪分数，以即达坪分数，以ffssss表示，则：表示，则：ktktSSSSekvkekvkCCf1)1(00从上式可以看出．k愈大，滴注时间愈长，趋近于1愈快，即达到坪浓度愈快。换言之，药物的半衰期愈短，到达坪浓度亦愈快。以以tt1/21/2的个数的个数nn来表示时，来表示时，达到坪浓度某一分数达到坪浓度某一分数所需要的所需要的nn值，不论何种药物都是一样的值，不论何种药物都是一样的，不，不论论tt1/21/2长短如何。例如，达到长短如何。例如，达到CssCss的的90%90%需需3.33.3个个tt1/21/2，达到，达到CssCss的的95%95%需需4.34.3个个tt1/21/2。。nnttkt693.0693.02/12/1（（2-2-2-2-55））)1()1()1(693.0693.000nSSnkteCevkkekVkCssnSSfeCC693.01)1lg(32.3SSfn以以t1/2t1/2的个数的个数nn来表示时，来表示时，达到坪浓度某一分数所需达到坪浓度某一分数所需要的要的nn值，不论何种药物值，不论何种药物都是一样的，不论都是一样的，不论t1/2t1/2长长短如何短如何。。半衰期个数（n）达坪浓度（Css%）半衰期个数（n）达坪浓度（Css%）150596.88275698.44387.56.64993.3290799.22493.75899.61表静脉滴注半衰期个数与达坪浓度分数...