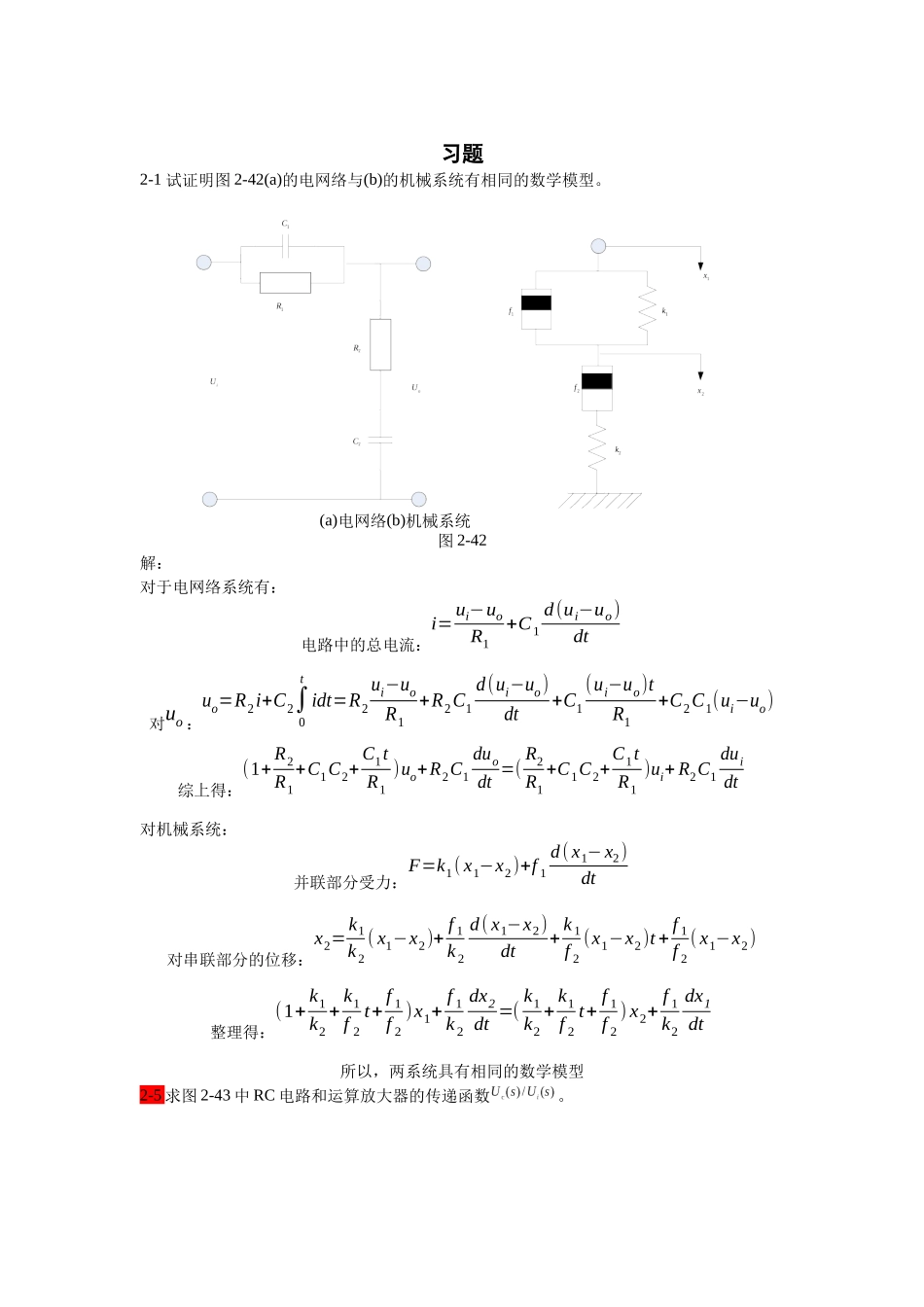
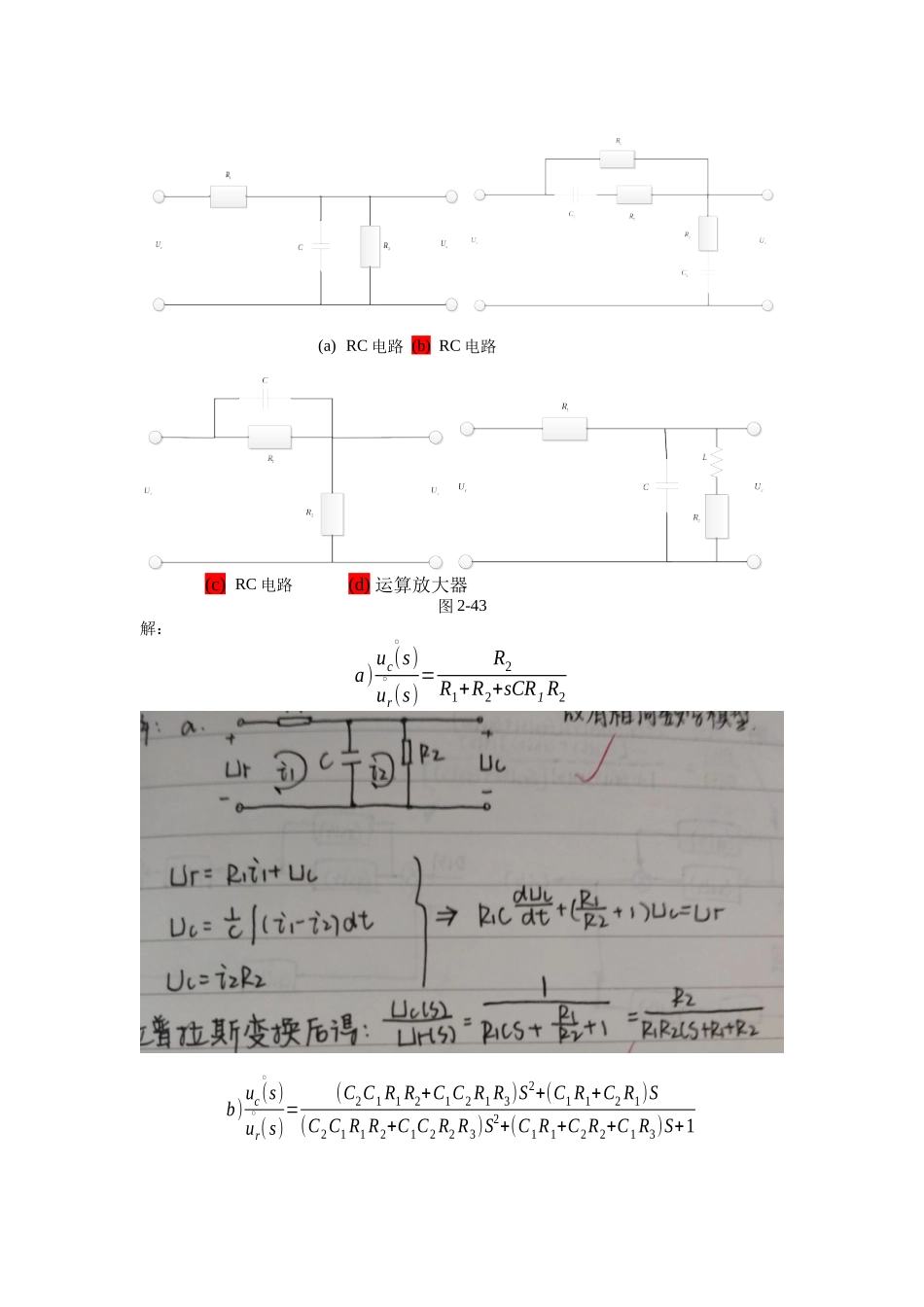
习题2-1试证明图2-42(a)的电网络与(b)的机械系统有相同的数学模型。(a)电网络(b)机械系统图2-42解:对于电网络系统有:电路中的总电流:i=ui−uoR1+C1d(ui−uo)dt对uo:uo=R2i+C2∫0tidt=R2ui−uoR1+R2C1d(ui−uo)dt+C1(ui−uo)tR1+C2C1(ui−uo)综上得:(1+R2R1+C1C2+C1tR1)uo+R2C1duodt=(R2R1+C1C2+C1tR1)ui+R2C1duidt对机械系统:并联部分受力:F=k1(x1−x2)+f1d(x1−x2)dt对串联部分的位移:x2=k1k2(x1−x2)+f1k2d(x1−x2)dt+k1f2(x1−x2)t+f1f2(x1−x2)整理得:(1+k1k2+k1f2t+f1f2)x1+f1k2dx2dt=(k1k2+k1f2t+f1f2)x2+f1k2dx1dt所以,两系统具有相同的数学模型2-5求图2-43中RC电路和运算放大器的传递函数。(a)RC电路(b)RC电路(c)RC电路(d)运算放大器图2-43解:a)uc(s)∘ur∘(s)=R2R1+R2+sCR1R2b)uc(s)∘ur∘(s)=(C2C1R1R2+C1C2R1R3)S2+(C1R1+C2R1)S(C2C1R1R2+C1C2R2R3)S2+(C1R1+C2R2+C1R3)S+1c)uc(s)∘ur∘(s)=R2CS+R1R2(CR1+CR2)S+R1R2d)uc(s)∘ur∘(s)=LS+R2(LR1+R1CR2)S+R1R2+LCR1S22-6求图2-44所示系统的传递函数C(s)/D(s)和E(s)/D(s)。图2-44系统结构框图解:C(s)D(s)=G2(s)+G3(s)1+G1(s)G2(s)H(s)+G1(s)G3(s)H(s)E(s)R(s)=−H(s)G2(s)−H(s)G3(s)1+G1(s)G2(s)H(s)+G1(s)G3(s)H(s)2-7由运算放大器组成的控制系统模拟电路如图2-45所示,试求闭环传递函数。图2-45控制系统结构框图2-102-112-12试简化图2-49中的系统结构图,并求传递函数C(s)/R(s)和C(s)/N(s)。图2-49系统结构框图解:a)令N(s)=0,C(s)R(s)=G1(s)G2(s)1+G1(s)G2(s)H(s)+G1(s)G2(s)令R(s)=0,C(s)N(s)=G1(s)G2(s)H(s)+G1(s)G2(s)G3(s)+11+G1(s)G2(s)H(s)+G1(s)G2(s)b)令N(s)=0,C(s)R(s)=G1(s)G2(s)G3(s)+G3(s)G2(s)+G4(s)G3(s)1+G3(s)G2(s)+G3(s)G4(s)令R(s)=0,C(s)N(s)=G3(s)1+G3(s)G2(s)+G3(s)G4(s)2-14求图2-51所示的系统的闭环传递函数C(s)/R(s)。图2-51系统结构框图解:C(s)R(s)=k1k5s+k2k3k5Ts3+k2k3k5+k3k4s+s2(1+k3k4T)2-17试用梅森增益公式求图2-54中各系统信号流图的传递函数C(s)/R(s)。(a)(b)图2-54系统信号流图解:a)L1=10∗−1=−10,L2=1∗−2=−2,L3=−0.5=》∑LiLj=5,∴Δ=1−(L1+L2+L3)+∑LiLj=19.5P1=1∗10∗2∗1=20,Δ1=1−(−10)=11P2=1∗5∗10∗1=50,Δ2=1+0.5=1.5C(s)R(s)=20∗11+50∗1.519.5=15.128b)L1=af,L2=gb,L3=ch,L4=ehgf∑LiLj=afch,∴Δ=1−af−bg−ch−ehgf+afchP1=abcd,Δ1=1P2=ed,Δ2=1−bgC(s)R(s)=abcd−ebdg+ed1−af−bg−ch−ehgf+afch2-20已知各系统的脉冲响应函数,试求系统的传递函数G(s)。(1)g(t)=;(2)g(t)=。解:(1)G(s)=0.125s+1.25(2)G(s)=2s2+15s2+9eπ9s