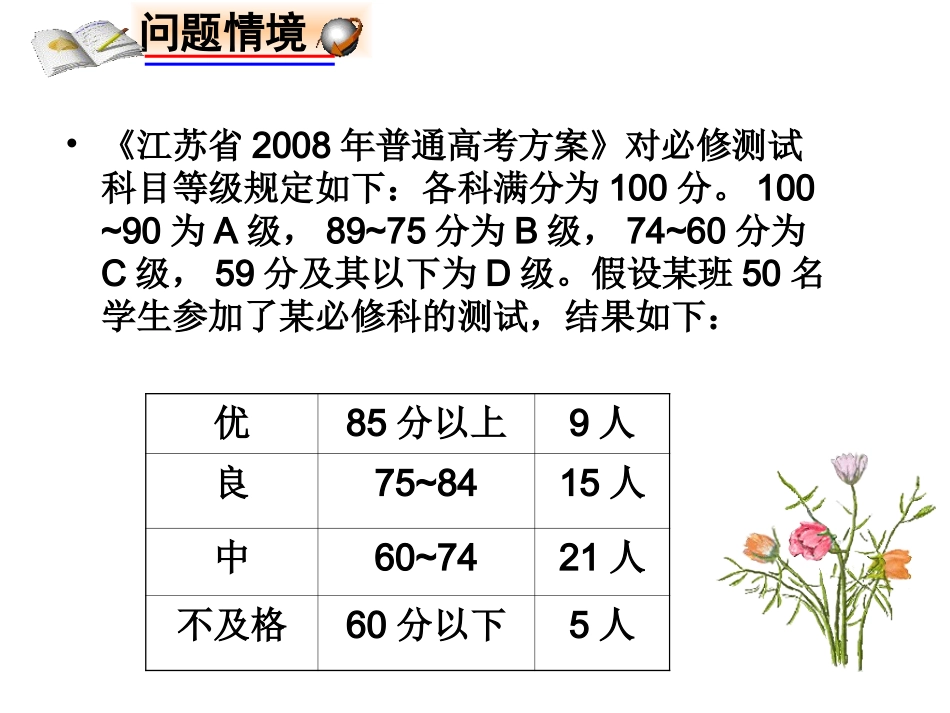
§3.4.1互斥事件及其发生的概率必修系列·数学31、求一个事件发生的概率的基本方法:dD的测度的测度复习回顾2、古典概型的事件A发生的概率为:进行大量的试验,用这个事件发生的频率近似的作为他的概率.P(A)=mn3、几何概型事件A发生的概率为:P(A)=•《江苏省2008年普通高考方案》对必修测试科目等级规定如下:各科满分为100分。100~90为A级,89~75分为B级,74~60分为C级,59分及其以下为D级。假设某班50名学生参加了某必修科的测试,结果如下:问题情境优85分以上9人良75~8415人中60~7421人不及格60分以下5人•问题1:在同一次考试中,某一位同学能否既得优又得良?问题2:如果将“测试成绩合格”记为事件E,那么E与D能否同时发生?它们之间有什么关系?问题3:从这个班任意抽取一位同学,那么这位同学的测试成绩为“优”的概率,为“良”的概率,为“优良”(优或良)的概率分别是多少?不能不能优:0.18;良:0.3;优良:0.18+0.3=0.48•1、互斥事件(1)概念:如果事件A和事件B不可能同时发生(即事件A发生,事件B不发生,事件B发生,事件A不发生),那么称事件A与B为互斥事件,互斥事件也叫做互不相容事件。讲授新课例如:上述例题中的事件A、B、C、D其中任意两个都是互斥的。互斥事件有什么性质?•(1)如果两个事件A与B互斥,那么由A,B所包含的结果所组成的集合的交集是空集;•(2)如果事件A,B是互斥事件,那么在事件讨论的全过程中,A与B同时发生的机会一次都没有,即A与B发生与否有三种可能:A发生,B不发生;A不发生,B发生;A,B都不发生。推广:一般的,如果事件1,2,3,.......nAAAA中的任何两个都是互斥的,那么就说事件12,,......nAAA彼此互斥。你能举出生活中一些彼此互斥的例子吗?例1抛掷一颗骰子一次,记“向上的点数是4,5,6”为事件A,“向上的点数是1,2”为事件B,“向上的点数为1,2,3”为事件C,“向上的点数是1,2,3,4”,为事件D,判别下列每件事件是不是互斥事件.(1)A与B(2)A与C(3)A与D(1)是互斥事件(2)是互斥事件(3)不是互斥事件解:变式训练:一个射手进行一次射击,记“命中的环数大于8”为事件A,“命中环数大于5”为事件B,“命中环数小于4”为事件C,“命中环数小于6”为事件D,那么A、B、C、D中有多少对互斥事件?解:是互斥事件的有:A与C,A与D,B与C,B与D例2一个盒内放有10个大小相同的小球,其中有7个红球,2个绿球,1个黄球,从中任取一个球。求:(1)得到红球的概率;(2)得到绿球的概率;(3)得到红球或者绿球的概率。710解:设从中任去一个球,摸到红球为事件A,摸到绿球为事件B,则摸到红球或者绿球为事件A+B则P(A)=P(B)=210P(A+B)=2791010由此我们看到:P(A+B)=P(A)+P(B)即即PP((AA++BB)=)=PP((AA)+)+PP((BB))如果事件如果事件AA,,BB是互斥事件,那么事件是互斥事件,那么事件AA++BB发生(即发生(即AA,,BB中有一个发生)的概率,等于事件中有一个发生)的概率,等于事件AA,,BB分别发生的概率的和。分别发生的概率的和。重要结论:一般地,如果事件一般地,如果事件AA11,,AA22,…,,…,AAnn彼此互彼此互斥,那么事件斥,那么事件AA11++AA22+…++…+AAnn发生(即发生(即AA11,,AA22,…,,…,AAnn中有一个发生)的概率,等于这中有一个发生)的概率,等于这nn个事件分别发生的概率的和,即个事件分别发生的概率的和,即PP((AA11++AA22+…++…+AAnn)=P(A)=P(A11)+P(A)+P(A22)+…+P)+…+P(A(Ann))2、对立事件(1)概念:如果A与B是互斥事件,且在一次试验中A与B必有一个发生,则称它们为对立事件,事件A的对立事件记为A(2)对立事件与互斥事件有什么不同的呢?对立事件是相对于两个互斥事件来说的,在一次试验中,不可能同时发生的事件是互斥事件,两个互斥事件可能发生一个,也可能都不发生,而对立事件则必须有一个发生,但不可能同时发生,所以两个事件互斥,不一定对立,反之,两个事件对立,它们一定互斥。总之,它们的共同点是:不可能同时发生;异同点是:对立一定互斥,互斥不一定对立。概念理解:•判断下列给出的每对事件,是否为互斥事件,是否...