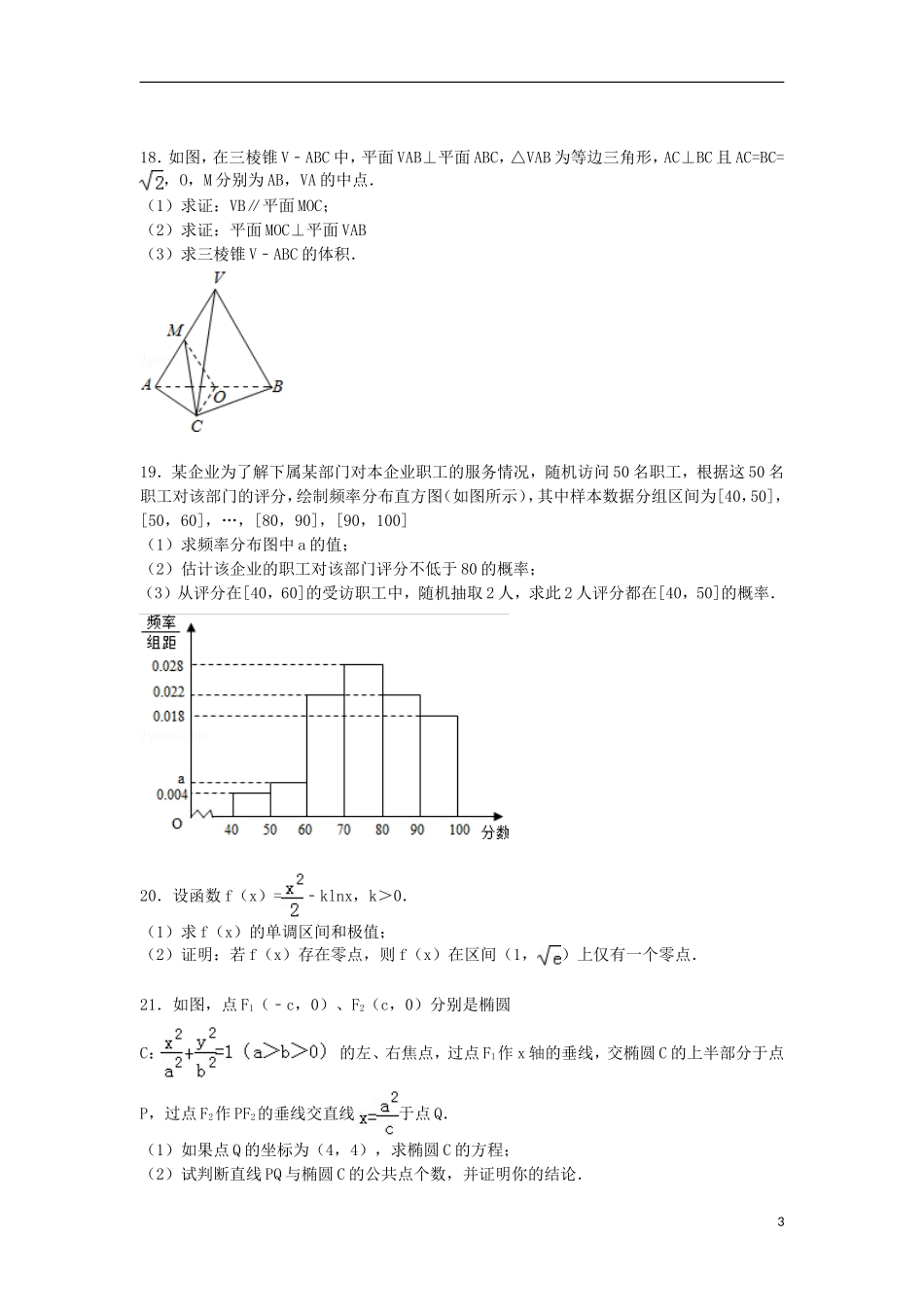
2014-2015学年湖南省衡阳市衡阳县三中高二(下)期末数学试卷(文科)一、选择题(共10小题,每小题5分,共50分)1.已知i是虚数单位,则2i(1+i)=()A.﹣2+2iB.2+2iC.2iD.﹣2i2.已知α的顶点在原点,始边与x轴的非负半轴重合,终边过点的值为()A.B.C.D.3.曲线y=2x3﹣3x+1在点(1,0)处的切线方程为()A.y=4x﹣5B.y=﹣3x+2C.y=﹣4x+4D.y=3x﹣34.已知命题p:∀x∈R,cosx≤1,则()A.¬p:∃x∈R,cosx≥1B.¬p:∃x∈R,cosx<1C.¬p:∃x∈R,cosx≤1D.¬p:∃x∈R,cosx>15.某四棱锥的三视图如图所示,该四棱锥最长棱的棱长为()A.1B.C.D.26.若不等式组表示的平面区域是一个三角形,则实数a的取值范围是()A.{a|1≤a≤3或a>5}B.{a|1<a≤3或a≥5}C.{a|1<a≤5}D.{a|3≤a≤5}17.已知定义在R上的函数f(x)的对称轴为x=﹣3,且当x≥﹣3时,f(x)=2x﹣3.若函数f(x)在区间(k﹣1,k)(k∈Z)上有零点,则k的值为()A.2或﹣7B.2或﹣8C.1或﹣7D.1或﹣88.设=(1,2),=(1,1),=+k,若,则实数k的值等于()A.﹣B.﹣C.D.9.当x∈[﹣2,1]时,不等式ax3﹣x2+4x+3≥0恒成立,则实数a的取值范围是()A.[﹣5,﹣3]B.[﹣6,﹣]C.[﹣6,﹣2]D.[﹣4,﹣3]10.已知直线y=mx与函数y=f(x)=的图象恰好有3个不同的公共点,则实数m的取值范围是()A.(,4)B.C.D.二、填空题(共5小题,每小题5分,共25分)11.已知集合A={1,2,3},B={2,4,5},则集合A∪B中元素的个数为.12.在等差数列{an}中,若a3+a4+a5+a6+a7=25,则a2+a8=.13.在△ABC中,a=3,b=,∠A=,则∠B=.14.不等式|x﹣1|﹣|x﹣5|<2的解集是.15.已知M(x0,y0)是双曲线C:﹣y2=1上的一点,F1、F2是C上的两个焦点,若•<0,则y0的取值范围是.三、解答题16.已知函数f(x)=(sinx+cosx)2+cos2x(1)求f(x)最小正周期;(2)求f(x)在区间上的最大值和最小值.17.已知等差数列{an}满足a1+a2=10,a4﹣a3=2(1)求{an}的通项公式;(2)设等比数列{bn}满足b2=a3,b3=a7,问:b6与数列{an}的第几项相等?218.如图,在三棱锥V﹣ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=,O,M分别为AB,VA的中点.(1)求证:VB∥平面MOC;(2)求证:平面MOC⊥平面VAB(3)求三棱锥V﹣ABC的体积.19.某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50],[50,60],…,[80,90],[90,100](1)求频率分布图中a的值;(2)估计该企业的职工对该部门评分不低于80的概率;(3)从评分在[40,60]的受访职工中,随机抽取2人,求此2人评分都在[40,50]的概率.20.设函数f(x)=﹣klnx,k>0.(1)求f(x)的单调区间和极值;(2)证明:若f(x)存在零点,则f(x)在区间(1,)上仅有一个零点.21.如图,点F1(﹣c,0)、F2(c,0)分别是椭圆C:的左、右焦点,过点F1作x轴的垂线,交椭圆C的上半部分于点P,过点F2作PF2的垂线交直线于点Q.(1)如果点Q的坐标为(4,4),求椭圆C的方程;(2)试判断直线PQ与椭圆C的公共点个数,并证明你的结论.342014-2015学年湖南省衡阳市衡阳县三中高二(下)期末数学试卷(文科)参考答案与试题解析一、选择题(共10小题,每小题5分,共50分)1.已知i是虚数单位,则2i(1+i)=()A.﹣2+2iB.2+2iC.2iD.﹣2i考点:复数代数形式的乘除运算.专题:数系的扩充和复数.分析:根复数的基本运算进行求解即可.解答:解:2i(1+i)=2i+2i2=﹣2+2i,故选:A点评:本题主要考查复数的基本运算,比较基础.2.已知α的顶点在原点,始边与x轴的非负半轴重合,终边过点的值为()A.B.C.D.考点:任意角的三角函数的定义.专题:计算题.分析:求出角的终边上的点到原点的距离,利用任意角的三角函数公式求出α的余弦值.解答:解: α的顶点在原点,始边与x轴的非负半轴重合又终边过点,此点到原点的距离为1∴故选D点评:解决角的终边上的点的问题,一般考虑任意角的三角函数公式.3.曲线y=2...