辽宁省沈阳二中11-12学年高二数学上学期12月月考 理【会员独享】VIP免费

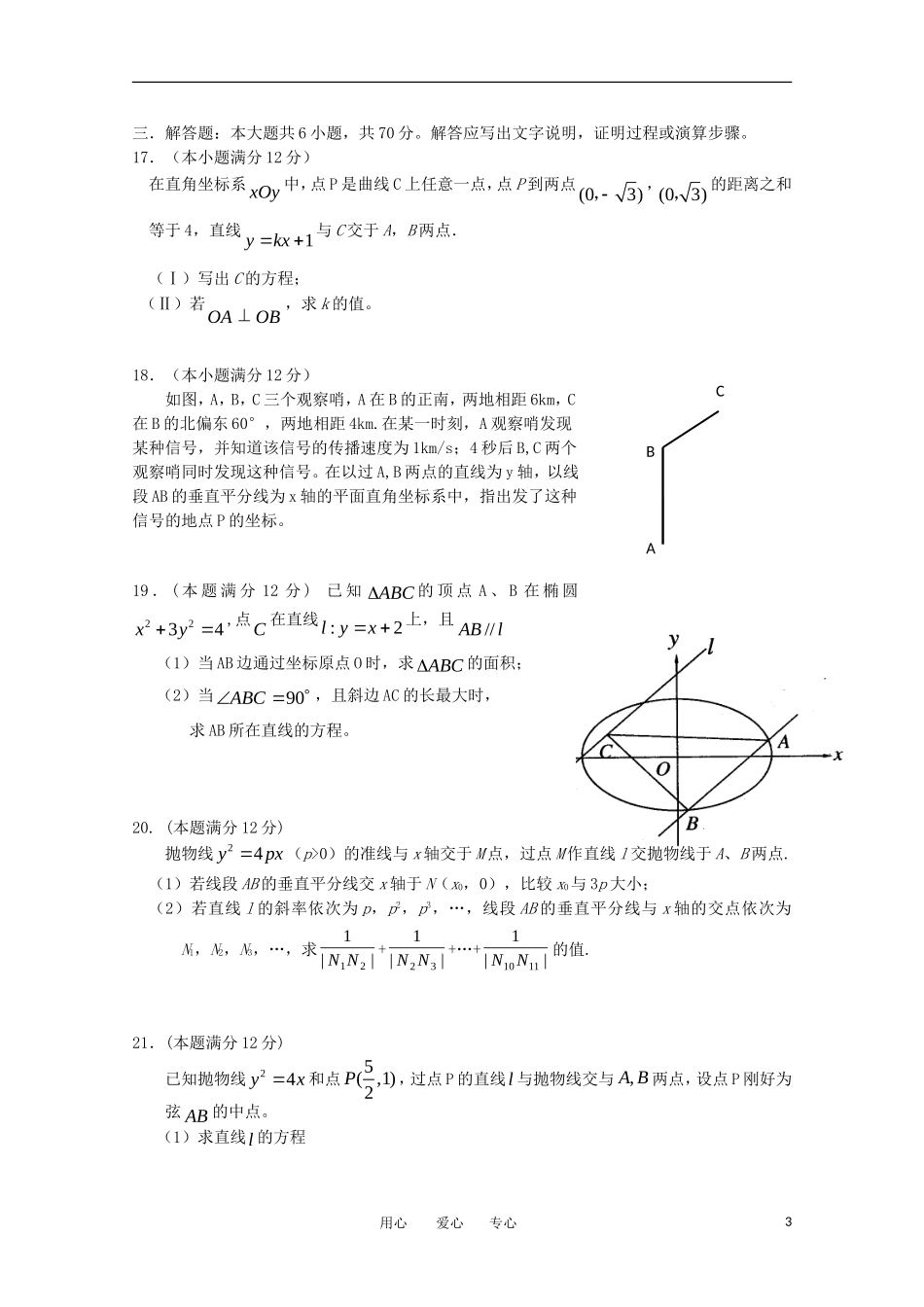
沈阳二中2011——2012学年度上学期12月月考高二（1３届）数学试题说明：1.测试时间：120分钟总分：150分2.客观题涂在答题纸上，主观题答在答题纸的相应位置上第Ⅰ卷（选择题共60分）1．“直线与双曲线有唯一交点”是“直线与双曲线相切”的()A.充分不必要条件B.必要不充分条件C.充要条件D.不充分不必要条件2.抛物线y2＝ax(a≠0)的焦点到其准线的距离是()A.B.C．|a|D．－3.抛物线212yx的准线与双曲线22193xy的两条渐近线所围成的三角形面积等于()A.33B.23C.2D.34．P是椭圆22143xy上任意一点，F1、F2是焦点，那么∠F1PF2的最大值是（）A．600B．300C．1200D．9005.已知F1,F2是椭圆的两个焦点，过F1且与椭圆长轴垂直的直线交椭圆于A,B两点，若△ABF2是正三角形，则这个椭圆的离心率是（）A．22B．23C．33D．326.已知a、b、c分别为双曲线的实半轴长、虚半轴长、半焦距，且方程02cbxax无实根，则双曲线离心率的取值范围是（）A.251aB.21eC.31eD.521e7.设a，b∈R，ab≠0，那么直线ax－y＋b＝0和曲线bx2＋ay2＝ab的图形是()ABCD8.若直线mx-ny=4与⊙O:x2+y2=4没有交点，则过点P(m,n)的直线与椭圆22194xy的交点个数是（）A．至多为1B．2C．1D．0用心爱心专心1yyyyxxxx9.若点（x，y）在椭圆2244xy上，则2xy的最小值为（）A.1B.－1C.－323D.以上都不对10.如图，F为抛物线24yx的焦点，A、B、C在抛物线上，若0FAFBFC�，则||||||FAFBFC�（）A.6B.4C.3D.211.椭圆有这样的光学性质：从椭圆的一个焦点出发的光线，经椭圆反射后，反射光线经过椭圆的另一个焦点，今有一个水平放置的椭圆形台球盘，点A、B是它的焦点，长轴长为2a，焦距为2c，静放在点A的小球（小球的半径不计），从点A沿直线出发，经椭圆壁反弹后第一次回到点A时，小球经过的路程是（）A．4aB．2()acC．2()acD．以上答案均有可能12.设经过定点(,0)Ma的直线与抛物线22ypx相交于,PQ两点，若2211||||PMQM为常数，则a的值为（）A．pB。2pC。2pD。2p第Ⅱ卷（非选择题共90分）13．若抛物线)0(22ppxy的焦点与双曲线2213xy的左焦点重合,则p的值.14.与双曲线221169xy有共同的渐近线，且经过点(23,3)A的双曲线的标准方程为15.过双曲线x2－122y的右焦点作直线交双曲线于A、B两点，且4AB，则这样的直线有___________条。16.P为双曲线22115yx右支上一点，M、N分别是圆2222(4)4(4)1xyxy和上的点，则|PM|-|PN|的最大值为用心爱心专心2xyoy三．解答题：本大题共6小题，共70分。解答应写出文字说明，证明过程或演算步骤。17．（本小题满分12分）在直角坐标系xOy中，点P是曲线C上任意一点，点P到两点(03)，，(03)，的距离之和等于4，直线1ykx与C交于A，B两点．（Ⅰ）写出C的方程；（Ⅱ）若OA�OB�，求k的值。18．（本小题满分12分）如图，A，B，C三个观察哨，A在B的正南，两地相距6km，C在B的北偏东60°，两地相距4km.在某一时刻，A观察哨发现某种信号，并知道该信号的传播速度为1km/s；4秒后B,C两个观察哨同时发现这种信号。在以过A,B两点的直线为y轴，以线段AB的垂直平分线为x轴的平面直角坐标系中，指出发了这种信号的地点P的坐标。19．(本题满分12分)已知ABC的顶点A、B在椭圆2234xy,点C在直线:2lyx上，且//ABl（1）当AB边通过坐标原点O时，求ABC的面积；（2）当90ABC，且斜边AC的长最大时，求AB所在直线的方程。20.(本题满分12分)抛物线24ypx（p>0）的准线与x轴交于M点，过点M作直线l交抛物线于A、B两点.（1）若线段AB的垂直平分线交x轴于N（x0，0），比较x0与3p大小；（2）若直线l的斜率依次为p，p2，p3，…，线段AB的垂直平分线与x轴的交点依次为N1，N2，N3，…，求||121NN+||132NN+…+||11110NN的值.21．(本题满分12分)已知抛物线24yx和点5(,1)2P，过点P的直线l与抛物线交与,AB两点，设点P刚好为弦AB的中点。（1）求直线l的方程用心爱心专心3CBA（2）若过线段AB上任一1P（不含端点,AB）作倾斜角为arctan2的直线l交抛物线于11,AB，类比圆中的相交弦定理，给出你的猜想，若成立，给出证明；若不成...