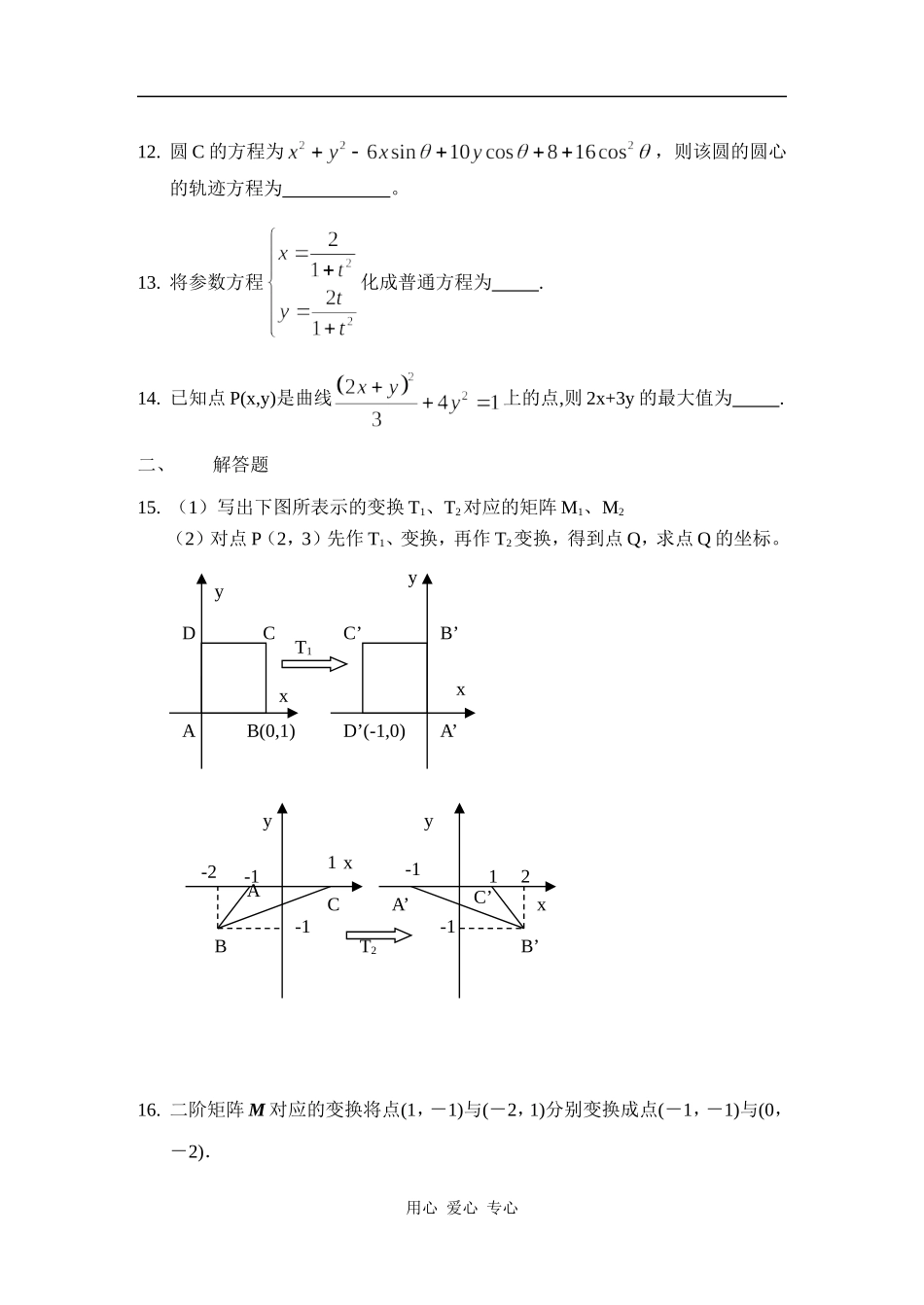
南京九中高二年级2009年5月月考数学试卷一、填空题(每小题5分,共70分)1.已知点P的极坐标是,将它化为直角坐标是.2.样本相关系数r越接近于1,变量x,y的线性相关程度越(填“强”或“弱”).3.抛掷两颗质量均匀的骰子各一次,则向上的点数之和是7时,其中有一个点数是2的概率是.4.某批产品中有20%的不合格,进行重复抽样检查,共取5个样品,其中不合格品数为X,则P(X>3)=.5.已知曲线经过伸压变换T作用后变为新的曲线,则变换T所对应的矩阵为.6.7.将平面内的点P(x,y)按顺时针方向旋转1200得到点P’(x’,y’),对应的变换矩阵可写为.8.将极坐标方程化为直角坐标方程为.9.过点且和极轴垂直的直线方程为.10.的圆心坐标为.11.在极坐标系中,极点到直线的距离是.用心爱心专心12.圆C的方程为,则该圆的圆心的轨迹方程为。13.将参数方程化成普通方程为.14.已知点P(x,y)是曲线上的点,则2x+3y的最大值为.二、解答题15.(1)写出下图所表示的变换T1、T2对应的矩阵M1、M2(2)对点P(2,3)先作T1、变换,再作T2变换,得到点Q,求点Q的坐标。16.二阶矩阵M对应的变换将点(1,-1)与(-2,1)分别变换成点(-1,-1)与(0,-2).用心爱心专心AB(0,1)CDA’B’C’D’(-1,0)T1-2-1-12-1-1CAB11A’B’C’xyyyyxxxT2(1)求矩阵M;(2)设直线l在变换M作用下得到了直线m:x-y=4,求l的方程.17.求直线的两个交点到点M(4,-1)的距离的和与积.18.某次乒乓球比赛的决赛在甲乙两名选手之间举行,比赛采用五局三胜制,按以往比赛经验,甲胜乙的概率为.(1)求恰好比赛三局甲获胜的概率;(2)求甲获胜的概率;(3)设甲比赛的次数为,求的数学期望.19.圆和圆的极坐标方程分别为.(1)把圆和圆的极坐标方程化为直角坐标方程;用心爱心专心(2)求经过圆,圆交点的直线的直角坐标方程.20.点P在曲线上,三角形OPQ为等腰直角三角形,∠OQP=900,求点Q的轨迹方程.南京九中高二年级2009年5月月考数学答题卷用心爱心专心一、填空题(每小题5分,共70分)1.;2.;3.;4.;5.;6.;;7..8.;9.;10..11.;12..13.;14..二、解答题15.(14分)写出下图所表示的变换T1、T2对应的矩阵M1、M2(2)对点P(2,3)先作T1、变换,再作T2变换,得到点Q,求点Q的坐标。16.(14分)二阶矩阵M对应的变换将点(1,-1)与(-2,1)分别变换成点(-1,-1)与(0,-2).(1)求矩阵M;(2)设直线l在变换M作用下得到了直线m:x-y=4,求l的方程.用心爱心专心AB(0,1)CDA’B’C’D’(-1,0)T1-2-1-12-1-1CAB11A’B’C’xyyyyxxxT217.(15分)求直线的两个交点到点M(4,-1)的距离的和与积.18.(15分)圆和圆的极坐标方程分别为.(1)把圆和圆的极坐标方程化为直角坐标方程;(2)求经过圆,圆交点的直线的直角坐标方程.用心爱心专心19.(16分)某次乒乓球比赛的决赛在甲乙两名选手之间举行,比赛采用五局三胜制,按以往比赛经验,甲胜乙的概率为.(1)求恰好比赛三局甲获胜的概率;(2)求甲获胜的概率;(3)设甲比赛的次数为,求的数学期望.20.(16分)点P在曲线上,三角形OPQ为等腰直角三角形,∠OQP=900,求点Q的轨迹方程.用心爱心专心南京九中高二年级2009年5月月考数学试卷参考答案一、填空题1、;2、强;3、;4、;5、;6、,用心爱心专心;7、8、x2+y2=0或x+1=0;9、;10、;11、;12、;13、(x-1)2+y2=1(x≠0);14、2二、解答题15、(1)(2)Q(-11,2)16、17、距离之和:;距离之积:818、(1)⊙O1(x-2)2+y2=4;⊙O2:x2+(y+2)2=4(2)y=-x19、用心爱心专心20、x2+y2+2y-1=0或x2+y2-2x-1=0.用心爱心专心