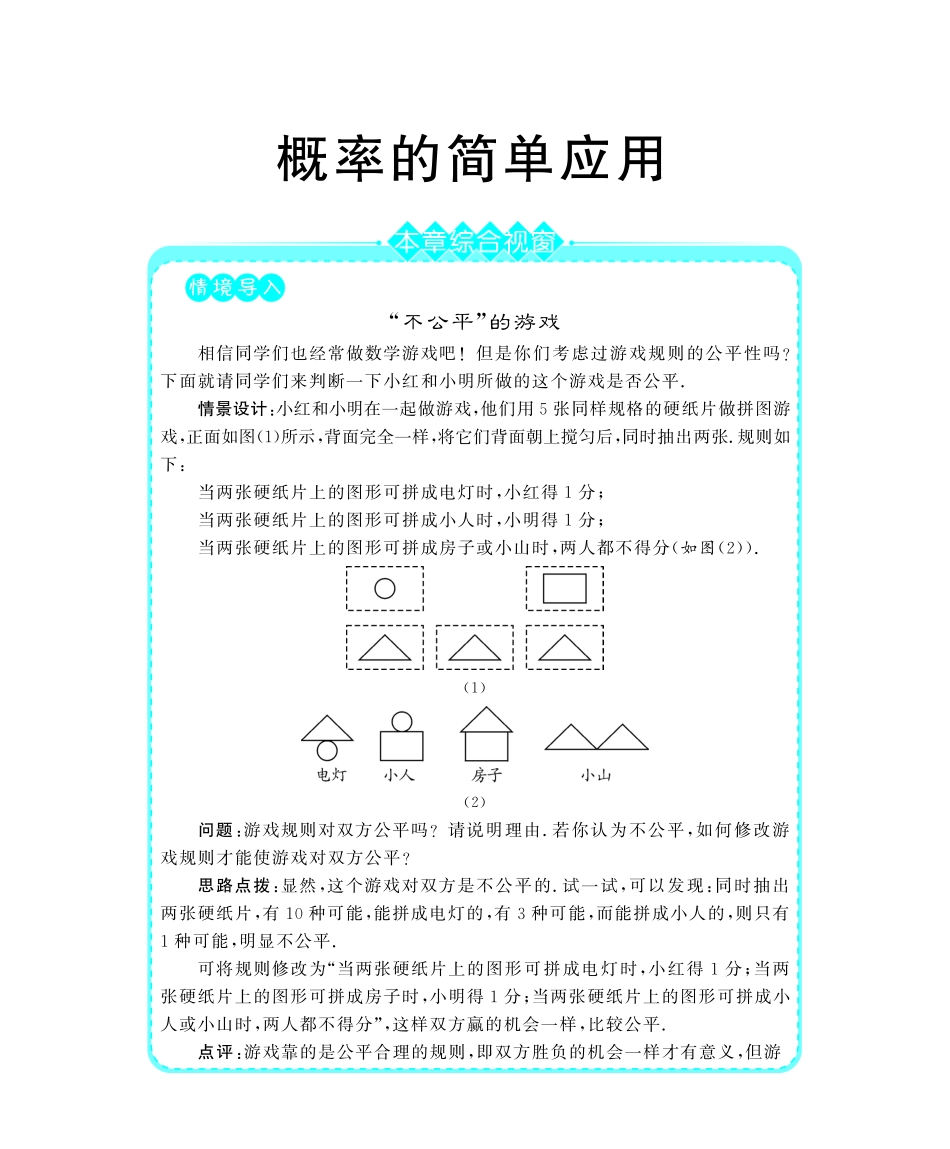
第九章概率的简单应用情境导入“不公平”的游戏相信同学们也经常做数学游戏吧!但是你们考虑过游戏规则的公平性吗?下面就请同学们来判断一下小红和小明所做的这个游戏是否公平.情景设计:小红和小明在一起做游戏,他们用5张同样规格的硬纸片做拼图游戏,正面如图(1)所示,背面完全一样,将它们背面朝上搅匀后,同时抽出两张.规则如下:当两张硬纸片上的图形可拼成电灯时,小红得1分;当两张硬纸片上的图形可拼成小人时,小明得1分;当两张硬纸片上的图形可拼成房子或小山时,两人都不得分(如图(2)).(1)(2)问题:游戏规则对双方公平吗?请说明理由.若你认为不公平,如何修改游戏规则才能使游戏对双方公平?思路点拨:显然,这个游戏对双方是不公平的.试一试,可以发现:同时抽出两张硬纸片,有10种可能,能拼成电灯的,有3种可能,而能拼成小人的,则只有1种可能,明显不公平.可将规则修改为“当两张硬纸片上的图形可拼成电灯时,小红得1分;当两张硬纸片上的图形可拼成房子时,小明得1分;当两张硬纸片上的图形可拼成小人或小山时,两人都不得分”,这样双方赢的机会一样,比较公平.点评:游戏靠的是公平合理的规则,即双方胜负的机会一样才有意义,但游戏过程的变化性、随机性使得游戏的结果也富有戏剧性.本章将告诉你:①学习的重点是:利用概率解决一些简单的实际问题.②本章的学习难点是:理解事件发生的频率与概率之间的关系.考点聚集专题1.对概率的认识.专题2.利用概率解决一些实际问题.方法指路1.对概率的认识应通过大量实例,特别是与我们的生活密切相关的例子来分析研究,纠正一些错误的认识也有利于对概率的认识.2.对概率的学习重点不在“如何计算概率”上,应通过典型的例子和实验不断发展随机观念,理解随机事件发生的不确定性,以及频率的稳定性,初步形成用随机观念观察和分析问题的意识.9.1抽签方法合理吗学习目标导航1.澄清日常生活中的一些错误认识.2.了解一些游戏的公平性.3.能利用概率解决一些简单的问题.教材知识详析要点1用列举法(列表法、树状图)计算一些随机事件在等可能条件下的概率例1将形状和大小都一样的红、白两种颜色的小球分装在甲、乙两个口袋中,甲袋装有1个红球和1个白球,乙袋装有2个红球和1个白球,现从每个口袋中各随机摸出1个小球.(1)请你用画树状图或列表的方法表示所有等可能的结果;(2)有人说:“摸出‘2红’和摸出‘1红1白’这两个事件发生的概率相等.”你同意这种说法吗,为什么?精析:用画树状图或列表的方法就是帮助我们不重复、不遗漏地列出所有可能出现的结果,对于口袋中2个红球可以记为“红1”和“红2”.解答:(解法一)列举所有等可能的结果,画树状图:图9.1G1(解法二)列表如下:甲袋乙袋红1红2白红红红1红红2红白白白红1白红2白白(2)不同意这种说法.由(1),知P(2红)=26=13,P(1红1白)=36=12,∴P(2红)<P(1红1白).有关概率的问题中,常常有类似(2)的不正确说法,想反驳这类错误认识的办法就是通过画树状图或列表把所有可能出现的结果一一列举出来.要点2游戏是否公平的问题游戏是否公平有时存在一定的隐蔽性,需要我们运用相关数学知识去分析、评判.如:抛掷一枚普通的硬币仅有两个可能的结果:“出现正面”和“出现反面”,这两个结果发生的机会相等,所以各占50%的机会,50%这个数表示事件“出现正面”发生的可能性大小.表示一个事件发生的可能性大小的这个数,叫做该事件的概率.通常,要判断一个游戏是否公平,则要考察事件发生的概率是否相同.图9.1G2例2张红和王伟两人争取一张观看北京奥运知识竞赛的入场券,张红设计了一个方案,方案是:转动如图9.1G2所示的转盘,如果指针停在阴影区域,则张红得到入场券;如果指针停在白色区域,则王伟得到入场券(转盘被等分成6个扇形.若指针停在边界处,则重新转动转盘).计算张红获得入场券的概率,并说明张红的方案是否公平.精析:转盘自由转动求概率时,先要弄清指针指向每个区域的机会是否均等,再根据转盘所占的份数确定概率.解答:因为P(白色)=36=12,P(阴影)=36=12,即P(白色)=P(阴影),所以P(张红获得入场券)=P(王伟获得...