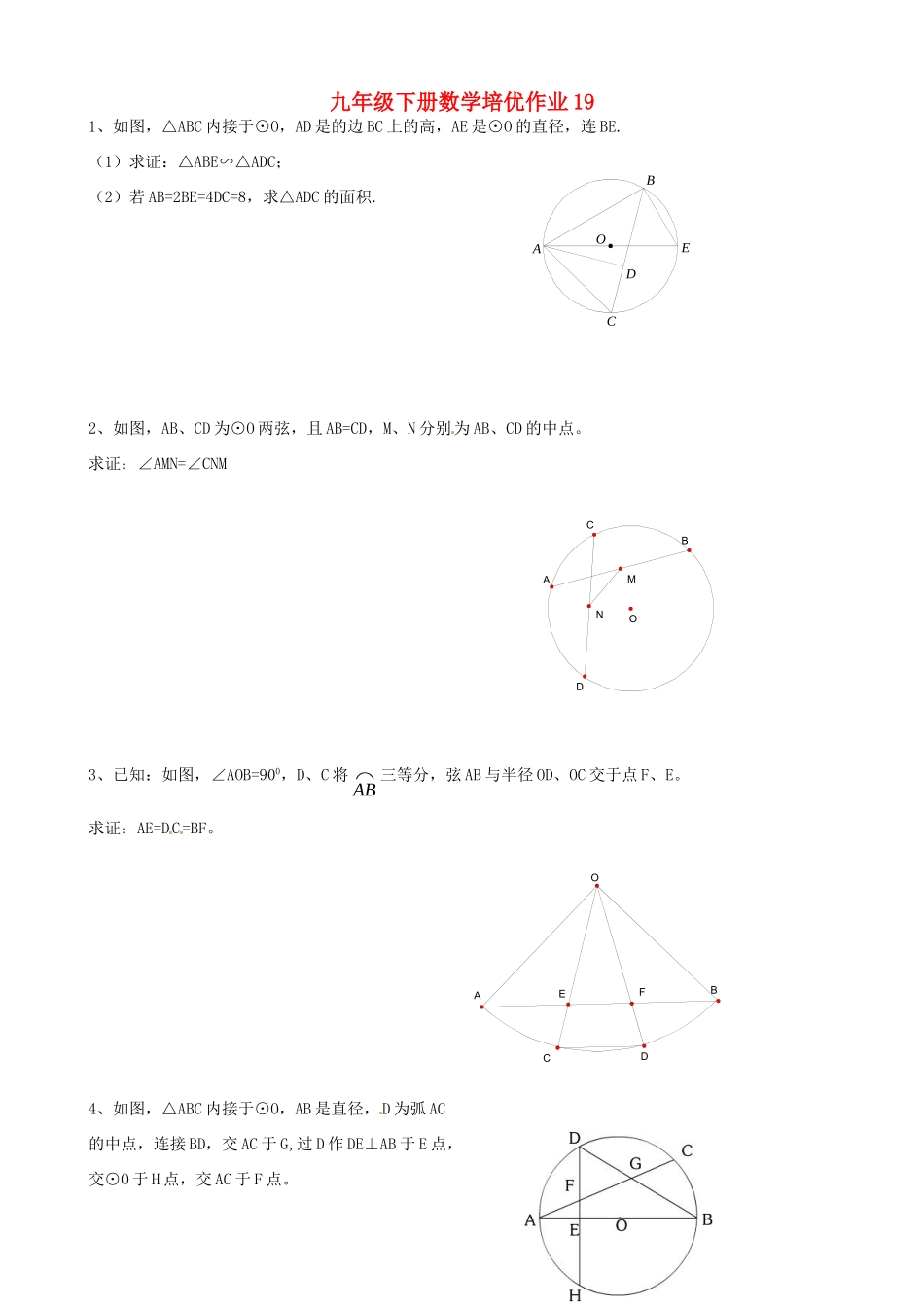
OABCDE九年级下册数学培优作业191、如图,△ABC内接于⊙O,AD是的边BC上的高,AE是⊙O的直径,连BE.(1)求证:△ABE∽△ADC;(2)若AB=2BE=4DC=8,求△ADC的面积.2、如图,AB、CD为⊙O两弦,且AB=CD,M、N分别为AB、CD的中点。求证:∠AMN=∠CNM3、已知:如图,∠AOB=900,D、C将⌒AB三等分,弦AB与半径OD、OC交于点F、E。求证:AE=DC=BF。4、如图,△ABC内接于⊙O,AB是直径,D为弧AC的中点,连接BD,交AC于G,过D作DE⊥AB于E点,交⊙O于H点,交AC于F点。NMDOABCCDEFBOA(1)、求证:FD=FG(2)、若AF·FC=32,ED=6,求ADFS。5、如图,AE是△ABC外接圆⊙O的直径,BC∥AE,过C点作CD⊥AE于D,CD交AB于F(1)求证:△ACF~△ABC;(2)若CF=2DF=2,AD=4,求⊙O的直径.6、如图,AE是△ABC外接圆⊙O的直径,若B、C在AE的同一侧,过C点作CD⊥AE于D,CD交AB于F。(1)求证:∠ACF=∠B;(2)若点B为弧CE的中点,CD=3AD=3,求ACBS的值.7、已知:如图等边ABC内接于⊙O,点P是劣弧PC上的一点(端点除外),延长BP至D,使BD=AP,连结CD.(1)若AP过圆心O,如图①,请你判断PDC是什么三角形?并说明理由.(2)若AP不过圆心O,如图②,PDC又是什么三角形?为什么?CDBFEOACDBFEOAAOCDPB图①AOCDPB图②8、(1)如图OA、OB是⊙O的两条半径,且OA⊥OB,点C是OB延长线上任意一点:过点C作CD切⊙O于点D,连结AD交DC于点E.求证:CD=CE(2)若将图中的半径OB所在直线向上平行移动交OA于F,交⊙O于B’,其他条件不变,那么上述结论CD=CE还成立吗?为什么?(3)若将图中的半径OB所在直线向上平行移动到⊙O外的CF,点E是DA的延长线与CF的交点,其他条件不变,那么上述结论CD=CE还成立吗?为什么9、在直径为AB的半圆内,划出一块三角形区域,如图所示,使三角形的一边为AB,顶点C在半圆圆周上,其它两边分别为6和8,现要建造一个内接于△ABC的矩形水池DEFN,其中D、E在AB上,如图24-94的设计方案是使AC=8,BC=6.(1)求△ABC的边AB上的高h.(2)设DN=x,且ABNFhDNh,当x取何值时,水池DEFN的面积最大?(3)实际施工时,发现在AB上距B点1。85的M处有一棵大树,问:这棵大树是否位于最大矩形水池的边上?如果在,为了保护大树,请设计出另外的方案,使内接于满足条件的三角形中欲建的最大矩形水池能避开大树.hFDECBANG