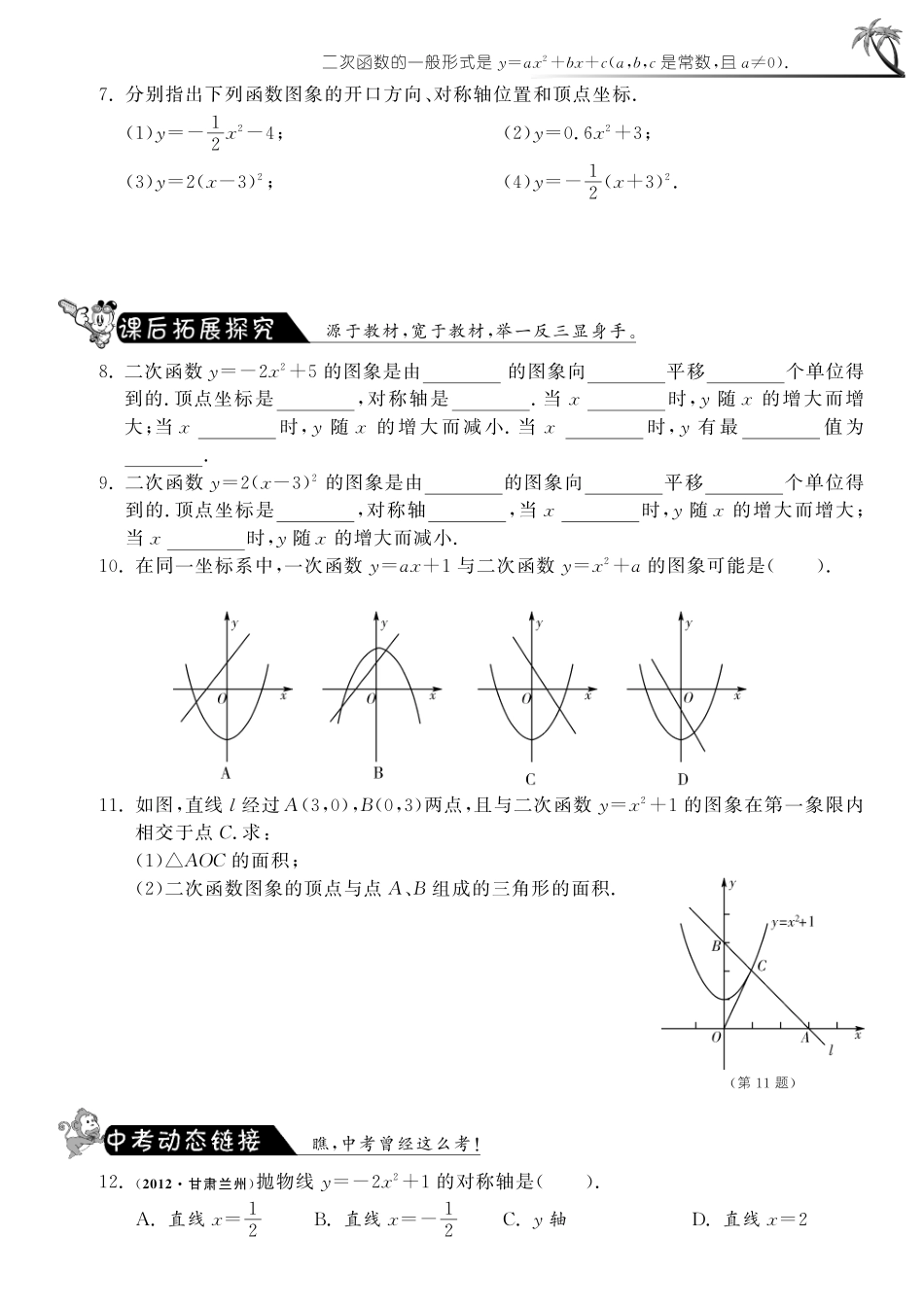
第3课时形如y=ax2+k(a≠0)、y=a(x-h)2(a≠0)的二次函数的图象与性质1.会用描点法画出二次函数y=ax2+k与y=a(x-h)2(a≠0)的图象.2.能结合图象确定抛物线y=ax2+k与y=a(x-h)2(a≠0)的对称轴与顶点坐标.3.掌握二次函数y=ax2+k与y=a(x-h)2(a≠0)的图象与二次函数y=ax2(a≠0)的图象的关系.开心预习梳理,轻松搞定基础.1.在同一平面直角坐标系中画出二次函数y=x2,y=x2+1,y=x2-1的图象,由图象回答下列问题:(1)抛物线y=x2的开口方向、对称轴与顶点坐标分别是什么?(2)抛物线y=x2-1的开口方向、对称轴与顶点坐标分别是什么?(3)抛物线y=x2+1,y=x2-1与y=x2的开口方向、对称轴、顶点坐标有何异同?(4)抛物线y=x2+1是由抛物线y=x2沿y轴怎样移动得到的?抛物线y=x2-1呢?2.在同一平面直角坐标系中画出二次函数y=2x2,y=2(x-1)2,y=2x2-1的图象.二次函数y=2(x-1)2,y=2x2-1的图象与函数y=2x2的图象有什么关系?重难疑点,一网打尽.3.在抛物线y=-x2+1上的一个点是().A.(1,0)B.(0,0)C.(0,-1)D.(1,1)4.二次函数y=-7(x-1)2的图象的开口向,顶点坐标为,对称轴为,它可以看作是由二次函数y=-7x2的图象向平移个单位长度得到的.5.二次函数y=-12x2+3的图象的对称轴是,顶点坐标是,它可以看作是由二次函数y=-12x2的图象向平移个单位长度得到的,当x=时,函数值最,最值是.6.将抛物线y1=2x2向右平移2个单位,得到抛物线y2的图象,则y2=.二次函数的一般形式是y=ax2+bx+c(a,b,c是常数,且a≠0).7.分别指出下列函数图象的开口方向、对称轴位置和顶点坐标.(1)y=-12x2-4;(2)y=0.6x2+3;(3)y=2(x-3)2;(4)y=-12(x+3)2.源于教材,宽于教材,举一反三显身手.8.二次函数y=-2x2+5的图象是由的图象向平移个单位得到的.顶点坐标是,对称轴是.当x时,y随x的增大而增大;当x时,y随x的增大而减小.当x时,y有最值为.9.二次函数y=2(x-3)2的图象是由的图象向平移个单位得到的.顶点坐标是,对称轴,当x时,y随x的增大而增大;当x时,y随x的增大而减小.10.在同一坐标系中,一次函数y=ax+1与二次函数y=x2+a的图象可能是().11.如图,直线l经过A(3,0),B(0,3)两点,且与二次函数y=x2+1的图象在第一象限内相交于点C.求:(1)△AOC的面积;(2)二次函数图象的顶点与点A、B组成的三角形的面积.(第11题)瞧,中考曾经这么考!12.(2012甘肃兰州)抛物线y=-2x2+1的对称轴是().A.直线x=12B.直线x=-12C.y轴D.直线x=2第3课时1.图略(1)开口向上,对称轴为y轴,顶点坐标为(0,0).(2)开口向上,对称轴为y轴,顶点坐标为(0,-1).(3)开口方向都向上,对称轴都是y轴,顶点坐标不同,分别为(0,1),(0,-1),(0,0).(4)y=x2+1的图象是由y=x2的图象向上平移1个单位长度得到的;y=x2-1的图象是由y=x2的图象向下平移1个单位长度得到的.2.图略y=2(x-1)2的图象是由y=2x2的图象向右平移1个单位长度得到的.y=2x2-1的图象是由y=2x2的图象向下平移1个单位长度得到的.3.A4.下(1,0)x=1右15.x=0(0,3)上30大大36.2(x-2)2或2x2-8x+87.(1)开口向下,对称轴是y轴,顶点坐标为(0,-4).(2)开口向上,对称轴是y轴,顶点坐标为(0,3).(3)开口向上,对称轴直线x=3,顶点坐标为(3,0).(4)开口向下,对称轴是直线x=-3,顶点坐标为(-3,0).8.y=-2x2上5(0,5)y轴<0>0=0大59.y=2x2右3(3,0)直线x=3>3<310.C11.(1)直线l的解析式为y=-x+3,点C的坐标为(1,2),故S△AOC=12OAyC=3.(2)212.C