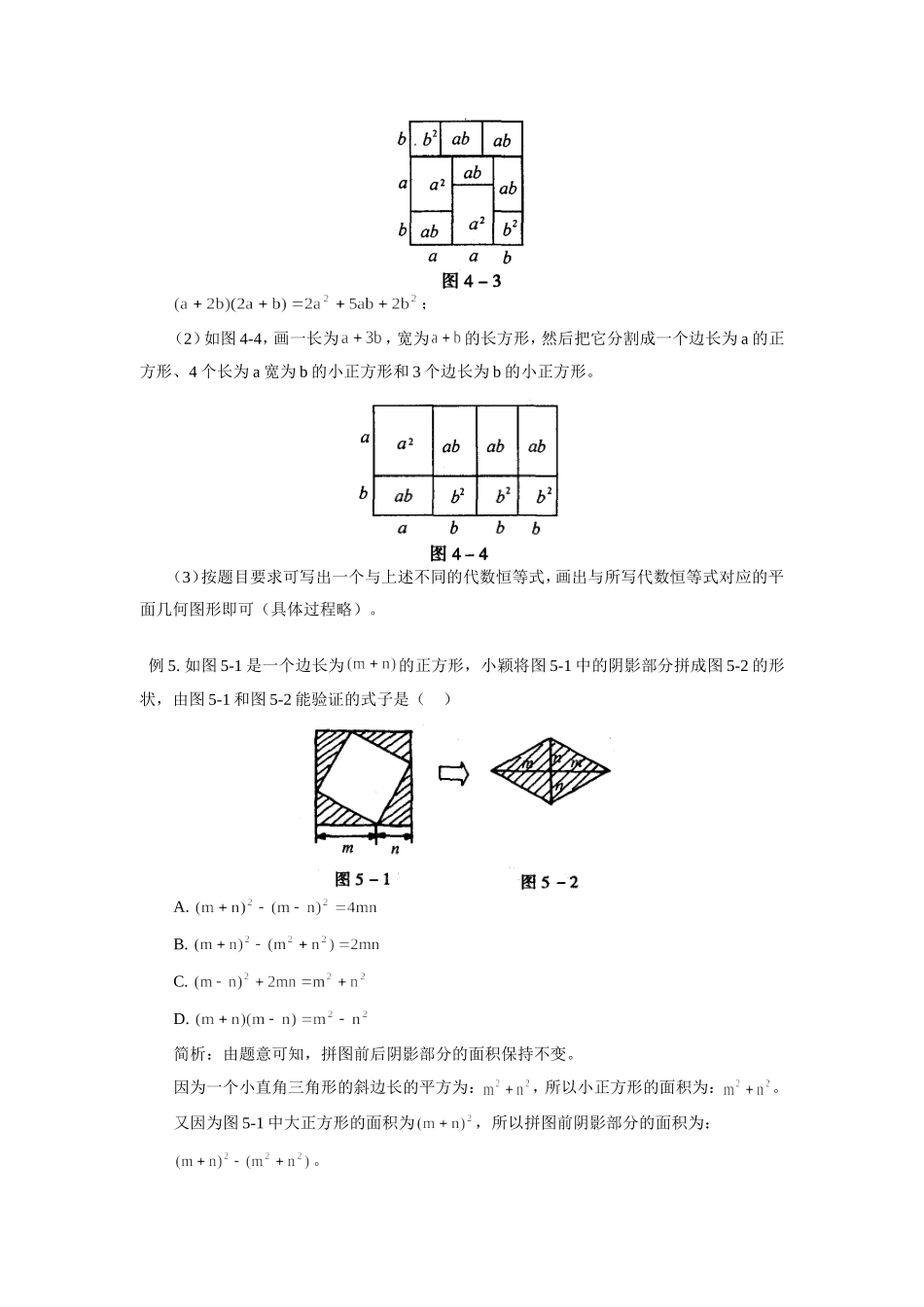
初中数学数形结合验证代数恒等式学法指导赵军数形结合思想就是将数(量)与形(图)结合起来解决问题的一种数学思想。我国著名数学家华罗庚曾说过:“数缺形时少直观,形少数时难入微;数形结合百般好,隔离分家万事休”,可见数形结合对解题的重要性。如何从一个图形中挖掘提炼一个抽象的代数恒等式,用图形来展示代数式的几何意义,体现数形结合的思想呢?下面列举几例,供大家参考。一、验证平方差公式例l.从边长为a的大正方形纸板中挖去一个边长为b的小正方形纸板后,将其裁成四个相同的等腰梯形(如图l-l),然后拼成一个平行四边形(如图l-2)。那么通过计算两个图形阴影部分的面积,可以验证成立的公式为____________。简析:从边长为a的大正方形纸板中挖去一个边长为b的小正方形,则图1-1阴影部分的面积为;每个等腰梯形的高为:;每个等腰梯形的面积为:。因为两个图形中阴影部分的面积相等所以,所以验证成立的公式为:。例2.如图2,在边长为a的正方形中剪去一个边长为b的小正方形,然后将阴影部分拼成一个长方形,分别计算这两个阴影部分的面积,验证的公式是__________。简析:从边长为a的正方形中剪去一个边长为b的小正方形,则左图面积表示为;将阴影部分拼成一个长方形,则右图的面积表示为,因为这两个阴影部分的面积相等,所以,即验证的公式为:。二、验证完全平方公式例3.如图3,将边长为的正方形分割成四个部分:两个边长分别为a和b的正方形、长为a宽为b的两个长方形,请你分别计算分割前和分割后的图形的面积,写出一个代数恒等式:___________。简析:利用分割前与分割后的图形面积相等的关系,可列出。所以代数恒等式为。三、验证其它代数恒等式例4.阅读材料并解答问题:我们已经知道,完全平方公式可以用平面几何图形的面积来表示,实际上还有一些代数恒等式也可以用这种形式表示,例如:就可以用图4-1或图4-2等图形的面积表示。(1)请写出图4-3所表示的代数恒等式____________。(2)试画出一个几何图形,使它的面积能表示。(3)请仿照上述方法另写一个含有的代数恒等式,并画出与之对应的几何图形。简析:(1)仿照例题,结合图4-3可知:;(2)如图4-4,画一长为,宽为的长方形,然后把它分割成一个边长为a的正方形、4个长为a宽为b的小正方形和3个边长为b的小正方形。(3)按题目要求可写出一个与上述不同的代数恒等式,画出与所写代数恒等式对应的平面几何图形即可(具体过程略)。例5.如图5-1是一个边长为的正方形,小颖将图5-1中的阴影部分拼成图5-2的形状,由图5-1和图5-2能验证的式子是()A.B.C.D.简析:由题意可知,拼图前后阴影部分的面积保持不变。因为一个小直角三角形的斜边长的平方为:,所以小正方形的面积为:。又因为图5-1中大正方形的面积为,所以拼图前阴影部分的面积为:。因为拼图后形成的菱形(即图5-2)的面积为:,所以。故选(B)。