初中数学锐角三角函数精析精练全国通用 试题VIP免费

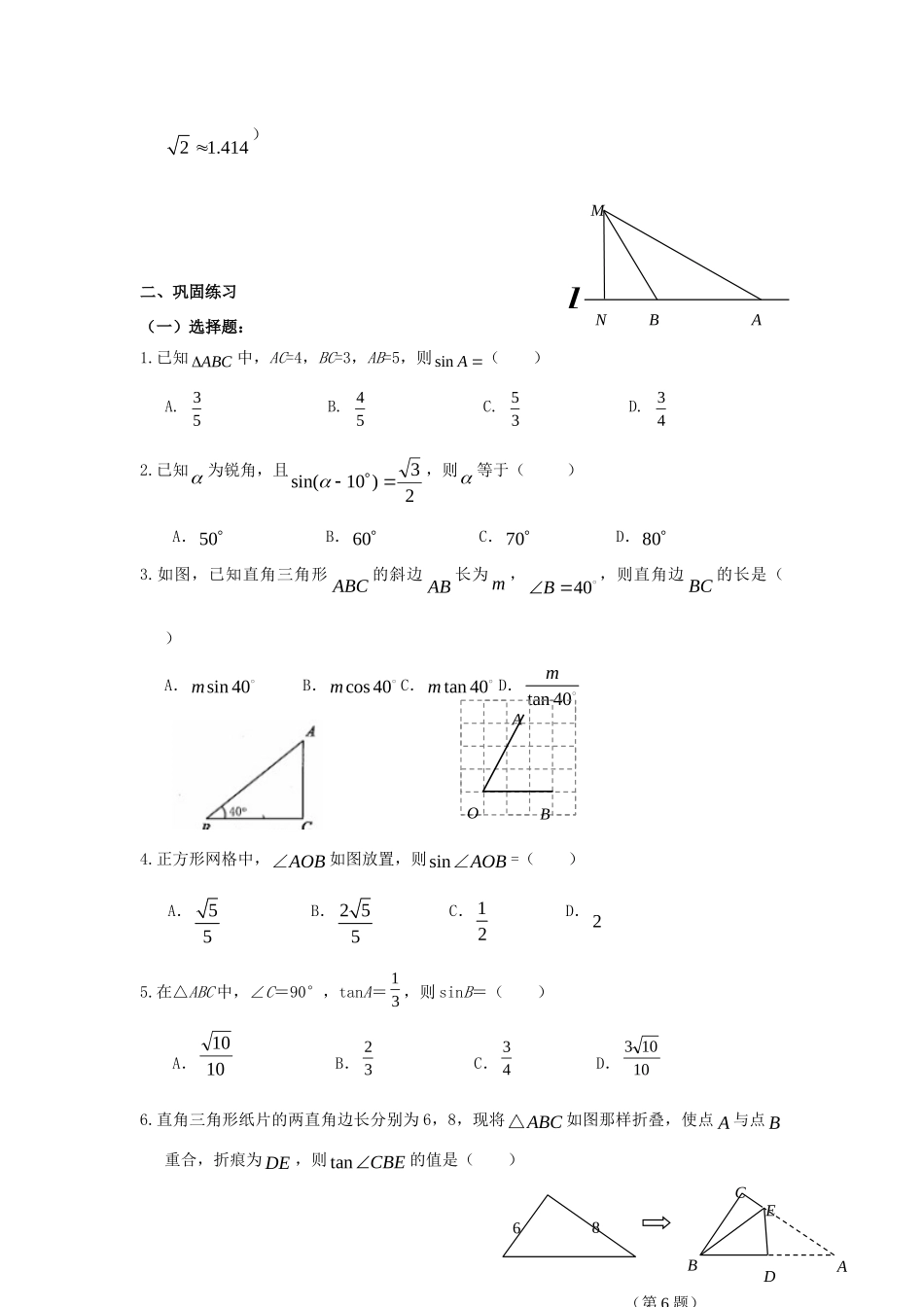
ACB锐角三角函数精析精练一、知识梳理1.三角函数的概念：在Rt△ABC中，∠C=90，SinA=斜边的对边A，cosA=斜边的邻边A，tanA=的邻边的对边AA例1：已知在RtABC△中，∠C为直角，AC=4cm，BC=3cm，sin∠A=．例2：在RtABC△中，90C°，abc，，分别是ABC，，的对边，若2ba，则tanA．例3：如图1，在Rt△ABC中，∠C＝90°，AB＝5，AC＝2，则cosA的值是（）A．B．C．D．图1图2例4：如图2，在△ABC中，∠C＝90°，AB＝10cm，sinA＝54，则BC的长为___cm.例5：正方形网格中，AOB∠如图3放置，则cosAOB∠的值为（）Ａ．55Ｂ．255Ｃ．12Ｄ．22.特殊角的三角函数值：304560Sinα212223Cosα232221tanα3313ABO图3度数三角函数例6：若30∠，则∠的余角是°，cos．例7：如果a是等腰直角三角形的一个锐角，则tan的值是（）Ａ．12Ｂ．22Ｃ．1Ｄ．2例8：45cos45sin的值等于（）A.2B.213C.3D.1例9：因为1sin302，1sin2102，所以sin210sin(18030)sin30；因为2sin452，2sin2252，所以sin225sin(18045)sin45，由此猜想，推理知：一般地当为锐角时有sin(180)sin，由此可知：sin240（）A．12B．22C．32D．33.锐角三角函数的应用例10：《中华人民共和国道路交通管理条理》规定：“小汽车在城市街道上的行驶速度不得超过70千米/时．”如图所示，已知测速站M到公路l的距离MN为30米，一辆小汽车在公路l上由东向西行驶，测得此车从点A行驶到点B所用的时间为2秒，并测得60AMN，30BMN．计算此车从A到B的平均速度为每秒多少米（结果保留两个有效数字），并判断此车是否超过限速．（参考数据：31.732，21.414）二、巩固练习（一）选择题：1.已知ABC中，AC=4，BC=3，AB=5，则sinA（）A.35B.45C.53D.342.已知为锐角，且23)10sin(，则等于（）A．50B．60C．70D．803.如图，已知直角三角形ABC的斜边AB长为m，40B，则直角边BC的长是（）A．sin40mB．cos40mC．tan40mD．tan40m4.正方形网格中，AOB∠如图放置，则sinAOB∠=（）A．55B．255C．12D．25.在△ABC中，∠C＝90°，tanA＝31，则sinB＝（）A．1010B．32C．43D．101036.直角三角形纸片的两直角边长分别为6，8，现将ABC△如图那样折叠，使点A与点B重合，折痕为DE，则tanCBE的值是（）MNBAlABO68CEABD（第6题）A．247B．73C．724D．137.如图，在高楼前D点测得楼顶的仰角为30，向高楼前进60米到C点，又测得仰角为45，则该高楼的高度大约为（）A.82米B.163米C.52米D.70米（二）填空题：8.如图，∠1的正切值等于__________．9．如图，小鸣将测倾器安放在与旗杆AB底部相距6m的C处，量出测倾器的高度CD＝1m，测得旗杆顶端B的仰角＝60°，则旗杆AB的高度为．（计算结果保留根号）10.如图，小明在楼顶A处测得对面大楼楼顶点C处的仰角为52°，楼底点D处的俯角为13°．若两座楼AB与CD相距60米，则楼CD的高度约为米．（结果保留三个有效数字）（sin130.2250≈，cos130.9744≈，tan130.2309≈，sin520.7880≈，cos520.6157≈，tan521.2799≈）11.如图，在Rt△ABC中，∠CAB=90°，AD是∠CAB的平分线，tanB=21，则CD∶DB=.（三）解答题：12.如图，某边防巡逻队在一个海滨浴场岸边的A点处发现海中的B点有人求救，便立即派三名救生员前去营救．1号救生员从A点直接跳入海中；2号救生员沿岸边(岸边看成是直线)向前跑到C点，再跳入海中；3号救生员沿岸边向前跑30O米到离B点最近（第7题）4530BADC1231231OxyDBC1352A60米的D点，再跳人海中．救生员在岸上跑的速度都是6米／秒，在水中游泳的速度都是2米／秒．若∠BAD=45°，∠BCD=60°，三名救生员同时从A点出发，请说明谁先到达营救地点B．(参考数据2≈1.4，3≈1.7)13.如图13，某数学兴趣小组在活动课上测量学校旗杆高度．已知小明的眼睛与地面的距离()AB是1.7m，看旗杆顶部M的仰角为45；小红的眼睛与地面的距离()CD是1.5m，看旗杆顶部M的仰角为30．两人相距28米且位于旗杆两侧（点BND，，在同一条直线上）．请...