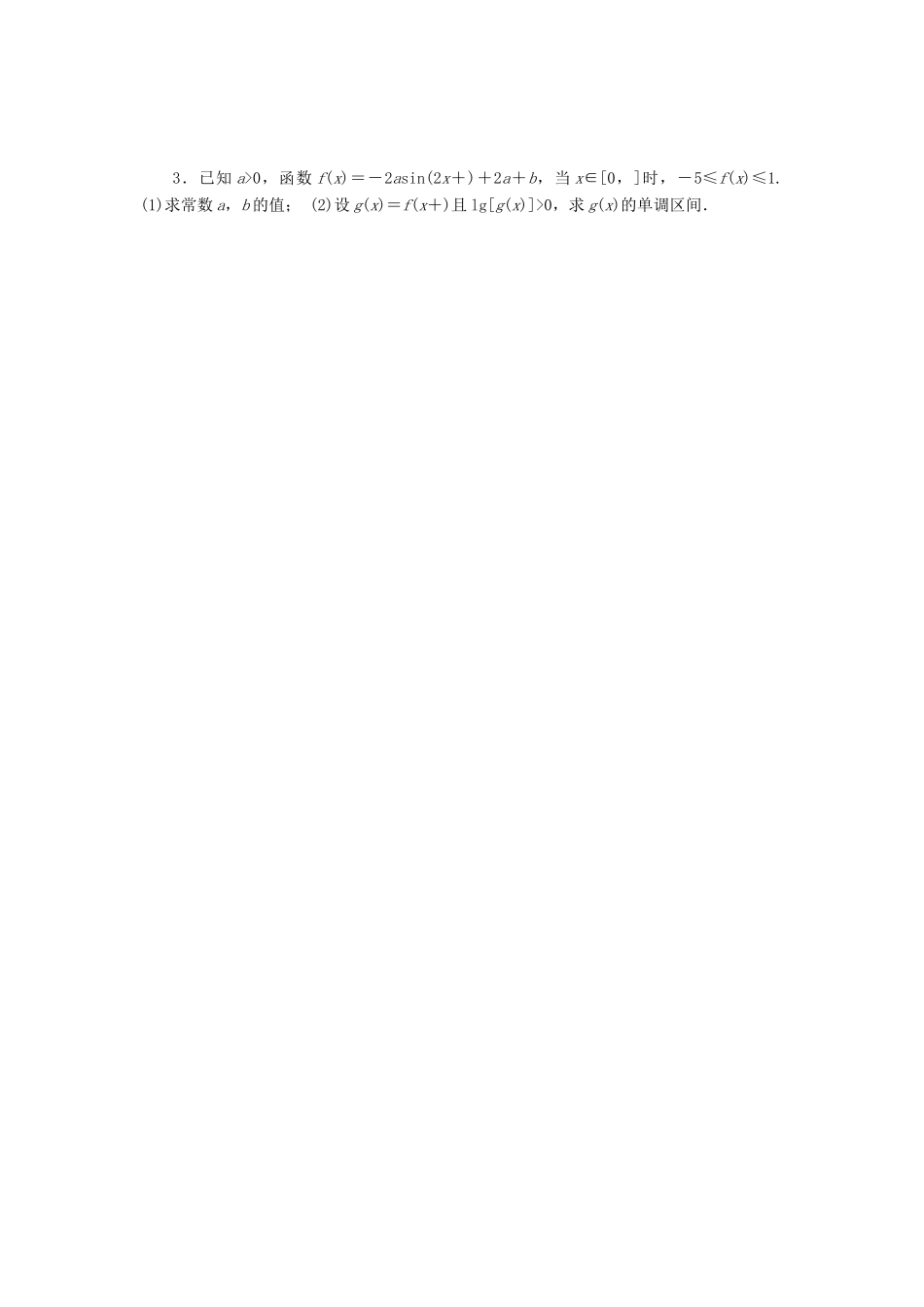
第五章三角函数、解三角形第五节:三角函数的图象与性质(第3课时)一、基础题1.函数y=2sin(0≤x≤9)的最大值与最小值之和为()A.2-B.0C.-1D.-1-2.直线x=,x=都是函数f(x)=sin(ωx+φ)(ω>0,-π<φ≤π)的对称轴,且函数f(x)在区间上单调递减,则()A.ω=6,φ=B.ω=6,φ=-C.ω=3,φ=D.ω=3,φ=-3.若函数f(x)=sin(φ∈[0,2π])是偶函数,则φ=()A.B.C.D.4.同时具有下列性质:“①对任意x∈R,f(x+π)=f(x)恒成立;②图象关于直线x=对称;③在[-,]上是增函数”的函数可以是()A.f(x)=sin(+)B.f(x)=sin(2x-)C.f(x)=cos(2x+)D.f(x)=cos(2x-)5.若函数y=2cosωx在区间[0,]上递减,且有最小值1,则ω的值可以是()A.2B.C.3D.6.如果函数y=3cos(2x+φ)的图象关于点(,0)中心对称,那么|φ|的最小值为()A.B.C.D.7.函数y=2sin(-2x)(x∈[0,π])的增区间是()A.[0,]B.[,]C.[,]D.[,π]二、中档题1.已知函数f(x)=Asin(ωx+φ)+1(ω>0,A>0,0<φ<)的周期为π,f()=+1,且f(x)的最大值为3.(1)写出f(x)的表达式;(2)写出函数f(x)的对称中心,对称轴方程.2.设函数f(x)=sin(-)-2cos2.(1)求y=f(x)的最小正周期及单调递增区间;(2)若函数y=g(x)与y=f(x)的图象关于直线x=2对称,求当x∈[0,1]时,函数y=g(x)的最大值.3.已知a>0,函数f(x)=-2asin(2x+)+2a+b,当x∈[0,]时,-5≤f(x)≤1.(1)求常数a,b的值;(2)设g(x)=f(x+)且lg[g(x)]>0,求g(x)的单调区间.