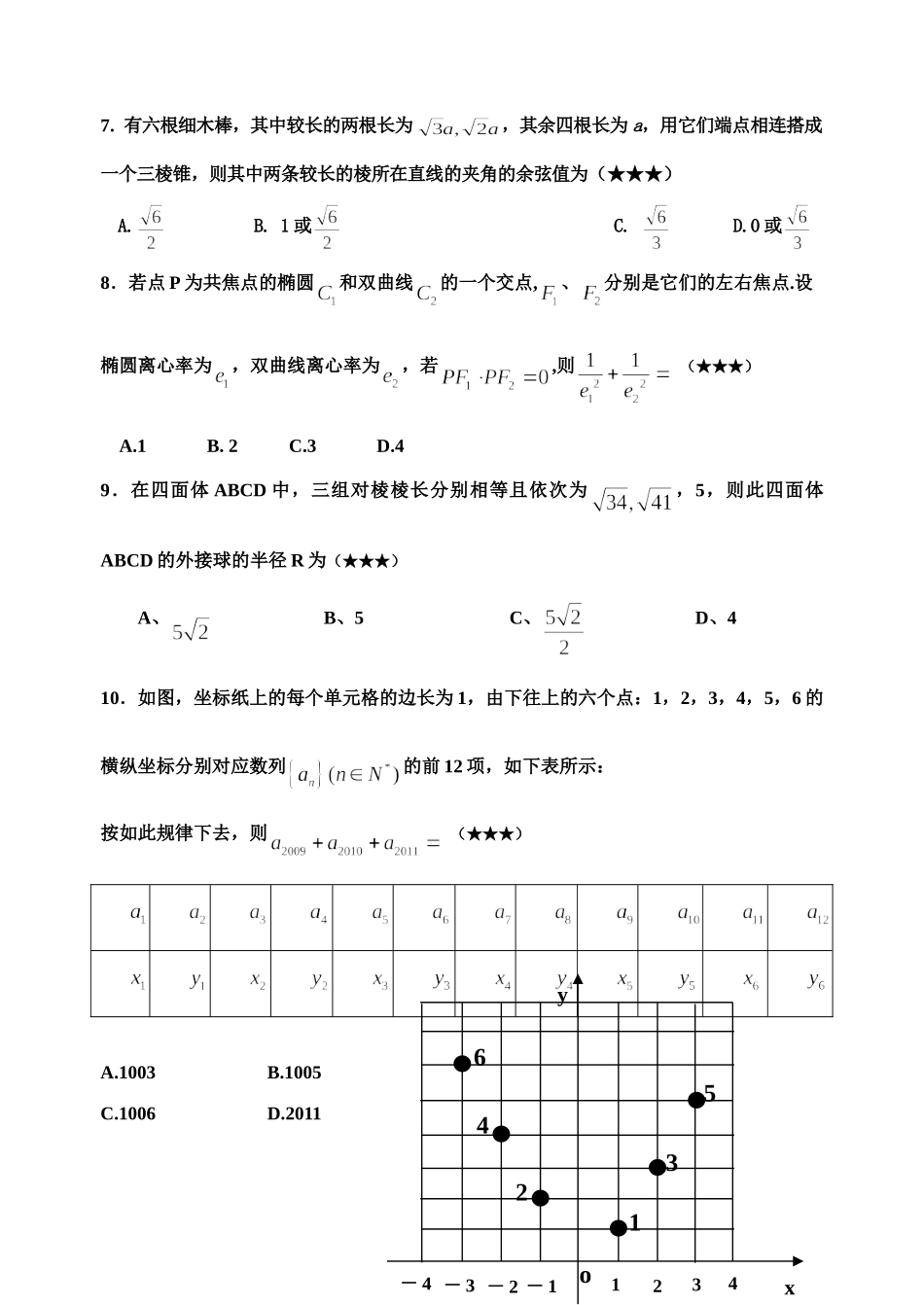
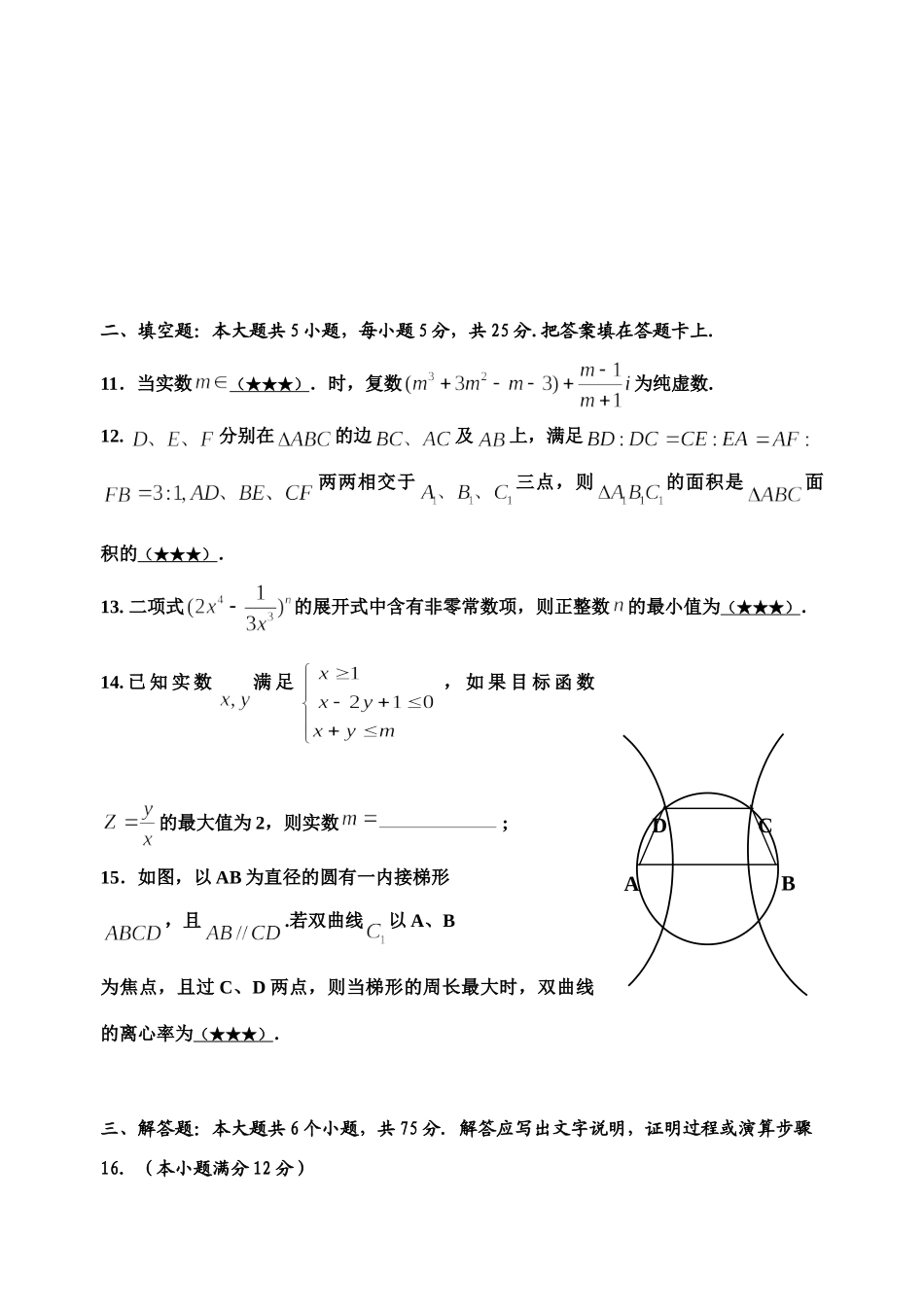
孝昌二中理科数学知识·数学能力检测卷(十二)★祝考试顺利★一、选择题:本大题共10小题,每小题5分,共50分.1.复数满足方程:,则=(★★★)A、B、C、D、2.已知全集集合则(★★★)A.B.C.D.3.函数的反函数为(★★★)A.B.C.D.4.若且则是的(★★★)A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件5.在中,,,则的值是(★★★)A.B.C.3D.96.已知函数,则对于任意实数、的值(★★★)A.恒大于0B.恒等于0C.恒小于0D.符号不确定7.有六根细木棒,其中较长的两根长为,其余四根长为a,用它们端点相连搭成一个三棱锥,则其中两条较长的棱所在直线的夹角的余弦值为(★★★)A.B.1或C.D.0或8.若点P为共焦点的椭圆和双曲线的一个交点,、分别是它们的左右焦点.设椭圆离心率为,双曲线离心率为,若,则(★★★)A.1B.2C.3D.49.在四面体ABCD中,三组对棱棱长分别相等且依次为,5,则此四面体ABCD的外接球的半径R为(★★★)A、B、5C、D、410.如图,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横纵坐标分别对应数列的前12项,如下表所示:按如此规律下去,则(★★★)A.1003B.1005C.1006D.2011-4xy-3-2-13214o325416二、填空题:本大题共5小题,每小题5分,共25分.把答案填在答题卡上.科网11.当实数(★★★).时,复数为纯虚数.12.分别在的边及上,满足两两相交于三点,则的面积是面积的(★★★).13.二项式的展开式中含有非零常数项,则正整数的最小值为(★★★).14.已知实数满足,如果目标函数的最大值为2,则实数;15.如图,以AB为直径的圆有一内接梯形,且.若双曲线以A、B为焦点,且过C、D两点,则当梯形的周长最大时,双曲线的离心率为(★★★).三、解答题:本大题共6个小题,共75分.解答应写出文字说明,证明过程或演算步骤16.(本小题满分12分)DCBA向量函数图象上相邻两个对称轴间的距离为时,函数的最小值为0.(Ⅰ)求函数的表达式;(Ⅱ)在△ABC中,若的值.17.(本小题满分12分)如图,已知正三棱柱—的底面边长是,是侧棱的中点,直线与侧面所成的角为.(Ⅰ)求此正三棱柱的侧棱长;(Ⅱ)求二面角的大小;(Ⅲ)求点到平面的距离.18.(本小题满分12分)有10张形状、大小相同的卡片,其中2张上写着数字,另外5张上写着数字1,余下3张上写着数字2。从中随机地取出1张,记下它的数字后放回原处。当这种手续重复进行2次时,为所记下的两个数之和。(1)求=2时的概率;(2)求的数学期望;19.(本小题满分12分)已知点、和动点满足:,ABCD1A1B1C且存在正常数,使得(I)求动点的轨迹的方程;(II)设直线与曲线相交于两点、,且与轴的交点为.若求的值.20.21.(本小题满分14分)(1)求证:当时,不等式对于恒成立.(2)对于在(0,1)中的任一个常数,问是否存在使得成立?如果存在,求出符合条件的一个;否则说明理由。网孝昌二中理科数学知识·数学能力检测卷(十二)参考答案CDDCAACBCB11.-312.4/13;13.714.315.16.解:(1)依题意,(2)又在Rt△ABC中,又17解:(Ⅰ)设正三棱柱—的侧棱长为.取中点,连.是正三角形,.又底面侧面,且交线为.侧面.连,则直线与侧面所成的角为.在中,,解得,此正三棱柱的侧棱长为.(Ⅱ)解法1:过作于,连,侧面.为二面角的平面角.在中,,又,.又在中,.故二面角的大小为.(Ⅲ)解法1:由(Ⅱ)可知,平面,平面平面,且交线为,过作于,则平面.在中,.为中点,点到平面的距离为.解法2:(思路)取中点,连和,由,易得平面平面,且交线为.过点作于,则的长为点到平面的距离.解法3:(思路)等体积变换:由可求.题(Ⅱ)、(Ⅲ)的向量解法:(Ⅱ)解法2:如图,建立空间直角坐标系.则.设为平面的法向量.由得.取又平面的一个法向量.结合图形可知,二面角的大小为.(Ⅲ)解法4:由(Ⅱ)解法2,点到平面的距离=.18.解:(1)卡片的出法有(0,0),(0,1),(1,0),(0,2),(2,0),(1,1),(1,2),(2,1),(2,2)共9种而=2时,出现三种(0,2),(2,0),(1,1)故………(6分)(2)同(1)处理方法可求,,,因此,的数学期望………………………………(12分)19.解:...