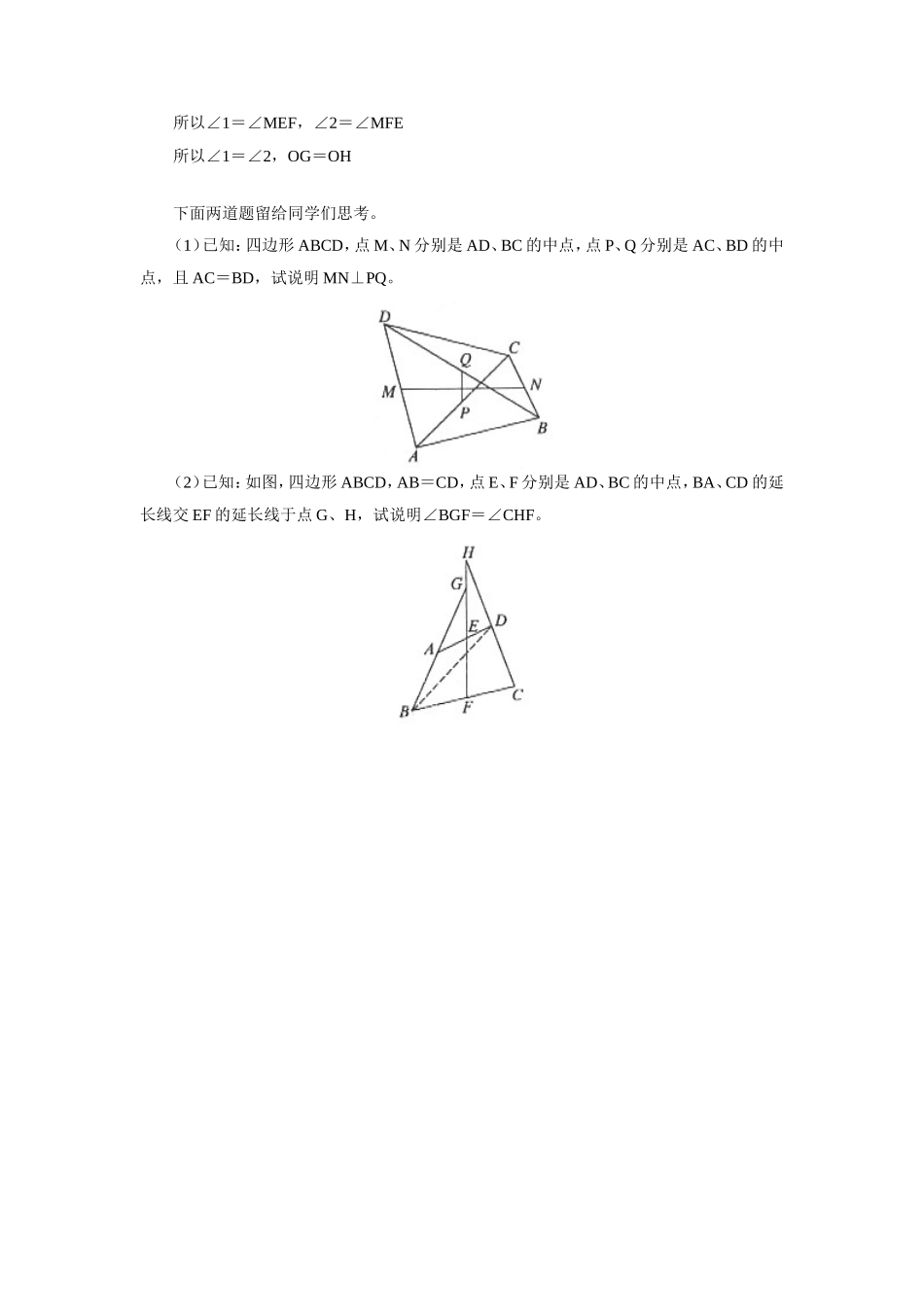
三角形的中位线用于解四边形问题江舜华单纯的三角形中位线问题并不复杂,但把它放到四边形中就难多了。下面通过一些例子来有序地讨论这些问题。例1.已知点E、F、G、H分别是四边形ABCD四边的中点,试问四边形EFGH是平行四边形吗?分析:这是个引子问题,也是个基础问题。只要连结四边形ABCD的一条对角线,再利用三角形中位线性质和平行四边形的判定定理“一组对边平行且相等的四边形是平行四边形”可解决问题。它也有许多引伸。如:当四边形ABCD满足什么样条件时,连结它四边中点所得到的四边形是菱形?答案是对角线相等。想想为什么?例2.已知:如图,在△ABC中,点D、E、F分别是三边AB、BC、AC的中点,AH是BC边上的高,垂足是H,试说明四边形DHEF是等腰梯形。分析:这是一道三角形的中位线与直角三角形斜边上的中线的性质巧妙结合的题。同时,如何描述一下四边形是等腰梯形也是很难的。解:因为点D、E、F分别是AB、BC、AC的中点,所以,DF∥BC又因为HE<BE,所以HE<DF所以四边形DHEF是梯形。又,且AH⊥BC所以,则DH=EF所以四边形DHEF是等腰梯形。例3.已知:如图,四边形ABCD,点E、F分别是AB、CD的中点,试说明。分析:本题看条件很简单,如何得结论似乎无处入手。但只要想到三角形中位线,知道构造三角形,这问题也不难。解:连结BD,取BD中点为H,连结EH、FH。因为点E、F分别是AB、CD的中点所以又,所以即例4.已知:如图,四边形ABCD,AC、BD交于点O,且AC=BD,点E、F分别是AB、CD中点,连结EF交AC、BD于G、H,试说明OG=OH。分析:本题看条件比例3多了一个条件,但解题仍比较困难,这时经验与想象力就很重要了。解:取BC中点为M,连结ME、MF因为点E、F分别是AB、CD的中点所以ME∥AC,MF∥BD又AC=BD,所以ME=MF则∠MEF=∠MFE又ME∥AC,MF∥BD所以∠1=∠MEF,∠2=∠MFE所以∠1=∠2,OG=OH下面两道题留给同学们思考。(1)已知:四边形ABCD,点M、N分别是AD、BC的中点,点P、Q分别是AC、BD的中点,且AC=BD,试说明MN⊥PQ。(2)已知:如图,四边形ABCD,AB=CD,点E、F分别是AD、BC的中点,BA、CD的延长线交EF的延长线于点G、H,试说明∠BGF=∠CHF。