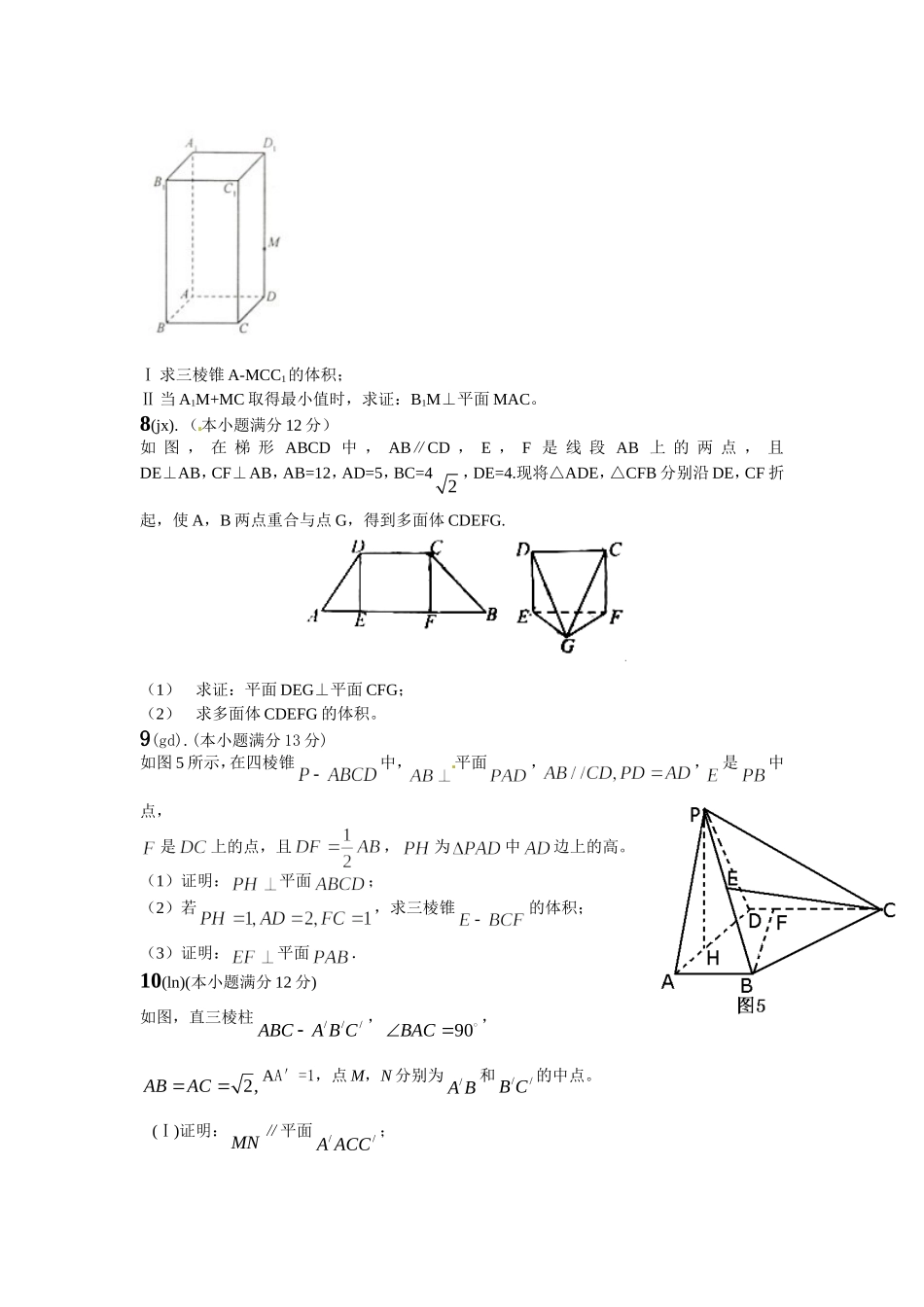
立体几何高考专题训练1.(bj)(本小题共14分)如图1,在Rt△ABC中,∠C=90°,D,E分别为AC,AB的中点,点F为线段CD上的一点,将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图2。(1)求证:DE∥平面A1CB;(2)求证:A1F⊥BE;(3)线段A1B上是否存在点Q,使A1C⊥平面DEQ?说明理由。2(hn).(本小题满分12分)如图6,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是等腰梯形,AD∥BC,AC⊥BD。(Ⅰ)证明:BD⊥PC;[来源:学科网ZXXK](Ⅱ)若AD=4,BC=2,直线PD与平面PAC所成的角为30°,求四棱锥P-ABCD的体积。3(sx).(本小题满分12分)直三棱柱ABC-A1B1C1中,AB=AA1,=[来源:学+科+网](Ⅰ)证明;[来源:Zxxk.Com](Ⅱ)已知AB=2,BC=,求三棱锥的体积4.(qg)(本小题满分12分)如图,三棱柱中,侧棱垂直底面,∠ACB=90°,AC=BC=AA1,D是棱AA1的中点。(I)证明:平面⊥平面(Ⅱ)平面分此棱柱为两部分,求这两部分体积的比.5.(js)(本小题满分14分)如图,在直三棱柱中,,分别是棱上的点(点D不同于点C),且为的中点.求证:(1)平面平面;(2)直线平面ADE.6(sh).如图,在三棱锥P-ABC中,PA⊥底面ABC,D是PC的中点.已知∠BAC=,AB=2,AC=2,PA=2.求:(1)三棱锥P-ABC的体积;(6分)(2)异面直线BC与AD所成的角的正弦值.(6分)7.(fj)(本小题满分12分)如图,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M为棱DD1上的一点。FEPABCDⅠ求三棱锥A-MCC1的体积;Ⅱ当A1M+MC取得最小值时,求证:B1M⊥平面MAC。8(jx).(本小题满分12分)如图,在梯形ABCD中,AB∥CD,E,F是线段AB上的两点,且DE⊥AB,CF⊥AB,AB=12,AD=5,BC=42,DE=4.现将△ADE,△CFB分别沿DE,CF折起,使A,B两点重合与点G,得到多面体CDEFG.(1)求证:平面DEG⊥平面CFG;(2)求多面体CDEFG的体积。9(gd).(本小题满分13分)如图5所示,在四棱锥中,平面,,是中点,是上的点,且,为中边上的高。(1)证明:平面;(2)若,求三棱锥的体积;(3)证明:平面.10(ln)(本小题满分12分)如图,直三棱柱///ABCABC,90BAC,2,ABACAA′=1,点M,N分别为/AB和//BC的中点。(Ⅰ)证明:MN∥平面//AACC;(Ⅱ)求三棱锥/AMNC的体积。(锥体体积公式V=13Sh,其中S为底面面积,h为高)11(tj).(本小题满分13分)如图,在四棱锥P-ABCD中,底面ABCD是矩形,AD⊥PD,BC=1,PC=2,PD=CD=2.(I)求异面直线PA与BC所成角的正切值;(II)证明平面PDC⊥平面ABCD;(III)求直线PB与平面ABCD所成角的正弦值。12(cq).(本小题满分12分,(Ⅰ)小问4分,(Ⅱ)小问8分)如图(20),在直三棱柱ABC-A1B1C1中,AB=4,AC=BC=3,D为AB的中点。(Ⅰ)求异面直线CC1和AB的距离;(Ⅱ)若AB1⊥A1C,求二面角A1—CD—B1的平面角的余弦值。13(sc)、(本小题满分12分)如图,在三棱锥中,,,,点在平面内的射影在上。(Ⅰ)求直线与平面所成的角的大小;(Ⅱ)求二面角的大小。ABCP