数学归纳法1VIP免费

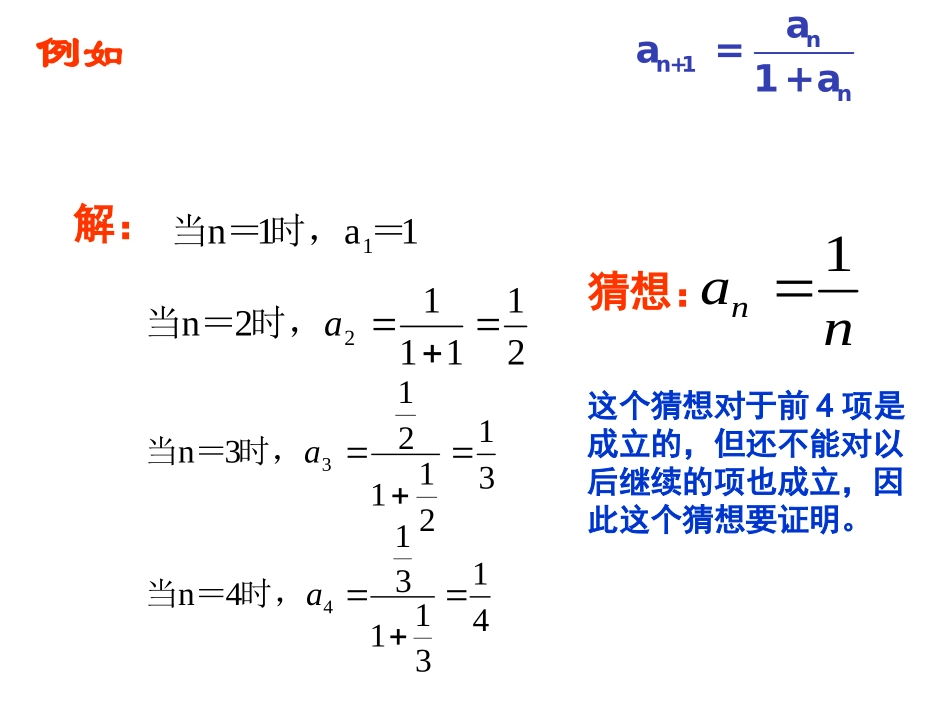
数学归纳法数学归纳法（（11））数学归纳法数学归纳法（（11））宁乡一中邹学军这种由某类事物的部分对象具有某些特征,推出该类事物的全部对象都具有这些特征的推理,或者由个别事实概栝出一般结论的推理,称为归纳推理.(简称：归纳)归纳是立足于观察、经验、实验和对有限资料分析的基础上.提出带有规律性的结论.需证明一、复习：什么是归纳推理？例如已知数列{an}的第1项a1=1且(n=1,2,3…),试归纳出这个数列的通项公式.nn+1naa=1+a1a1n1＝时，＝当31211213n3a时，＝当41311314n4a时，＝当解：nan1猜想：211112n2a时，＝当这个猜想对于前4项是成立的，但还不能对以后继续的项也成立，因此这个猜想要证明。费尔马(1601.8—1665.1)，法国数学家。的数都是质数任何形如猜想于是他用归纳推理提出都是质数，)(126553712257121712512*222243212Nnn(费马猜想)670041764142949672971225522是一个合数：时，nn结论是错误的。对于某类事物，由它的一些特殊事例或其全部可能情况，归纳出一般结论的推理方法，叫归纳法。归纳法｛完全归纳法不完全归纳法由特殊一般特点:二、归纳法定义：播放视频1播放视频2已知数列{an}的第1项a1=1且(n=1,2,3…),你能否类比多米若骨牌游戏来解决你的猜想是正确的？nn+1naa=1+anan1猜想：三、什么是数学归纳法？对于某些与正整数n有关的命题常常采用下面的方法来证明它的正确性：1.先证明当n取第一个值n0时命题成立；2.然后假设当n=k(kN*，k≥n0)时命题成立，证明当n=k+1时命题也成立。这种证明方法就叫做。数学归纳法(1)第一步，是否可省略？不可以省略。(2)第二步，从n=k(k≥n0)时命题成立的假设出发，推证n=k+1时命题也成立。既然是假设，为什么还要把它当成条件呢？这一步是在第一步的正确性的基础上，证明传递性。想一想验证n=n0时命题成立若n=k(k≥n0)时命题成立,证明n=k+1时命题也成立.归纳奠基归纳递推命题对从n0开始所有的正整数n都成立用数学归纳法证明：n例1已知数列{a}为等差，公差为d,n1通项公式为a=a+(n-1)dnn-1n1已知数列{a}为等为q,求证:通项：公式为a=aqnn-1练习比数列，公比（提示：a=qa）1）第一步应做什么？此时n0=，左=，2）假设n=k时命题成立，即6)12)(1(3212222kkkk当n=k时，等式左边共有项，第k项是。kk2思考？6)12)(1(3212222nnnn112例2用数学归纳法证明Nn3）当n=k+1时，命题的形式是61)1(21)1()1()1(32122222kkkkk4）此时，左边增加的项是2)1(k5)从左到右如何变形？（1）当n=1时左边＝12＝1，右边＝163216)12)(1(3212222kkkk那么例2用数学归纳法证明Nn6)12)(1(3212222nnnn证明：（2）假设当n=k时，等式成立，就是等式成立。222222)1(6)12)(1()1(321kkkkkk222222)1(6)12)(1()1(321kkkkkk这就是说，当n=k+1时等式也成立。根据（1）和（2），可知等式对任何n∈N＊都成立。6)1(6)12)(1(2kkkk6)672)(1(2kkk6)32)(2)(1(kkk61)1(21)1()1(kkk上如证明对吗？为什么？证明：①当n=1时，左边＝1右边＝1②设n=k时，有2)12(.........531kk2)1k(2)1k](1)1k(21[]1)1k(2[)1k2(...........531即n=k+1时，命题成立。根据①②问可知，对nN∈＊，等式成立。第二步证明中没有用到假设，这不是数学归纳法证明。思考：用数学归纳法证明:当Nn2)12(..........531nn等式成立。小结小结重点：两个步骤、一个结论；注意：递推基础不可少，归纳假设要用到，结论写明莫忘掉。作业:P95练习1、2；P96A组1（3）