113导数的几何意义VIP免费

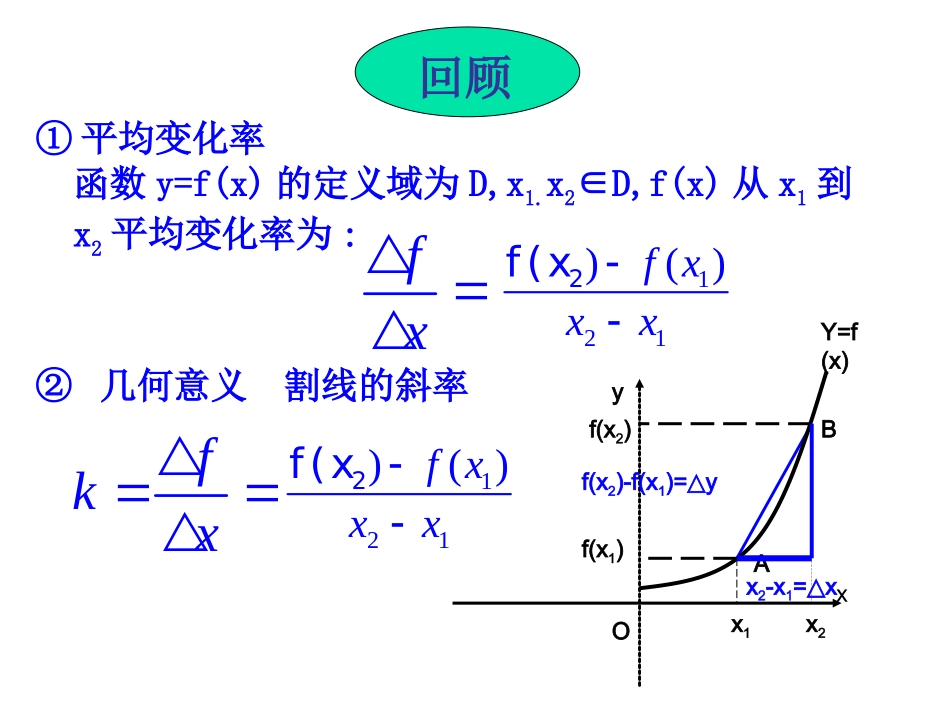
导数的几何意义学习目标：1.理解导数的几何意义。2.利用导数的几何意义解决相关问题回顾①平均变化率fx121)()fxxx2f(x函数y=f(x)的定义域为D,x1.x2∈D,f(x)从x1到x2平均变化率为:②几何意义割线的斜率OABxyY=f(x)x1x2f(x1)f(x2)x2-x1=x△f(x2)-f(x1)=y△fkx121)()fxxx2f(x回顾00000()()'(),limlimxxfxfffxxxxx(3)函数y=f(x)在x=x0处的瞬时变化率是函数y=f(x)在x=处的导数0x由导数的意义可知,求函数y=f(x)在点x0处的导数的基本步骤是:00(1)()();yfxxfx求函数的增量00()()(2);fxxfxyxx求平均变化率00(3)()lim.xyfxx取极限，得导数注意:这里的增量不是一般意义上的增量,它可正也可负.自变量的增量Δx的形式是多样的,但不论Δx选择哪种形式,Δy也必须选择与之相对应的形式.回顾一差二比三极限l2l1AB0xy直线l1与曲线C有唯一公共点B，但我们不能说l1与曲线C相切直线l2与曲线C有不止一个公共点A，我们能说l2是曲线C在点A处的切线如图直线L1是曲线的切线吗？那么对于一般的曲线，曲线切线该如何寻找呢？βy=f(x)PQMΔxΔyOxyβPy=f(x)QMΔxΔyOxy如图,曲线C是函数y=f(x)的图象,P(x0,y0)是曲线C上的任意一点,Q(x0+Δx,y0+Δy)为P邻近一点,PQ为C的割线,PM//x轴,QM//y轴,β为PQ的倾斜角..tan,,:xyyMQxMP则yx请问：是割线PQ的什么?斜率!PQoxyy=f(x)割线切线T请看当点Q沿着曲线逐渐向点P接近时,割线PQ绕着点P逐渐转动的情况.我们发现,当点Q沿着曲线无限接近点P即Δx→0时,割线PQ如果有一个极限位置PT.则我们把直线PT称为曲线在点P处的切线.导数的几何意义:函数在x0处的导数的几何意义:曲线y=f(x)在(x0,f(x0))点处的导数等于切线的斜率即:'00000()()()limlimxxfxxfxykfxxx切线这个概念:①提供了求曲线上某点切线的斜率的一种方法;②切线斜率的本质——函数在x=x0处的导数.例1:求曲线y=f(x)=x2+1在点P(1,2)处的切线方程.QPy=x2+1xy-111OMyx.2)(2lim)11(1)1(lim)1(:2020'xxxxxfkxx解因此,切线方程为y-2=2(x-1),即y=2x.（1）求出函数在点x0处的变化率，得到曲线在点(x0,f(x0))的切线的斜率。)(0xf（2）根据直线方程的点斜式写出切线方程，即).)(()(000xxxfxfy归纳:求切线方程的步骤（已知切点）无限逼近的极限思想是建立导数概念、用导数定义求函数的导数的基本思想，丢掉极限思想就无法理解导数概念。练习．求抛物线y=x2过点(1，1)的切线的斜率。解：过点(1，1)的切线斜率是f’(1)=200(1)(1)(1)1limlimxxfxfxxx0lim(2)2xx因此抛物线过点(1，1)的切线的斜率为2.例2.在曲线y=x2上过哪一点的切线1.平行于直线y=4x-52.垂直于直线2x-6y+5=0已知斜率求切点练习2、曲线上哪一点的切线与直线平行？223xy13xy：、函数在一区间上的导数：如果函数f(x)在开区间(a,b)内每一点都可导，就说f(x)在开区间(a,b)内可导．这时，对于开区间(a,b)内每一个确定的值x0，都对应着一个确定的导数f'(x0)，这样就在开区间(a,b)内构成了一个新的函数，我们把这一新函数叫做f(x)在开区间(a,b)内的导函数，简称为导数，记作即.求函数的导数的方法是:);()()1(xfxxfy求函数的增量;)()(:)2(xxfxxfxy的增量的比值求函数的增量与自变量.lim)()3(0xyxfyx求极限，得导函数说明:在这种方法中把x换x0即为求函数在点x0处的导数.（1）求出函数在点x0处的得到曲线在点(x0,f(x0))的切线的斜率。（2）根据直线方程的点斜式写出切线方程，即).)(()(000xxxfxfy2.求切线方程的步骤：小结:)(0xf即:'00000()()()limlimxxfxxfxykfxxx切线1.函数在处的导数的几何意义:0x练习题1．曲线y=x2在x=0处的（）A．切线斜率为1B．切线方程为y=2xC．没有切线D．切线方程为y=0D2．已知曲线y=2x2上的一点A(2，8)，则点A处的切线斜率为（）A．4B．16C．8D．2C3．函数y=f(x)在x=x0处的导数f’(x0)的几何意义是（）A．在点x=x0处的...