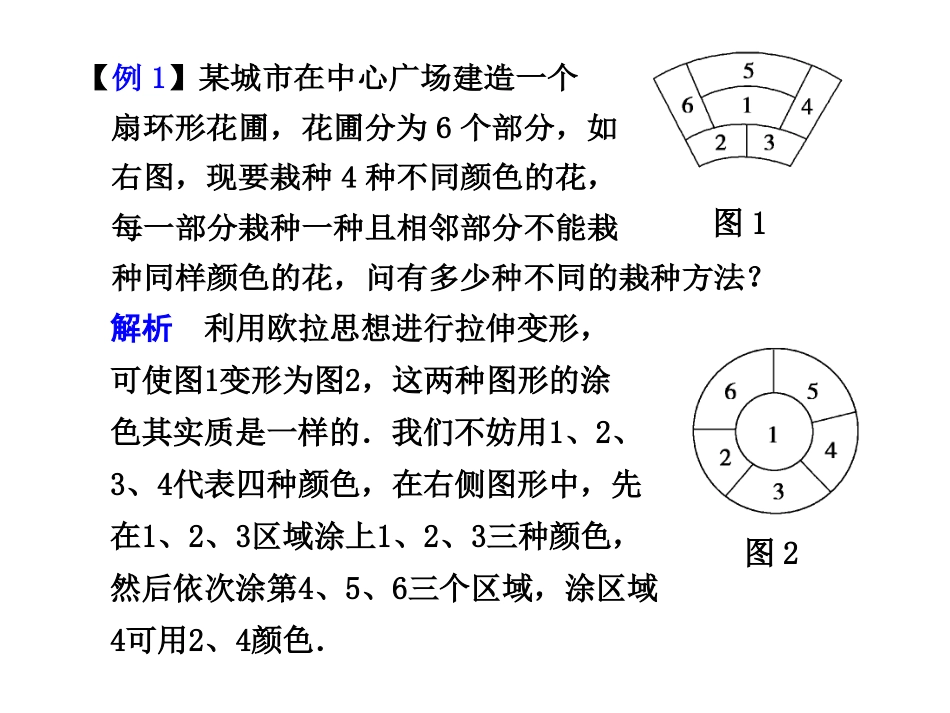
备课资讯21几何图形的涂色问题空间图形的涂色问题由于其空间位置的特点,处理问题时容易受空间想像的限制,使问题变得很不直观,若利用欧拉定理的思想与方法,通过图形的变换转化为平面图形的涂色问题,可使一类空间涂色问题得以简化而使问题变得直观.下面给出几例来看欧拉思想在涂色问题中的应用.【例1】某城市在中心广场建造一个扇环形花圃,花圃分为6个部分,如右图,现要栽种4种不同颜色的花,每一部分栽种一种且相邻部分不能栽种同样颜色的花,问有多少种不同的栽种方法?解析利用欧拉思想进行拉伸变形,可使图1变形为图2,这两种图形的涂色其实质是一样的.我们不妨用1、2、3、4代表四种颜色,在右侧图形中,先在1、2、3区域涂上1、2、3三种颜色,然后依次涂第4、5、6三个区域,涂区域4可用2、4颜色.图1图2①若区域4涂颜色2,则整个花圃有123243、123234两种涂法.②若区域4涂颜色4,则整个花圃有123434、123424、123423三种涂法.即区域1、2、3颜色确定以后,区域4、5、6有5种涂法,所以共有不同的栽种方法为A34×5=120种.【例2】将一个四棱锥的每个顶点染上一种颜色,并使同一条棱上的两端异色,如果只有5种颜色可供使用,求不同的涂色方法总数.解析本题如果将棱锥的顶点往下作投影,或者是将四棱锥看成是可以拉伸的薄膜状表面进行拉伸,变成平面图形(图1),则空间图形的涂色就能变成平面图形的涂色,继而将点扩展为平面区域,则又可变为平面内圆形区域的涂色问题(图2).方法同例1,解略.有420种涂色方法.【例3】用5种颜色给正方体ABCD—A1B1C1D1各面涂色,要求相邻两个面不同色,现已将过顶点A的3个面涂了颜色,那么其余3个面涂色方法有多少种?解析分三类,一是剩余三面的颜色与以A为顶点的三面的颜色相同,则只能涂其对面颜色,有1种涂法,二是只有2种与所涂颜色相同,则有C23种方式,另一种颜色为剩余两种颜色中的一种,故有6种涂法,三是只有一种颜色与前面所涂相同,有C13种,剩余涂为两种其它颜色,故也有6种涂法,综上有13种.【例4】现用4种颜色给三棱柱的6个顶点涂色,要求同一条棱的两端点的颜色不同,4种颜色全部用上,问有多少种不同的涂色方案?解析将左侧图形拉伸为右侧图形,则中间三点不同色,不妨为三颜色1、2、3,又4种颜色全用上,故外围三点中一定有一点涂第4种颜色,在此情况下从其余三色中任挑两色,另外两点都只有一种涂法.故共有C34A33C13C23=216种涂法.返回