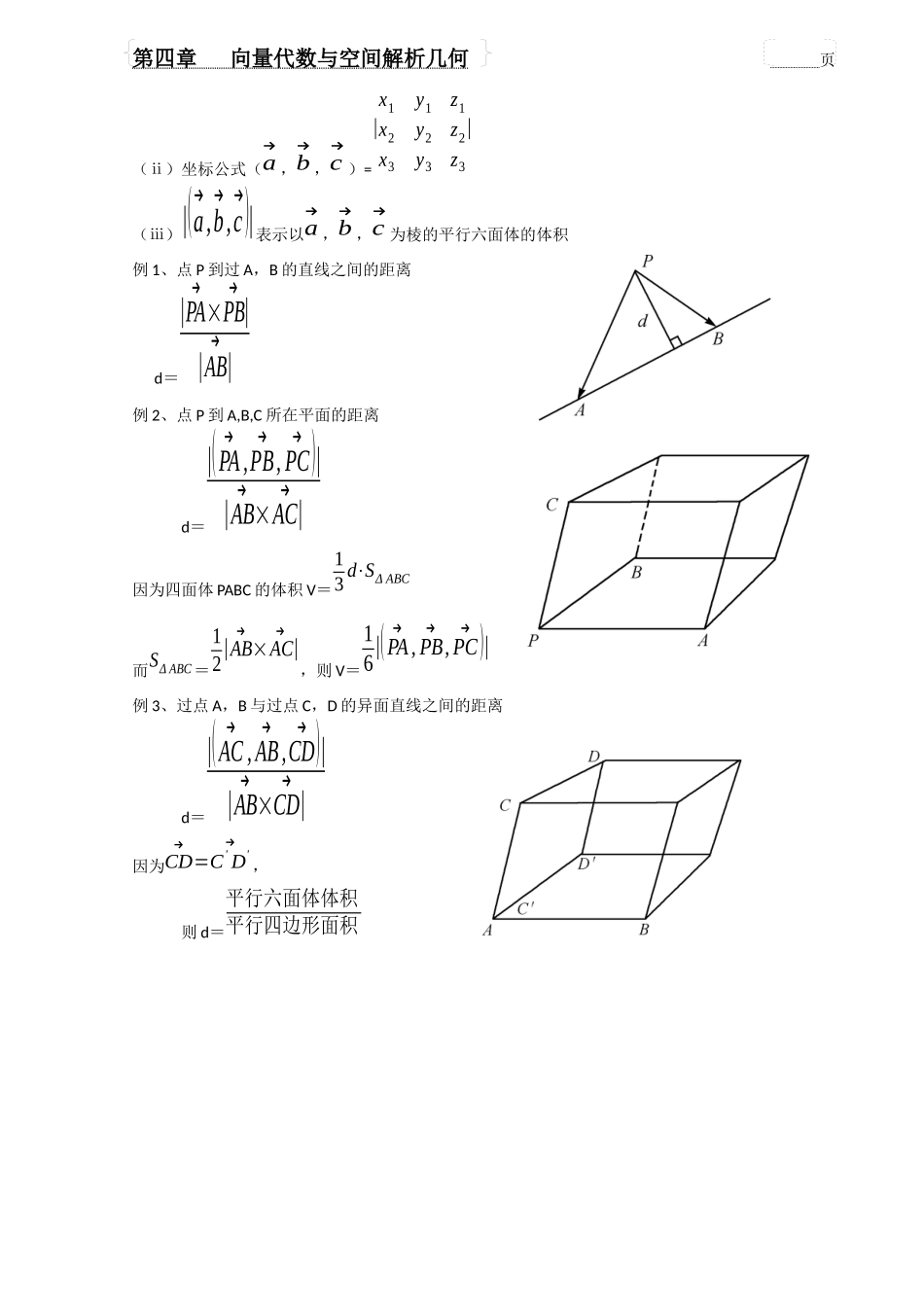
第四章向量代数与空间解析几何页第一节向量代数一、空间直角坐标系二、向量概念a→=xi→+yj→+zk→坐标(x,y,z)模|a→|=√x2+y2+z2方向角α¿¿方向余弦cosα,¿¿cosα=x√x2+y2+z2;cosβ=y√x2+y2+z2;cosγ=z√x2+y2+z2三、向量运算设a→(x1,y1,z1);b→(x2,y2,z2);c→(x3,y3,z3)1.加(减)法a→±b→=(x1±x2,y1±y2,z1±z2)2.数乘λa→=(λx1,λy1,λz1)3.数量积(点乘)(ⅰ)定义a→·b→=|a→||b→|cos∠(a→,b→)(ⅱ)坐标公式a→·b→=x1x2+y1y2+z1z2(ⅲ)重要应用a→·b→=0⇔a→¿b→4.向量积(叉乘)(ⅰ)定义|a→¿b→|=|a|→|b→|sin∠(a→,b→)a→¿b→与a→和b→皆垂直,且a→,b→,a→¿b→构成右手系(ⅱ)坐标公式a→¿b→=|i→j→k→x1y1z1x2y2z2|(ⅲ)重要应用a→¿b→=0→⇔a→,b→共线5、混合积(ⅰ)定义(a→,b→,c→)=(a→¿b→)·c→第四章向量代数与空间解析几何页(ⅱ)坐标公式(a→,b→,c→)=|x1y1z1x2y2z2x3y3z3|(ⅲ)|(a→,b→,c→)|表示以a→,b→,c→为棱的平行六面体的体积例1、点P到过A,B的直线之间的距离d=|PA→×PB→||AB→|例2、点P到A,B,C所在平面的距离d=|(PA→,PB→,PC→)||AB→×AC→|因为四面体PABC的体积V=13d⋅SΔABC而SΔABC=12|AB→×AC→|,则V=16|(PA→,PB→,PC→)|例3、过点A,B与过点C,D的异面直线之间的距离d=|(AC→,AB→,CD→)||AB→×CD→|因为CD→=C'D'→,则d=平行六面体体积平行四边形面积第四章向量代数与空间解析几何页第二节平面与直线(甲)内容要点一、空间解析几何1空间解析几何研究的基本问题。(1)已知曲面(线)作为点的几何轨迹,建立这曲面(线)的方程,(2)已知坐标x,y和z间的一个方程(组),研究这方程(组)所表示的曲面(线)。2距离公式空间两点A(x1,y1,z1)与B(x2,y2,z2)间的距离d为d=√(x2−x1)2+(y2−y1)2+(z2−z1)23定比分点公式M(x,y,z)是AB的分点:AMMB=λ,点A,B的坐标为A(x1,y1,z1),B(x2,y2,z2),则x=x1+λx21+λ,y=y1+λy21+λ,z=z1+λz21+λ当M为中点时,x=x1+x22,y=y1+y22,z=z1+z22二、平面及其方程1法(线)向量,法(线)方向数。与平面π垂直的非零向量,称为平面π的法向量,通常记成。法向量{m,n,p}的坐标称为法(线)方向数。对于给定的平面π,它的法向量有无穷多个,但它所指的方向只有两个。2点法式方程已知平面π过M(x0,y0,z0)点,其法向量={A,B,C},则平面π的方程为A(x−x0)+B(y−y0)+C(z−z0)=0或其中3一般式方程Ax+By+Cz+D=0其中A,B,C不全为零.x,y,z前的系数表示π的法线方向数,={A,B,C}是π的法向量特别情形:Ax+By+Cz=0,表示通过原点的平面Ax+By+D=0,平行于z轴的平面Ax+D=0,平行yOz平面的平面x=0表示yOz平面。第四章向量代数与空间解析几何页4三点式方程设A(x1,y1,z1),B(x2,y2,z2),C(x3,y3,z3)三点不在一条直线上。则通过A,B,C的平面方程为|x−x1y−y1z−z1x2−x1x3−x1y2−y1y3−y1z2−z1z3−z1|=05平面束设直线L的一般式方程为{A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0,则通过L的所有平面方程为K1(A1x+B1y+C1z+D1)+K2(A2x+B2y+C2z+D2)=0,其中(k1,k2)≠(0,0)6有关平面的问题两平面为π1:A1x+B1y+C1z+D1=0π2:A2x+B2y+C2z+D2=0π1与π2间夹角(ϕ)cosϕ=A1A2+B1B2+C1C2√A12+B12+C12⋅√A22+B22+C22垂直条件A1A2+B1B2+C1C2=0平行条件A1A2=B1B2=C1C2¿(¿D1D2)¿重合条件A1A2=B1B2=C1C2¿D1D2设平面π的方程为Ax+By+Cz+D=0,而点M(x1,y1,z1)为平面π外的一点,则M到平面π的距离d:d=|Ax1+By1+Cz1+D√A2+B2+C2|三直线及其方程1方向向量、方向数与直线平行的非零向量,称为直线L的方向向量,方向向量的坐标称为方向数。2直线的标准方程(对称式方程)x−x0l=y−y0m=z−z0n其中(x0,y0,z0)为直线上的点,l,¿¿为直线的方向数。3参数式方程第四章向量代数与空间解析几何页{x=x0+lty=y0+mtz=z0+nt4两点式设A(x1,y1,z1),B(x2,y2,z2)为不同的两点,则通过A和B的直线方程为x−x1x2−x1=y−y1y2−y1=z−z1z2−z15一般式方程(作为两平面的交线)6有关直线的问题两直线为L1:x−x1l1=y−y1m1=z−z1n1L2:x−x2l2=y−y2m2=z−z2n2l1l...